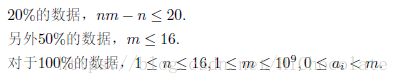2018.07.06【2018提高组】模拟B组 二分图计数
#From jzoj4196
#Description

#Input

#Output
![]()
#Sample Input
样例1
1 2
0
样例2
3 3
0
1
2
#Sample Output
样例1
1
样例2
70
首先,这题题目大意真的很难看懂,因为这图片里面很多错字。(非良心出题人)
比如:“其中”写成“集中”?
好了,不吐槽了。
题目大意(看了我好久,问别人才知道)
就是左边有n个点,右边有m个点。这些左右两边的点都是从0开始标号。
左边的点有m-1条边连向右边,也就是说只有一个点到不了。对于第i个左边的点,这个到不了的右边的点的编号就是输入中的a[i]
然后呢,我们就要从左边选出任意个点,成为一个点集合S,大小记作tot,然后这个点集合里的点就与右边的全部点二分图匹配。
设F(S)为这个二分图匹配的方案数,再设G(S)表示:2的(点集合里的点的编号)的次方的和。
什么意思?也就是一个点集合为{0,2,3,5}(编号),然后对于这个点集合
G(S)=20+22+23+25=1+4+8+32=45
然后答案就为所有点集合中的F(S)*G(S) mod (10^9+7)的和。
没那么晦涩难懂吧?不懂?再自己研究研究样例。
你说你不懂二分图匹配?一边玩去
其实这题用不到二分图匹配,看看数据就懂了。
那么怎么做呢?
#正解
首先,我们看看数据范围,发现n很小,那么就告诉我们,可以2^N的时间来枚举出当前点集合是什么,然后G就很好求了。
但是F仍然很难求,怎么办?凉拌
现在,我们来看看完全二分图的情况:
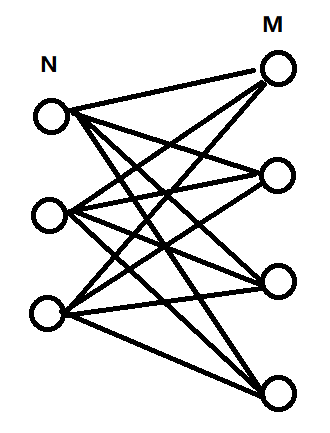
然后我们笔玩一下,推推规律,可得到满二分图的方案数就为
m * (m-1) * (m-2) * (m-3) * …… * (m-tot+1)
是不是很有意思?
但是有些点是连不到了,我们再来看看:
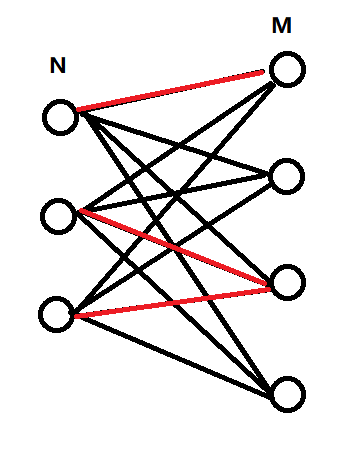
这个假设红色线不能走
然后,我们就想想如何把这些红色线的方案从答案中去掉。
然后,我们再来玩一玩,发现这个做法好像是容斥原理。
嘿嘿,那么我们就有思路了。
然后经过繁琐的摸索(因为实在是太多重复了,在此就留给读者自己思考,摸索)
我们可以总结出一个东东——
答案就为:
m(m-1)(m-2)……(m-tot+1)
-(m-1)(m-2)……(m-tot+1)*sum1
+(m-2)(m-3)……(m-tot+1)*sum2
-(m-3)(m-4)……(m-tot+1)sum3
……………………
好像有规律对吧?但是后面的这个sum是什么意思呢?
在解释这个之前,我们设一个d[]表示右边的不能被到达的点,不能到达左边的点的个数。
然后gs就表示右边不能被到达的点的个数。
有点绕,我们来看看刚才的图。
我们就可以发现,gs=2 d[]={1,2}
为什么呢?因为右边连了红色线的点的个数有两个,分别有1个左边的点与d[1]相连和2个左边的点与d[2]相连。
理解理解。
然后:
sum1=d1+d2+d3+……+dgs
sum2=d1 * d2+d1 * d3+……+d2 * d3+d2 * d4+……
sum3=d1 * d2 * d3+d1 * d2 * d4+……
然后我们脑补一下,我们就能发现这样子可以满足每次都把重复的东东给补回来或是删去。
是不是很神奇?
这个比如m(m-1)(m-2)……(m-tot+1),它除以m就代表有一个点不参与连线,然后再乘sum1那么就代表这个点与红线连线,于是就可以消出一部分方案,然后还有重复的,也就是两个点都连到同一个点,于是再加上(m-2)……(m-tot+1)乘sum2,那么又可以把一部分多删除的方案补回来,但还有重复。以此类推,然后就可以这样容斥。
但是这个sum直接暴力很难搞,于是我们来尝试优化。
我们发现:
sum2:=d1(sum1-d1)+d2(sum2-d2)+……/2
sum3:=d1(s2-d1(sum1-d1))+……/3
这里有重复的,那么我们就可以快速过。
但是还要用到逆元,因为有除数,但是考虑到模数为质数,用费马小定理即可解决。
时间复杂度(2^nn)
代码:
var
i,j,k,l,n,m,gs,tot:longint;
ans,answer,mo:int64;
a,b,c,d,e,f:array[1..16] of longint;
function qsm(x,y:int64):int64;
var
t:int64;
begin
t:=1;
while y>0 do
begin
if y and 1=1 then
t:=t*x mod mo;
x:=x*x mod mo;
y:=y shr 1;
end;
exit(t);
end;
procedure dfs(dep:longint);
var
i,j,x:longint;
l:int64;
s:array[1..16] of int64;
k:array[1..16,1..16] of longint;
begin
if (dep>n) and (tot>0) then
begin
gs:=1;
c[1]:=f[1];
fillchar(d,sizeof(d),0);
d[1]:=1;
for i:=2 to tot do
begin
j:=0;
for x:=1 to gs do
begin
if c[x]=f[i] then
begin
j:=1;
inc(d[x]);
break;
end;
end;
if j=0 then
begin
inc(gs);
c[gs]:=f[i];
d[gs]:=1;
end;
end;
ans:=0;
fillchar(s,sizeof(s),0);
for i:=1 to gs do
begin
if i=1 then
begin
for j:=1 to gs do
begin
k[i,j]:=d[j];
s[i]:=s[i]+d[j];
end;
end
else
begin
for j:=1 to gs do
begin
k[i,j]:=(d[j]*(s[i-1]-k[i-1,j])) mod mo;
s[i]:=(s[i]+k[i,j]) mod mo;
end;
s[i]:=(s[i]*qsm(i,mo-2)) mod mo;
end;
end;
l:=1;
for j:=m downto m-tot+1 do
begin
l:=(l*j) mod mo;
end;
ans:=l;
l:=l*qsm(m,mo-2) mod mo;
ans:=(ans-(s[1]*l)) mod mo;
for i:=2 to gs do
begin
l:=(l*qsm(m-i+1,mo-2)) mod mo;
if i mod 2=0 then
begin
ans:=(ans+s[i]*l+mo) mod mo;
end
else
begin
ans:=(ans-s[i]*l+mo) mod mo;
end;
end;
l:=0;
for i:=1 to tot do
begin
l:=l+b[e[i]];
end;
answer:=(answer+(l*ans) mod mo) mod mo;
end
else
if dep<=n then
begin
inc(tot);
f[tot]:=a[dep];
e[tot]:=dep;
dfs(dep+1);
f[tot]:=0;
e[tot]:=0;
dec(tot);
dfs(dep+1);
end;
end;
begin
assign(input,'bipartite.in');reset(input);
assign(output,'bipartite.out');rewrite(output);
readln(n,m);
b[1]:=1;
for i:=1 to n do
begin
if i>1 then
b[i]:=b[i-1]*2;
readln(a[i]);
inc(a[i]);
end;
j:=1;
c[1]:=a[1];
d[1]:=1;
for i:=2 to n do
begin
k:=0;
for l:=1 to i-1 do
begin
if c[l]=a[i] then
begin
k:=1;
inc(d[l]);
break;
end;
end;
if k=0 then
begin
inc(j);
c[j]:=a[i];
d[j]:=1;
end;
end;
mo:=1000000007;
gs:=j;
e[1]:=1;
f[1]:=a[1];
tot:=1;
dfs(2);
e[1]:=0;
f[1]:=0;
tot:=0;
dfs(2);
writeln(answer);
end.