【数据库基础】关系代数
文章目录
- 一、关系代数介绍
- 1. 关系代数分类
- 2. 基本的比较与逻辑运算符
- 二、集合运算Union, Difference, Intersection, Cartesian Product
- 三、关系运算
- 1. 选择运算Select
- 2. 投影运算Project
- 3. 连接运算Join
- (1). 等值连接
- (2). 自然连接Natural Join
- 4. 除法运算Divide
- 5. 实际练习【重点】
- 6. 关系代数基本运算总结【重点】
- 四、扩充的关系运算
- 1. 广义投影
- 2. 赋值
- 3. 几种外连接
- (1). 外连接
- (2). 左外连接
- (3). 右外连接
- 4. 半连接
- 5. 聚集
- 6. 外部并
- 7. 重命名
- 8. 扩充运算示例【重点】
- 五、实际练习
一、关系代数介绍
关系代数是一种抽象的查询语言,以一个或多个关系为运算对象,通过对关系进行组合和分割,得到要求的数据集合——关系。
了解基本的关系运算是学习SQL的前提,是深入学习数据库设计的前提。
1. 关系代数分类
关系代数可以分为:
- 集合运算(并、交、差;广义笛卡尔积)
- 关系运算(投影、选择、连接、除运算)
- 扩充的关系运算(广义投影、外连接、半连接、聚集等)
其中,连接、除法是比较复杂的关系运算。
2. 基本的比较与逻辑运算符
| 符号 | 含义 | L A T E X L^AT_EX LATEX |
|---|---|---|
| < \lt < | 小于 | $\lt$ |
| ≤ \leq ≤ | 小于等于 | $\leq$ |
| > \gt > | 大于 | $\gt$ |
| ≥ \geq ≥ | 大于等于 | $\geq$ |
| = = = | 等于 | $=$ |
| ≠ \neq = | 小于 | $\neq$ |
| ┐ \urcorner ┐ | 非 | $\urcorner$ |
| ∧ \wedge ∧ | 与 | $\wedge$ |
| ∨ \vee ∨ | 或 | $\vee$ |
二、集合运算Union, Difference, Intersection, Cartesian Product
集合运算将关系看作元组的集合,其运算是以关系的行为元素进行的,而关系运算不仅涉及到行,也涉及到列。
集合运算包括并、差、交、广义笛卡尔积。其中,前三者都需要参与运算的两个关系必须是相容的同类关系,它们必须有相同的列数,且对应的属性值取自同一个域(属性名可以不同)。
设: t t t 为元组变量; R R R、 S S S 为同类(同目、相应属性同域)的 n n n 元关系,下列运算的结果仍然为同类 n n n 元关系:
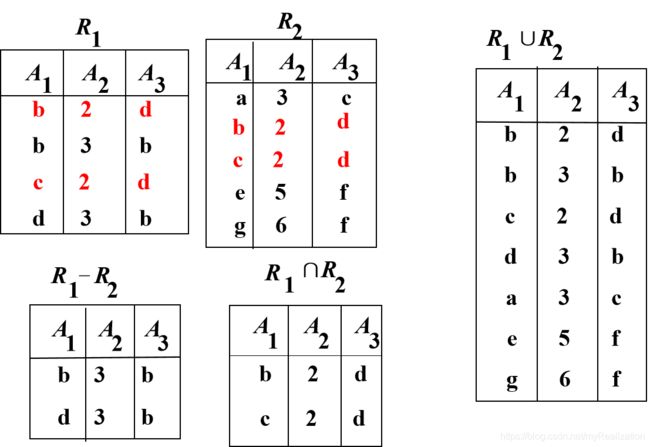
- (1)并运算: R ∪ S = { t ∣ ( t ∈ R ) ∨ ( t ∈ S ) } R∪S =\ \{\ t\ |\ (t∈R)∨(t∈S)\} R∪S= { t ∣ (t∈R)∨(t∈S)};注意:并运算不会重复出现相同的元组!
- (2)差运算: R − S = { t ∣ ( t ∈ R ) ∧ ( t ∉ S ) } R-S=\ \{\ t\ |\ (t∈R)∧(t \notin S)\} R−S= { t ∣ (t∈R)∧(t∈/S)}
- (3)交运算: R ∩ S = { t ∣ ( t ∈ R ) ∧ ( t ∈ S ) } R∩S=\ \{\ t\ |\ (t∈R)∧(t∈S)\} R∩S= { t ∣ (t∈R)∧(t∈S)}
第四种集合运算中, R R R 为 k 1 k_1 k1 元关系,有 n 1 n_1 n1 个元组; S S S 为 k 2 k_2 k2 元关系,有 n 2 n_2 n2 个元组;则广义笛卡尔积运算的结果关系为一个 k 1 + k 2 k_1+k_2 k1+k2 元的不同类新关系,有 n 1 × n 2 n_1 \times n_2 n1×n2 个元组。
- (4)积关系: R × S = { t r , t s ∣ ( t r ∈ R ) ∧ ( t s ∈ S ) } R \times S = \{\ t_r,\ t_s\ |\ (t_r \in R) \wedge (t_s \in S)\} R×S={ tr, ts ∣ (tr∈R)∧(ts∈S)}
R R R、 S S S 可以是不同类的关系,结果为不同类关系。
当需要得到一个关系 R R R 和自己的广义笛卡尔积时,必须引入 R R R 的别名,比如 R ′ R' R′,把表达式写成 R × R ′ R\times R' R×R′ 或者 R ′ × R R' \times R R′×R。运算中出现同名的属性也要同样区别。
如果是两个不同的关系 R R R 和 S S S 中存在同名的属性 A 1 A_1 A1 时,可以写成 R . A 1 R.A_1 R.A1 与 S . A 1 S.A_1 S.A1 ,其他属性同样操作。
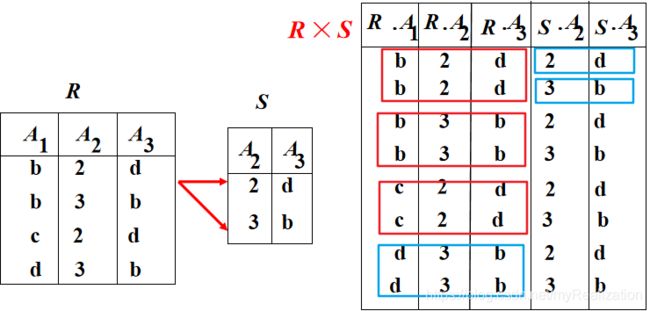
上述运算中,并、交、积运算均满足结合律,但差运算不满足结合律。其中,笛卡尔积运算是相当重要的,它是后面的条件连接、等值连接、自然连接的基础,先做笛卡尔积,然后根据条件、等值来选择元组。像自然连接不存在公共属性时,结果就是笛卡尔积,原因就在这里。同样,自然连接则是外连接、左外连接、右外连接的基础。这些都会在后面提到。
三、关系运算
在介绍关系运算前,我们引入几个记号:
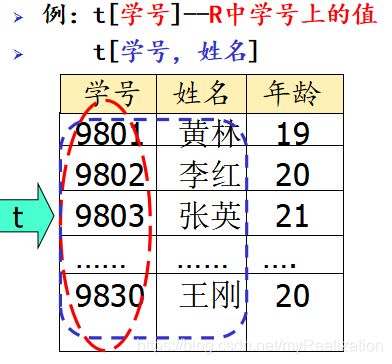
设 t t t 为 R R R 的元组变量, R ( U ) = R ( A 1 , A 2 , A 3 , . . . , A n ) R(U) = R(A_1, A_2, A_3, ..., A_n) R(U)=R(A1,A2,A3,...,An),则引入记号 t [ A ] t[A] t[A],表示关系 R R R 在 A A A 属性(组)上的所有值。例如, t [ 学 号 , 姓 名 ] t[学号, 姓名] t[学号,姓名] :表示 R R R 在学号、姓名两列上的所有属性值。
1. 选择运算Select
选择运算是在关系的行上面进行的横向筛选,结果产生同类关系。设 t t t 为 R R R 的元组变量,选择运算记作:
σ F ( R ) = { t ∣ ( t ∈ R ) ∧ F ( t ) = t r u e } \sigma_F(R) = \{\ t\ |\ (t \in R) \wedge F(t) = true\} σF(R)={ t ∣ (t∈R)∧F(t)=true}
含义: σ F ( R ) \sigma_F(R) σF(R) 表示从关系 R R R 中选择出满足 F F F 条件表达式的那些元组所构成的关系。其中, F F F 由属性名(或者直接用列号代替)、比较符、逻辑运算符构成。
例: σ A 2 > 5 ∨ A 3 ≠ “ f ” ( R ) σ_{A2\ >\ 5\ ∨\ A3\ ≠\ “f”} (R) σA2 > 5 ∨ A3 = “f”(R) 或: σ [ 2 ] > 5 ∨ [ 3 ] ≠ “ f ” ( R ) σ_{[2]\ >\ 5\ ∨\ [3]\ ≠\ “f”}(R) σ[2] > 5 ∨ [3] = “f”(R) 或者: σ [ 2 ] > 5 ∨ [ 3 ] ≠ “ f ” ( R ) σ_{[2]\ \ >\ 5\ ∨\ [3]\ ≠\ “f”}(R) σ[2] > 5 ∨ [3] = “f”(R),对下面的图来说,打勾的四行满足条件,会被选择出来构成新关系。

2. 投影运算Project
投影是在关系列上进行的纵向筛选,结果产生不同类关系,只有被选中的几列可能构成新的关系。设 t t t 为 R R R 的元组变量,投影运算记作:
∏ A ( R ) = { t [ A ] ∣ ( t ∈ R ) } \prod {}_A(R) = \{\ t[A]\ |\ (t \in R)\} ∏A(R)={ t[A] ∣ (t∈R)}
含义: ∏ A ( R ) \prod {}_A(R) ∏A(R) 表示从关系 R R R 中取出 A A A 属性指定的列,并消除重复的元组。这里的 A A A 属性可以有多个。
例: ∏ A 2 , A 3 ( R ) \prod _{A2,A3}(R) ∏A2,A3(R),关系 R R R 见上面的那幅图,结果如下:

例:对下面的学生选课表,用关系代数进行查询。
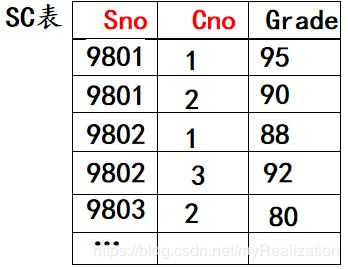
(1)查选 2 2 2 号课程的学生记录。解: σ [ 2 ] = = ′ 2 ′ ( S C ) \sigma _{[2] == '2'}(SC) σ[2]==′2′(SC)
(2)成绩在 90 90 90 分及以上的学生号。解: ∏ S n o ( σ G r a d e ≥ 90 ( S C ) ) } \prod _{Sno}(\sigma_{Grade\ \ge\ 90}(SC))\} ∏Sno(σGrade ≥ 90(SC))}
3. 连接运算Join
连接运算也被称为 θ \theta θ 连接,它是从两个关系的笛卡尔积中选择属性间满足一定条件的元组。
R ⋈ A θ B S = { t r , t s ⏞ ∣ ( t r ∈ R ) ∧ ( t s ∈ S ) ∧ ( t r [ A ] θ t s [ B ] ) } R \Join _{A\ \theta\ B} S = \{ \overbrace{t_r, t_s} \ |\ (t_r \in R) \wedge (t_s \in S) \wedge (t_r[A]\ \theta\ t_s[B]) \} R⋈A θ BS={tr,ts ∣ (tr∈R)∧(ts∈S)∧(tr[A] θ ts[B])}
上式可以用其他关系代数式表示为:
R ⋈ A θ B S = σ R . A θ S . B ( R × S ) R\Join _{A\ \theta\ B} S = \sigma _{R.A\ \theta\ S.B}\ (R \times S) R⋈A θ BS=σR.A θ S.B (R×S)
含义:从 R × S R \times S R×S 中选取—— R R R 关系在 A A A 属性组上的值与 S S S 关系在 B B B 属性组上值——满足 θ \theta θ 关系的元组,构成一个新关系。
常见的连接运算除了上面的一般条件连接外,还有下面两种:
(1). 等值连接
即 θ \theta θ 关系为 = = = 的连接,可以用其他关系代数式表示为:
R ⋈ A = B S = σ R . A = S . B ( R × S ) R \Join _{A\ =\ B} S = \sigma_{R.A = S.B}\ (R \times S) R⋈A = BS=σR.A=S.B (R×S)
(2). 自然连接Natural Join
这是一种特殊的等值连接,要求两个关系中进行比较的分量是公共的属性组,并且要去掉重复的属性!若 R R R 和 S S S 具有相同的属性组 B B B,则自然连接记作:
R ⋈ S = { t r , t s ⏞ ∣ ( t r ∈ R ) ∧ ( t s ∈ S ) ∧ ( t r [ B ] = t s [ B ] ) R \Join S = \{\overbrace {t_r, t_s}\ |\ (t_r \in R) \wedge (t_s \in S) \wedge (t_r[B] = t_s[B]) R⋈S={tr,ts ∣ (tr∈R)∧(ts∈S)∧(tr[B]=ts[B])
自然连接可以用其他关系代数式表示,设 R R R, S S S 有同名属性 B i ( i = 1 , 2 , . . . , k ) B_i\ (i = 1, 2,..., k) Bi (i=1,2,...,k),有:
R ⋈ S = ∏ 无 重 复 属 性 名 者 ( θ R . B 1 = S . B 1 ∧ . . . ∧ R . B k = S . B k ( R × S ) ) R \Join S = \prod_{无重复属性名者}\ (\theta _{R.B_1 = S.B_1\ \wedge\ ...\ \wedge\ R.B_k = S.B_k}\ (R \times S)) R⋈S=无重复属性名者∏ (θR.B1=S.B1 ∧ ... ∧ R.Bk=S.Bk (R×S))
比起一般的等值连接,自然连接有特殊要求: R R R、 S S S 有同名属性,其连接结果:满足 同名属性 值也对应相同,并且 去掉重复属性后 的连接元组集合。自然连接的运算步骤可分解为:
1. 1. 1. 计算 R × S R\times S R×S;
2. 2. 2. 选择满足等值条件 R . B 1 = S . B 1 ∧ . . . ∧ R . B k = S . B k R.B_1 = S.B_1 \wedge\ ...\ \wedge R.B_k = S.B_k R.B1=S.B1∧ ... ∧R.Bk=S.Bk 的元组;
3. 3. 3. 去掉重复属性 S . B 1 , . . . , S . B k S.B_1, ...\ , S.B_k S.B1,... ,S.Bk。
如果 R R R, S S S 无公共属性,则 R ⋈ S = R × S R \Join S = R\times S R⋈S=R×S。
等值连接与自然连接的区别:
(1)自然连接一定是等值连接,但等值连接不一定是自然连接。因为自然连接要求相等的分量必须是公共属性,而等值连接相等的分量不一定是公共属性。
(2)等值连接不要求把重复的属性去掉,而自然连接要把重复属性去掉。
例子:已知有图所示的关系 R R R, S S S如下:
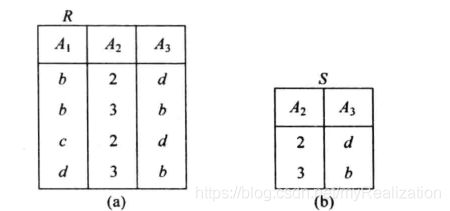
其笛卡尔积 R × S R \times S R×S 为:

(1)条件连接 R ⋈ [ 2 ] > [ 1 ] S R \Join_{[2] \gt [1]} S R⋈[2]>[1]S 示例,运算结果如下:
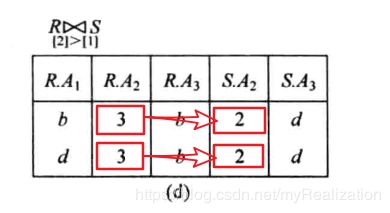
(2)等值连接 R ⋈ [ 2 ] = [ 1 ] S R\Join _{[2] = [1]} S R⋈[2]=[1]S 运算结果如下:

(3)自然连接 R ⋈ S R \Join S R⋈S 运算结果如下:

4. 除法运算Divide
设关系 R ( X , Y ) R(X,Y) R(X,Y) 与 S ( Y , Z ) S(Y, Z) S(Y,Z), X , Y , Z X,Y,Z X,Y,Z 为属性 组, X X X 属性组上的值为 x i x_i xi,除法运算记作:
R ÷ S = { t [ X ] ∣ t ∈ R ∧ ∏ Y ( S ) ⊆ Y X } R \div S = \{\ t[X]\ |\ t \in R \wedge \prod {}_Y(S) \subseteq Y_X\} R÷S={ t[X] ∣ t∈R∧∏Y(S)⊆YX}
分解 R ÷ S R\div S R÷S 的步骤如下:
1. 1. 1. 求 ∏ X ( R ) \prod {}_X(R) ∏X(R);
2. 2. 2. 求 ∏ Y ( S ) \prod{}_Y(S) ∏Y(S);
3. 3. 3. Y X Y_X YX 为 X X X 在 R R R 中的像集(Image Set),它表示 R R R 中属性组上 X X X 值为 x i x_i xi 的各个元组在 Y Y Y 上的分量集合,每个 x i x_i xi 都有一个 Y Y Y 的分量集合;求像集 Y X Y_X YX 的方法:对于每个值 x i ∈ ∏ X ( R ) x_i \in \prod {}_X(R) xi∈∏X(R),求出 ∏ Y ( σ X = x i ( R ) ) \prod {}_Y(\sigma _{X = x_i}(R)) ∏Y(σX=xi(R));
4. 4. 4. R ÷ S R \div S R÷S 运算结果为:像集 Y X Y_X YX 包含了 ∏ Y ( S ) \prod {}_Y(S) ∏Y(S) 的所有 x i x_i xi。
例:设关系 R ( A , B , C ) , S ( B , C , D ) R(A,B,C), S(B,C,D) R(A,B,C),S(B,C,D),如下图所示,求 R ÷ S R\div S R÷S 的结果。

1. 1. 1. 求 ∏ X ( R ) \prod {}_X(R) ∏X(R),易知: ∏ X ( R ) = { a 1 , a 2 , a 3 , a 4 } \prod {}_X(R) = \{a_1, a_2, a_3, a_4\} ∏X(R)={a1,a2,a3,a4},即在关系 R R R 中, A A A 可以取 4 4 4 个值 { a 1 , a 2 , a 3 , a 4 } \{a_1, a_2, a_3, a_4\} {a1,a2,a3,a4};
2. 2. 2. 求 ∏ Y ( S ) \prod {}_Y(S) ∏Y(S),易知: ∏ Y ( S ) = { ( b 1 , c 2 ) , ( b 2 , c 1 ) , ( b 2 , c 3 ) } \prod {}_Y(S) = \{(b_1,c_2),(b_2,c_1), (b_2,c_3)\} ∏Y(S)={(b1,c2),(b2,c1),(b2,c3)};
3. 3. 3. 求 x i x_i xi 或者说 a i , 1 ≤ i ≤ 4 a_i, 1 \le i \le 4 ai,1≤i≤4 在 R R R 中的像集 Y X Y_X YX,对每个 x i ∈ ∏ X ( R ) x_i \in \prod{}_X(R) xi∈∏X(R),求 ∏ Y ( σ X = x i ( R ) ) \prod {}_Y(\sigma _{X = x_i}(R)) ∏Y(σX=xi(R)):
- x 1 = a 1 x_1 = a_1 x1=a1, σ x 1 = a 1 ( R ) \sigma _{x_1=a_1}(R) σx1=a1(R)如下:
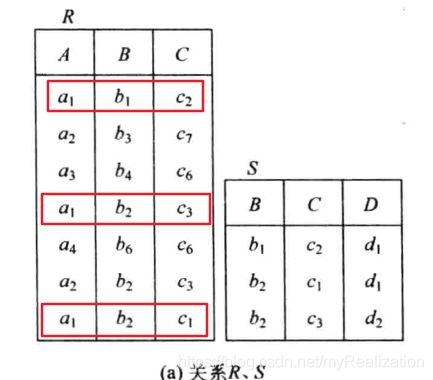
可得在 R R R 中的像集: ∏ Y ( σ x 1 = a 1 ( R ) ) = { { b 1 , c 2 } , { b 2 , c 3 } , { b 2 , c 1 } } \prod {}_Y(\sigma _{x_1=a_1}(R)) = \{\{b_1,c_2\},\{b_2,c_3\},\{b_2,c_1\}\} ∏Y(σx1=a1(R))={{b1,c2},{b2,c3},{b2,c1}} - ∏ Y ( σ x 2 = a 2 ( R ) ) = { { b 3 , c 7 } , { b 2 , c 3 } } \prod {}_Y(\sigma _{x_2=a_2}(R)) = \{\{b_3,c_7\},\{b_2,c_3\}\} ∏Y(σx2=a2(R))={{b3,c7},{b2,c3}}
- ∏ Y ( σ x 3 = a 3 ( R ) ) = { { b 4 , c 6 } } \prod {}_Y(\sigma _{x_3=a_3}(R)) = \{\{b_4,c_6\}\} ∏Y(σx3=a3(R))={{b4,c6}}
- ∏ Y ( σ x 4 = a 4 ( R ) ) = { { b 6 , c 6 } } \prod {}_Y(\sigma _{x_4=a_4}(R)) = \{\{b_6,c_6\}\} ∏Y(σx4=a4(R))={{b6,c6}}
4. 4. 4. 求出像集 B C a i BC_{a_i} BCai 或者说 Y X Y_X YX 中包含了 ∏ Y ( S ) \prod {}_Y(S) ∏Y(S) 的 a i a_i ai,显然,只有 a i a_i ai 在 R R R 中的像集 包含了所有 ∏ Y ( S ) = ∏ B , C ( S ) \prod {}_Y(S) = \prod {}_{B,C}(S) ∏Y(S)=∏B,C(S) ,则 R ÷ S = { a 1 } R\div S = \{a_1\} R÷S={a1}。
关系代数定义了除法运算。但是实际运用中,当关系 R R R 真包含了关系 S S S 时, R ÷ S R\div S R÷S 才有意义。 R R R 能够被 S S S 除尽的充分必要条件是: R R R 中的属性包含 S S S 中的所有属性; R R R 中有一些属性不出现在 S S S 中。
R = ( X , Y ) , S = ( Y ) R = (X,Y), S = (Y) R=(X,Y),S=(Y): 可以这样理解 R ÷ S R \div S R÷S,即 R R R 中包含了 S S S 中全部属性值的那些元组,在 R R R 与 S S S 的属性名集合之差 R − S R - S R−S 即 X X X 上的投影。
5. 实际练习【重点】
设一学生选课关系数据库,见下表,在 3 3 3 个关系中,除学号、年龄、学分、成绩属性的值为整型数外,其余均为字符串型。
s t u d e n t ( s n o , s n a m e , s e x , a g e , d e p t , p l a c e ) c o u r s e ( c n o , c n a m e , c r e d i t , p c n o ) s c ( s n o , c n o , g r a d e ) \begin{aligned} &student(sno,sname,sex,age,dept,place)\\ &course(cno,cname, credit , pcno)\\ &sc(sno,cno,grade) \end{aligned} student(sno,sname,sex,age,dept,place)course(cno,cname,credit,pcno)sc(sno,cno,grade)
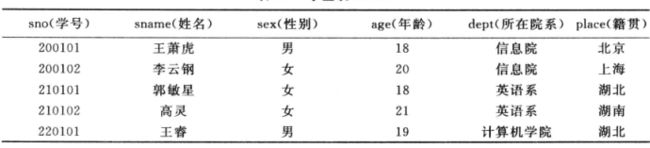
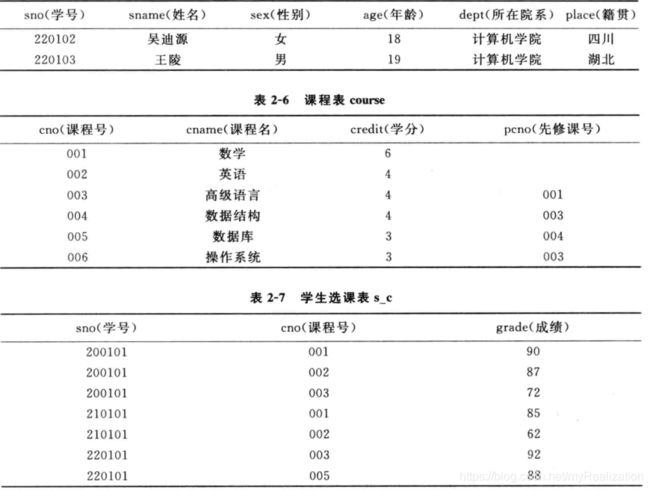
(1)求年龄在 25 25 25 岁以下的女学生:
σ a g e < 25 ∧ s e x = ′ 女 ′ ( S ) \sigma _{age\ <\ 25\ \wedge\ sex='女'}(S) σage < 25 ∧ sex=′女′(S)
(2)求成绩在 85 85 85 分及以上的学生的学号和姓名:
∏ s n o , s n a m e ( σ g r a d e > 85 ( s t u d e n t ⋈ s c ) ) \prod {}_{sno, sname}(\sigma _{grade\ >\ 85}(student \Join sc)) ∏sno,sname(σgrade > 85(student⋈sc))
公共属性是 s n o sno sno。
(3)查询至少选修了一门其 直接先修课为 003 003 003 号课程 的课程的学生姓名。由于涉及到了先修课程号、学生姓名,必然涉及到course表,以及student表,还需要sc表。多表查询,需要自然连接。
∏ s n a m e ( σ p c n o = ′ 00 3 ′ ( s t u d e n t ⋈ s c ⋈ c o u r s e ) ) \prod {}_{sname}(\sigma _{pcno='003'}(student \Join sc \Join course)) ∏sname(σpcno=′003′(student⋈sc⋈course))
可以进一步优化,对于有选择运算的,优先进行选择,以减少笛卡尔积的规模;选择完毕后可以适当增加投影,投影那些后面的自然连接会用到的公共属性,和那些要求的属性。
∏ s n a m e ( ∏ s n o , n a m e ( s t u d e n t ) ⋈ s c ⋈ ∏ c n o ( σ p c n o = ′ 00 3 ′ ( c o u r s e ) ) \prod {}_{sname}(\prod {}_{sno,name}(student) \Join sc \Join \prod {}_{cno}(\sigma _{pcno='003'}(course)) ∏sname(∏sno,name(student)⋈sc⋈∏cno(σpcno=′003′(course))
(4)求选修数据库课程的学生的姓名和成绩。 ∏ s n a m e , g r a d e ( σ c n a m e = ′ 数 据 库 ′ ( s t u d e n t ⋈ s c ⋈ c o u r s e ) ) \prod {}_{sname, grade}(\sigma _{cname='数据库'}(student \Join sc \Join course)) ∏sname,grade(σcname=′数据库′(student⋈sc⋈course))
同样可以进行优化:
∏ s n a m e , g r a d e ( ∏ s n o , s n a m e ( s t u d e n t ) ⋈ s c ⋈ ∏ c n o ( σ c n a m e = ′ 数 据 库 ′ ( c o u r s e ) ) ) \prod {}_{sname, grade}(\prod {}_{sno, sname}(student) \Join sc \Join \prod {}_{cno}(\sigma _{cname='数据库'}(course))) ∏sname,grade(∏sno,sname(student)⋈sc⋈∏cno(σcname=′数据库′(course)))
(5)查询没有选择 005 005 005 号课程的学生的学号。
下面的式子是错误的!
∏ s n o ( σ c n o ≠ ′ 00 5 ′ ( S C ) ) \prod{}_{sno}(\sigma _{cno \ne '005'}(SC)) ∏sno(σcno=′005′(SC))
因为这样是从 选了课程 的学生中进行查找,没有考虑到那些没选课的学生;而且,这样做也会输出那些 选了005号课程但也选了其他课程的学生。因此是大错特错的!
我们应该先找到选了005号课程的学生,然后从所有学生中减去这部分学生。
∏ c n o ( s t u d e n t ) − ∏ c n o ( σ c n o = ′ 00 5 ′ ( S C ) ) \prod {}_{cno}(student) - \prod {}_{cno}(\sigma _{cno = '005'}(SC)) ∏cno(student)−∏cno(σcno=′005′(SC))
(6)查询没有选择 005 005 005 号课程的学生姓名与年龄。
同上:
∏ s n a m e , a g e ( s t u d e n t ) − ∏ s n a m e , a g e ( s t u d e n t ⋈ σ c n o = ′ 00 5 ′ ( S C ) ) \prod {}_{sname,age}(student) - \prod {}_{sname, age}(student \Join \sigma _{cno = '005'}(SC)) ∏sname,age(student)−∏sname,age(student⋈σcno=′005′(SC))
(7)查询选择了全部课程的学生的姓名和学号。
这个怎样做呢?需要用除法,用学生选课表 ÷ \div ÷ 课程表,得到选修了全部课程的学生的学号。然后用得到的学号和学生表进行自然连接。
∏ s n o , c n o ( s c ) ÷ ∏ c n o ( c o u r s e ) ⋈ ∏ s n a m e , s n o ( s t u d e n t ) \prod {}_{sno,cno}(sc) \div \prod {}_{cno}(course) \Join \prod {}_{sname, sno}(student) ∏sno,cno(sc)÷∏cno(course)⋈∏sname,sno(student)
(8)查询至少选择了两门课程的学生学号。
这个题目更麻烦了,需要用差运算,用全部的学生学号-没有选的-选了一门的学生学号。其实简单的想,可以用自己与自己进行笛卡尔积,这里用列号进行区分。
∏ [ 1 ] ( σ [ 1 ] = [ 4 ] ∧ [ 2 ] ≠ [ 5 ] ( s c × s c ) ) \prod {}_{[1]} (\sigma _{[1] = [4]\ \wedge\ [2] \ne [5]} (sc \times sc)) ∏[1](σ[1]=[4] ∧ [2]=[5](sc×sc))
6. 关系代数基本运算总结【重点】
关系代数基本运算是五种:交,差,笛卡尔积,投影,选择:
- 投影: ∏ A 1 , A 2 , . . . , A k ( R ) \prod {}_{A_1,A_2,...,A_k}(R) ∏A1,A2,...,Ak(R) 实现关系属性列的指定;
- 选择: σ F ( R ) \sigma _{F}(R) σF(R) 实现关系行的选择;
- 并: R ∪ S R \cup S R∪S 实现两个关系的合并或者说关系中元组(行)的插入;
- 差: R − S R - S R−S 实现关系中元组(行)的删除;
- 积: R × S R \times S R×S 实现两个关系的无条件全连接。
非基本运算可以用基本运算来表示:
- 交: R ∩ S = R − ( R − S ) R \cap S = R - (R - S) R∩S=R−(R−S);
- 条件连接: R ⋈ i θ j = σ [ i ] θ [ m + j ] ( R × S ) R \Join_{i\ \theta\ j} = \sigma_{[i]\ \theta\ [m + j]} (R \times S) R⋈i θ j=σ[i] θ [m+j](R×S)
- 等值连接: R ⋈ A = B S = σ R . A = S . B ( R × S ) R \Join _{A\ =\ B} S = \sigma_{R.A = S.B}\ (R \times S) R⋈A = BS=σR.A=S.B (R×S)
- 自然连接: R ⋈ S = ∏ A 1 , A 2 , . . . , A k ( σ R . B 1 = S . B 1 ∧ . . . ∧ R . B k = S . B k ( R × S ) ) R \Join S = \prod_{A_1,A_2,...,A_k}\ (\sigma _{R.B_1 = S.B_1\ \wedge\ ...\ \wedge\ R.B_k = S.B_k}\ (R \times S)) R⋈S=∏A1,A2,...,Ak (σR.B1=S.B1 ∧ ... ∧ R.Bk=S.Bk (R×S)),其中 B 1 , B 2 , . . . , B k B_1,B_2,...,B_k B1,B2,...,Bk 为 R R R, S S S 的公共属性,而 A 1 , A 2 , . . . , A k A_1,A_2,...,A_k A1,A2,...,Ak 为从 R R R 与 S S S 的属性集中去掉 S . B 1 , S . B 2 , . . . , S . B k S.B_1,S.B_2,...,S.B_k S.B1,S.B2,...,S.Bk 后剩余的属性;
- 除法:设关系 R ( X , Y ) R(X,Y) R(X,Y), S ( Y , Z ) S(Y,Z) S(Y,Z), X X X、 Y Y Y、 Z Z Z 为属性集, R ÷ S R \div S R÷S 的过程如下:
( 1 ) . (1). (1). T = ∏ X ( R ) T = \prod _X(R) T=∏X(R);
( 2 ) . (2). (2). W = ( T × ∏ Y ( S ) ) − R W = (T \times \prod {}_Y(S)) - R W=(T×∏Y(S))−R:算出 T × ∏ Y ( S ) T\times \prod{}_Y(S) T×∏Y(S) 中不存在于 R R R 中的元组;
( 3 ) . (3). (3). V = ∏ X ( W ) V = \prod{}_X(W) V=∏X(W);
( 4 ) . (4). (4). R ÷ S = T − V R \div S = T - V R÷S=T−V
⇒ R ÷ S = ∏ X ( R ) − ∏ X ( ( ∏ X ( R ) × ∏ Y ( S ) ) − R ) \Rightarrow R \div S = \prod{}_X(R) - \prod{}_X\Big(\big(\prod_X(R) \times \prod_Y(S)\big) - R\Big) ⇒R÷S=∏X(R)−∏X((∏X(R)×∏Y(S))−R)
四、扩充的关系运算
随着数据库的发展和应用情况,关系运算被扩展。
1. 广义投影
设有关系模式 R R R,对其进行广义投影运算 ∏ F 1 , F 2 , . . . , F n ( R ) \prod{}_{F_1,F_2,...,F_n}(R) ∏F1,F2,...,Fn(R),其中 F 1 , . . . , F n F_1,...,F_n F1,...,Fn 涉及到 R R R 中常量和属性的算术表达式。通过这种广义投影运算对投影进行扩充。
例:若将查出的学生关系 s t u d e n t student student 中学号为 000101 000101 000101 学生的年龄加 1 1 1 岁,可以用广义投影运算表示为:
∏ s n o , s n a m e , s e x , a g e = a g e + 1 ( σ s n o = ′ 00010 1 ′ ( s t u d e n t ) \prod {}_{sno, sname,sex,age=age+1}(\sigma_{sno='000101'}(student) ∏sno,sname,sex,age=age+1(σsno=′000101′(student)
2. 赋值
设有相容的关系 R R R 和 S S S ,则通过赋值运算可以对关系 R R R 赋予新的关系 S S S,记为: R ← S R \leftarrow S R←S,其中 S S S 是通过关系代数运算得到的关系。通过赋值,可以把复杂的关系表达式化为若干个简单的表达式进行运算。特别是对于插入、删除和修改操作来说,很方便。
例:在关系 c o u r s e course course 中新增一门新课:(099, 电子商务, 2, 003),可以用赋值操作表示如下:
c o u r s e ← c o u r s e ∪ { 099 , 电 子 商 务 , 2 , 003 } course \leftarrow course \cup \{099,电子商务,2,003\} course←course∪{099,电子商务,2,003}
例:设学号为 200108 的学生因故退学,在关系 student 和 sc中将其相关记录删除,可表示为:
s t u d e n t ← s t u d e n t − ( σ s n o = ′ 20010 8 ′ ( s t u d e n t ) ) s c ← s c − ( σ s n o = ′ 20010 8 ′ ( s c ) ) \begin{aligned} &student \leftarrow student - (\sigma _{sno='200108'}(student))\\ &sc \leftarrow sc - (\sigma _{sno='200108'}(sc))\end{aligned} student←student−(σsno=′200108′(student))sc←sc−(σsno=′200108′(sc))
对关系进行修改时,可以先将要修改的元组删除,再将新元组插入即可。
3. 几种外连接
(1). 外连接
设有关系 R R R 和 S S S,它们的公共属性组成的集合为 Y Y Y,则对 R R R 和 S S S 进行自然连接时,在 R R R 中可能存在某些元组,无法在 Y Y Y 上与 S S S 的任一元组相等;同样对于 S S S 也是如此,可能存在某些元组无法在 Y Y Y 上与 R R R 的任一元组相等。那么当 R ⋈ S R \Join S R⋈S 时,这些元组都会被舍弃。
如果不舍弃这些元组,并且在这些元组新增加的属性上赋空值,这种操作就被称为“外连接”。表示如下……
我在 KaTeX \href{https://katex.org}{\KaTeX} KATEX 找了半天,没看到外连接的符号,算了。
(2). 左外连接
如果只保存 R R R 中原来要舍弃的元组,则称为 R R R 与 S S S 的 “左外连接”。表示为:
R ⟖ S R\ ⟖\ S R ⟖ S
(3). 右外连接
如果只保存 S S S 中原来要舍弃的元组,则称为 R R R 与 S S S 的 “右外连接”。
4. 半连接
设有关系 R R R 和 S S S,则 R R R 和 S S S 的自然连接只在关系 R R R 或 S S S 的属性集上的投影,称为“半连接”。 R R R 和 S S S 的半连接记作 R ⋉ S R \ltimes S R⋉S, S S S 与 R R R 的半连接记作 R ⋊ S R \rtimes S R⋊S 或者 S ⋉ R S \ltimes R S⋉R 。
5. 聚集
关系的聚集是指根据关系中的一组值,经过统计计算得到一个值作为结果。
比较常用的有 max , min , a v g , s u m , c o u n t \max,\min,avg,sum,count max,min,avg,sum,count 等。使用聚集函数时需要在前面写上符号 G G G。
例:对于学生-选课关系数据库的统计:
(1)求男同学的平均年龄: G a v g ( a g e ) ( σ s e x = ′ 男 ′ ( s t u d e n t ) ) G\ avg(age)(\sigma _{sex='男'}(student)) G avg(age)(σsex=′男′(student))
(2)计算年龄不小于 20 20 20 岁的学生人数: G c o u n t ( s n o ) ( σ a g e ≥ 20 ( s t u d e n t ) ) G\ count(sno)(\sigma _{age\ge 20}(student)) G count(sno)(σage≥20(student))
(3)计算选修数据库课程的平均分数: G a v g ( g r a d e ) ( ∏ c n o ( σ c n a m e = ′ 数 据 库 ′ ( c o u r s e ) ) ⋈ s c ) G\ avg(grade)(\prod _{cno}(\sigma _{cname='数据库'}(course)) \Join sc) G avg(grade)(∏cno(σcname=′数据库′(course))⋈sc)
6. 外部并
设有关系 R R R 和 S S S, R R R 和 S S S 的外部并得到一个新关系,其属性由 R R R 和 S S S 中的所有属性组成,公共属性仅取一次,其元组由属于 R R R 或属于 S S S 的元组组成,且元组在新增加的属性上填上空值。
7. 重命名
- ρ x ( E ) ρ_x(E) ρx(E):其含义为 给一个关系表达式赋予名字。它返回表达式 E E E 的结果,并把名字 x x x 赋给 E E E。
- ρ x ( A 1 , A 2 , … … , A n ) ( E ) ρ_x(A_1,A_2,……,A_n)(E) ρx(A1,A2,……,An)(E):其含义为返回表达式 E E E 的结果,并把名字 x x x 赋给 E E E,同时将各属性更名为 A 1 , A 2 , … … , A n A_1,A_2,……,A_n A1,A2,……,An 。
实际上,关系可以被看做一个最小的关系代数式,可以将重命名运算施加到 关系 或 属性 上,得到具有不同名字的 同一关系 或 不同属性名的 同一关系 。这对同一关系多次参与同一运算时很有用。
例:设关系 R ( 姓 名 , 课 程 , 成 绩 ) R(姓名,课程,成绩) R(姓名,课程,成绩),求数学成绩比王红同学高的学生。
解:因为在同一关系上难以进行比较,采用重命名运算:
∏ S . 姓 名 ( ( σ 课 程 = ′ 数 学 ′ ∧ 姓 名 = ′ 王 红 ′ ( R ) ) ⋈ R . 成 绩 < S . 成 绩 ( σ 课 程 = ′ 数 学 ′ ρ S ( R ) ) ) \prod {}_{S.姓名}((\sigma _{课程='数学' \wedge 姓名='王红'}(R)) \Join_{R.成绩 \lt S.成绩} (\sigma _{课程='数学'}\ \rho_S(R))) ∏S.姓名((σ课程=′数学′∧姓名=′王红′(R))⋈R.成绩<S.成绩(σ课程=′数学′ ρS(R)))
8. 扩充运算示例【重点】
需要注意的是,无论是外连接,还是半连接,都是基于自然连接之上的。这些连接的例子,有 R R R 和 S S S 关系如下:
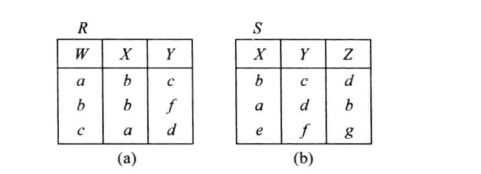
自然连接 R ⋈ S R \Join S R⋈S 是建立在公共属性 X , Y X,Y X,Y 上的等值连接,连接后需要抛弃 S S S 中多余的公共属性 S . X , S . Y S.X,S.Y S.X,S.Y,保留 R R R 中没有的 S S S 的属性 S . Z S.Z S.Z,保留 S S S 中没有的 R R R 的属性 R . W R.W R.W。

可以看出,画了紫色下划线的这两个元组,无法在公共属性上与另一个关系中的任一元组相等,因此在自然连接中会被舍弃。

如果保留左边 R R R 的那些要被舍弃的元组,并在新的属性 Z Z Z 上赋空值的话,这就是左外连接:
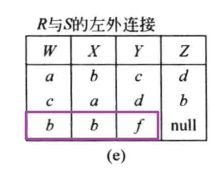
如果保留右边 S S S 的那些要被舍弃的元组,并在新的属性 R . W R.W R.W 上赋空值的话,这就是右外连接:
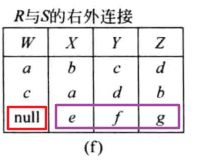
如果同时保留两边要舍弃的元组,并在各自新的属性上赋空值,这就是外连接:

注意,这些都是要被舍弃的元组!它们不会发生自然连接!
半连接基于自然连接,但和外连接不同,半连接仅仅保留一边的属性。
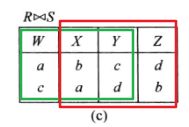
对于 R ⋈ S R\Join S R⋈S,保留 R R R 的属性, R R R 和 S S S 的半连接记作 R ⋉ S R \ltimes S R⋉S, S S S 与 R R R 的半连接记作 S ⋉ R S \ltimes R S⋉R:
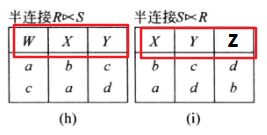
另外,需要清楚的是外部并,并运算是集合运算,基于同类关系;外部并可以对不同类的关系进行运算,其结果的属性列为 R R R 和 S S S 属性列的并集,其中公共属性只取一次;结果的行为 R R R 和 S S S 记录的并集,只不过它们各自对新增的属性列填上空值:

五、实际练习
1、设有下图所示的5个关系表 R R R、 S S S、 T T T、 U U U和 V V V,请写出下列各种运算结果。

(1) R ∪ S R∪S R∪S
解:

(2) R ∩ S R∩S R∩S
解:

(3) R × S R×S R×S
解:

(4) U ÷ V U÷V U÷V
解:可得,公共属性为 Z , W Z,W Z,W:
a . a. a. ∏ X , Y ( U ) = { ( a , b ) , ( c , a ) } \prod {}_{X,Y}(U) = \{(a,b),(c,a)\} ∏X,Y(U)={(a,b),(c,a)};
b . b. b. ∏ Z , W ( V ) = { ( e , f ) , ( c , d ) } \prod {}_{Z,W}(V) = \{(e,f),(c,d)\} ∏Z,W(V)={(e,f),(c,d)};
c . c. c. 求像集如下:
- 对于 ( a , b ) (a,b) (a,b),有 ∏ Z , W ( σ X = a ∧ Y = b ( U ) ) = { ( c , d ) , ( e , f ) } \prod {}_{Z,W}\Big(\sigma _{X=a\ \wedge\ Y = b}(U)\Big) = \{(c,d),(e,f)\} ∏Z,W(σX=a ∧ Y=b(U))={(c,d),(e,f)};
- 对于 ( c , a ) (c,a) (c,a),有 ∏ Z , W ( σ X = c ∧ Y = a ( U ) ) = { ( c , d ) } \prod {}_{Z,W}\Big(\sigma _{X=c\ \wedge\ Y = a}(U)\Big) = \{(c,d)\} ∏Z,W(σX=c ∧ Y=a(U))={(c,d)}.
d . d. d. 可以发现,包含了 ∏ Z , W ( V ) ∏{}_{Z,W}(V) ∏Z,W(V) 的只有 ( a , b ) (a,b) (a,b),所以 U ÷ V = { ( a , b ) } U \div V = \{(a,b)\} U÷V={(a,b)}.
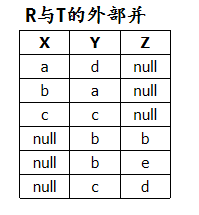
(5) R R R 与 T T T 的外部并
解:
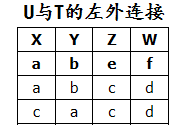
(6) U U U 与 T T T 的外连接、左外连接及右外连接
解:


(7) T ⋈ S T ⋈ S T⋈S

2、已知学生表 S S S、仼课表 C C C 和选课表 S C SC SC 如下所示,试用关系代数表示下列查询。
- S(sno,sname,sex,age)
- C(cno,cname,teacher)
- SC(sno,cno,grade)
(1)查询"张景林"老师所授课程号和课程名。
答: ∏ c n o , c n a m e ( σ t e a c h e r = ′ 张 景 林 ′ ( C ) ) \prod {}_{cno, cname}(\sigma _{teacher='张景林'}(C)) ∏cno,cname(σteacher=′张景林′(C))
(2)查询选修课程名为"C语言"或者"数据库"的学生号。
答: ∏ s n o ( ∏ c n o ( σ c n a m e = ′ C 语 言 ′ ∨ c n a m e = ′ 数 据 库 ′ ( C ) ) ⋈ S C ) \prod {}_{sno}\bigg(\prod {}_{cno}\Big(\sigma _{cname='C语言'\ \vee\ cname = '数据库'}(C)\Big) \Join SC\bigg) ∏sno(∏cno(σcname=′C语言′ ∨ cname=′数据库′(C))⋈SC)
(3)查询"高晓灵"同学所选俢课程的课程号及课程名。
答: ∏ c n o , c n a m e ( ∏ s n o ( σ s n a m e = ′ 高 晓 灵 ′ ( S ) ) ⋈ S C ⋈ C ) \prod {}_{cno, cname}\bigg(\prod {}_{sno}\Big(\sigma _{sname='高晓灵'}(S)\Big) \Join SC \Join C\bigg) ∏cno,cname(∏sno(σsname=′高晓灵′(S))⋈SC⋈C)
(4)查询至少选俢两门课程的学生学号。
答: ∏ [ 1 ] ( σ [ 1 ] = [ 4 ] ∧ [ 2 ] ≠ [ 5 ] ( S C × S C ) ) \prod {}_{[1]} (\sigma _{[1] = [4]\ \wedge\ [2] \ne [5]} (SC \times SC)) ∏[1](σ[1]=[4] ∧ [2]=[5](SC×SC))
(5)查询全部学生都选修的课程的课程号和课程名。
答: ∏ s n o , c n o ( S C ) ÷ ∏ s n o ( S ) ⋈ ∏ c n o , c n a m e ( C ) \prod {}_{sno,cno}(SC) \div \prod {}_{sno}(S) \Join \prod {}_{cno, cname}(C) ∏sno,cno(SC)÷∏sno(S)⋈∏cno,cname(C)
(6)查询至少选修"张景林"老师所授全部课程的学生姓名。
答: ∏ s n a m e ( ∏ s n o , s n a m e ( S ) ⋈ ( ∏ s n o , c n o ( S C ) ÷ ∏ c n o ( σ t e a c h e r = ′ 张 景 林 ′ ( C ) ) ) ) \prod {}_{sname}\Bigg(\prod {}_{sno,sname}(S) \Join \bigg( \prod {}_{sno,cno}(SC)\div \prod {}_{cno}(\sigma _{teacher='张景林'}(C))\bigg) \Bigg) ∏sname(∏sno,sname(S)⋈(∏sno,cno(SC)÷∏cno(σteacher=′张景林′(C))))