信息安全技术概述
一. 密码技术基础
密码技术是为了维护数据安全,其目标主要包括 机密性、真实性、完整性、不可否认性、可用性、可控性密码学(Cryptology)主要,包括:
密码编码学:研究如何进行数据加密和解密(保证数据的机密性),以及防止和发现数据的伪造、篡改(保证数据的真实性、完整性、不可否认性)
密码分析学:分析发现密码算法的弱点、缺陷,破解密码算法或者破译密码数据
加解密流程
二. 密码算法
概述
设:M是可能明文的集合(明文空间)
C是可能密文的集合(密文空间)
K是一切可能密钥构成的集合(密钥空间)
E为加密算法,它对密钥空间的任一密钥k都能进行加密运算,即Ek: M->C
D为解密算法,它对密钥空间的任一密钥都能进行解密运算,即Dk: C->M
则密码算法具有如下性质:
(2)密码破译者获得密文c=Ek(x)后无法在有效的时间内破解出密钥k和/或明文x
数论基础
定义1. 设n为大于1的正整数,a为任一整数,a可表示为a=kn +r,0≤ r
例,若 –n 定义 3. n为大于1的正整数,a、b为整数,则a+b mod n,a-b mod n ,a*b mod n,ab mod n分别称为整数的模n加法、减法、乘法和乘方(幂) 注意:没有除,但有逆! 设n为大于1的正整数,a、b为任意整数,mod算子的运算优先级最低,则 5) a + (b mod n) mod n = a+b mod n 6) a*(b mod n) mod n = a*b mod n 对于同一个模n,只要保存最外层的mod n算子,给加、减、乘、乘方运算中的数加上或去掉mod n算子,不影响结果 定义 4. 设n为大于1的正整数,a、b为任意整数,若a+b mod n= 0,则b称为a的模n加法逆,记为-a 注意:a的模n乘法逆不止一个,它们相差kn 定义 6. 设p是大于1的正整数,若p只能分解为1和自己的乘积,则p称为素数 推理 1. 设n是素数,则任何非kn整数a存在模n乘法逆a-1 加密和解密使用同一个密钥 对称密钥数字加密分为流加密和分组加密 用一个伪随机密钥流(pseudorandom keystream)与数据流 (按位或按字节)进行异或(XOR)操作 自同步流加密(self-synchronous stream cipher)或异步流加密(asynchronous stream cipher) 随着计算技术的发展,DES越来越不能满足安全要求,特别是其密钥长度56位太短,使得可以通过蛮力攻击(brutal force attack)破解密码,通过应用三重DES算法、使用超过56位的密钥提高DES的安全,到目前为止,AES是安全的,尚未有有效的攻击 DES-EDE2,加密时依次进行加密-解密-加密变换,其中第一次、第三次变换的密钥相同,解密是逆过程,密钥长度112位 对称密码特点 算法实现简单 密钥分发难 Public Key Cryptography 涉及一对密钥,一个可公开,称为公钥(Public Key),一个由拥有者安全保存,称为私钥(Private Key),公钥用于数据加密或签名验证,私钥用于数据解密或数字签名,也称非对称密钥密码体系,Asymmetric Key Cryptography 单向门限函数:单向陷门函数f(x)满足如下三个条件 素数的原根(Primitive Root):素数p的一个原根是一个正整数g^(i)mod p(i=1,2,3...p-1)不同,且包含了1到p-1的所有整数; 若g是素数p的一个原根,则: (1)g,g mod p、g2 mod p,…,gp-1 mod p生成了{1,2,…,p-1}; (2)对应任意整数1 ≤ b ≤ p-1,存在一个唯一的1 ≤ i ≤ p-1,使得b=gi mod p 定理. 对于任意素数p存在原根(一个或多个) 离散对数:若n为大于1的正整数,m为整数,若b = m^i mod n,则b称为m的模n下的 i次幂(i次方),i称为b的以m为基数的模n下的离散对数 (y, p, g)是Bob的私钥,(Z, p, g)是Bob的公钥,(x, p, g)是Alice的私钥,(W, p, g)是Alice的公钥,通信双方首先将各自的公钥传输给对方,然后进行运算得到K。 详细介绍见https://blog.csdn.net/qq_30866297/article/details/51175305 下面给给算法应用代码,想要的直接私我就行了:https://download.csdn.net/download/qq_20587295/10359833 1)Fermat’s little theorem 如果a和n是互素的正整数,则a^φ(n) mod n = 1,φ(n)是欧拉函数 若n是素数,则φ(n)=n-1, 若n=pq,p、q是互异的素数,则φ(n)=(p-1)(q-1) 算法描述: 1)选择两个互异的大素数p和q,计算n=pq,计算φ(n)=(p-1)(q-1) 解密运算:m=c^d mod n (使用私钥) 算法有效性: 解密运算:m=c^e mod n (使用公钥e) ElGamal加密算法,基于循环群(Cyclic group),可用于任何循环群,包括椭圆曲线上的点构成的循环群(ECC密码算法) 例如:若Z*p={1,2,…,p-1},p为素数,任意a、b ∈ Z*p,a*b定义为ab mod p,则Z*p就是一个乘法循环群,它的一个原根g可生成Z*p的所有元素,即Z*p={g, g2, …, gp-1} (mod p?) 设g是Z*p的一个大原根(Primitive root),即gi mod p,i=1,…,p-1,生成Z*p的所有元素 Bob将(c1, c2)=(gy mod p, m*s mod p)发送给Alice 数据解密 = (m mod p)*(s*s-1 mod p) mod p = m 算法实现复杂 多数算法适合分组加密 发送方 对密码系统的常用攻击方法 唯密攻击(Ciphertext only attack) PKI安全体系 PKI(Public Key Infrastructure),公钥基础设施,一个基于公开密钥密码算法、技术的安全技术体系和一个安全信任体系 数字证书由CA证书认证机构通过CA证书认证系统签发 单证书体系,即一个最终用户证书及私钥既用于数据加密和解密,又用于数字签名和签名验证 双证书体系,即一个最终用户有两个证书,一个用于数据加密,另一个用于数字签名 应用:安全电子邮件的应用 身份鉴别包括身份标识(Identification)和身份鉴别(Authentication)两部分 常用登录鉴别技术 会话(Session)是两个端点之间的应用层的逻辑连接 HTTP Cookie Cookie是Web系统返回、并在客户端浏览器设置的信息,浏览器每次访问对应的Web系统时会自动提交此信息;Cookie内容由Web系统决定,Cookie分为临时(或会话)Cookie和永久Cookie,Cookie中可放置会话连接维护信息,如会话ID 用户浏览器提交到Web系统的HTTP请求的URL中包含会话连接信息 隐藏表单数据(Hidden Form Data) 用户通过浏览器提交到Web系统的请求中将包含隐藏表单中的信息 会话对象(Session Object) 可以由Web服务器、动态页面运行环境 (Web容器)、应用程序维护 基于Cookie的单点登录 利用Cookie可设置作用路径(Path)和域(Domain)的特性,在多个系统间共享Cookie 设置Path=/abc/ 若多个系统是同一个域的子域,则可将Cookie的作用域设置为共同的域,从而多个系统可共享Cookie 当一个用户在一个系统完成登录鉴别后,系统将标志用户已完成登录的安全令牌设置为共享Cookie,当用户访问其他系统时,其他系统通过共享Cookie知道用户已完成登录鉴别及用户的身份信息 Kerberos协议
表示为 a ≡ b (mod n)
a、b模n同余当且仅当n整除a-b,或者说(a-b)modn=0
1) a + b mod n = (a mod n) + (b mod n) mod n
2) a – b mod n = (a mod n) + (–b mod n) mod n = (a mod n) – (b mod n) mod n
3) ab mod n = (a mod n)*(b mod n) mod n
4) a mod n = a + kn mod n = a – kn mod n
7) (a mod n)p mod n = ap mod n
结论:
注意:a的模n加法逆不止一个,它们相差kn
定义 5. 设n为大于1的正整数,a、b为任意整数,若 ab mod n= 1,则b称为a的模n乘法逆,记为a-1,即a*a-1 mod n=1
定义 7. 设a和b是大于1的正整数, 且a和b的最大公因子是1,即 gcd(a,b)=1,则称为a和b互素
定理 1. 设a和n是大于1的正整数,且a和n互素,则a存在模n乘法逆a-1对称秘钥密码
(1)流密码
接收方,用同一个伪随机密钥流对密文数据进行异或(XOR)操作(解密)
根据伪随机密钥流生成方式的不同分为
同步流加密(synchronous stream cipher)
(2)分组密码
DES算法
3DES的四种模式
DES-EEE3,使用三个不同的DES密钥顺序进行三次加密变换,解密是逆过程,密钥长度168位
DES-EDE3,加密时使用三个不同的DES密钥依次进行加密-解密-加密变换,解密是逆过程,密钥长度168位
DES-EEE2,进行三次加密变换,其中第一次、第三次变换的密钥相同,解密是逆过程,密钥长度112位
速度快
密钥短公钥密码体系
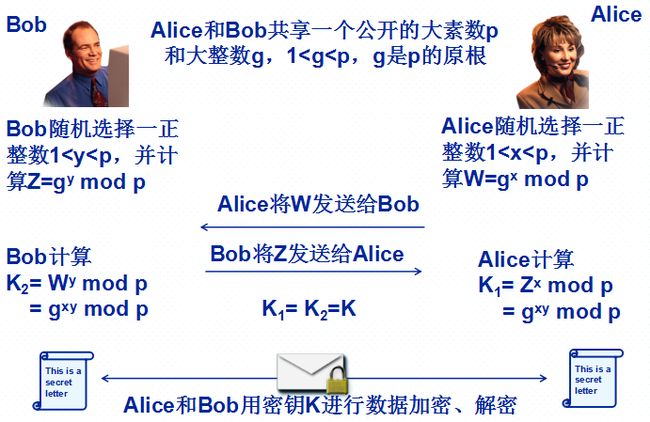
Diffie-Hellman算法
离散对数难题
对于函数y=m^x mod n,已知m、n、x计算y是容易的,反之,已知m、n、y计算x是困难的ECC算法
RSA算法
数学基础:数论中的欧拉(Euler)定理或费马小定理(Fermat’s little theorem)和大整数的因子分解难题
若p为素数,则对于任意整数a,有
a^p mod p = a mod p
若进一步地,如p不能除a(即a≠ kp),则有
a^(p-1) mod p = 1
2)欧拉定理
4)已知两个互异的大素数p、q,计算n=pq是容易的;反之,若已知n是两个素数p、q的乘积,分解出p、q却是很困难的
2)选择整数 1
e*d mod φ(n) =1,其中, 1
以上(1)到(4)由私钥拥有者完成
5)对于明文m, 0≤m
d是e的模φ(n)乘法逆元,e*d mod φ(n)=1,故存在一个正整数k使得e*d=kφ(n)+1
c^d mod n = (m^e mod n)d mod n = m^(ed) mod n
= m^(kφ(n)+1 )mod n = m
6)将使用e、d的顺序换一下,结果同样正确(用于数字签名)
加密运算:c=m^d mod n (使用私钥d)ElGamal加密算法
群:一个定义了乘法(或加法)包含”1”(或”0”)元素的集合,集合中的任何一个元素都存在乘法(或加法)逆
循环群,集合中的所有元素可由一个元素g按乘法幂g^i生成(或加法倍乘i*g生成)椭圆曲线上的点构成了循环群
密钥生成
Alice 随机生成一个整数x,1
Alice保存x作为其私钥,将 (h, g, p)作为公钥发布
数据加密
Bob随机生成一个整数y,1
Bob计算(加密) c2 = m*s mod p
Alice计算共享秘密 (c1)x mod p =gxy mod p=s (D-H密钥)
Alice计算得到s模p乘法逆s-1
Alice计算(解密) c2*s-1 mod p = (m*s*s-1 mod p)
相对于对称密钥密码算法,速度较慢
有的算法密钥长度长(如RSA, EIGamal算法)
密钥分发容易
通常采用非对称密钥密码算法和对称密钥密码算法相结合的方案:随机对称密钥加密数据,非对称密钥加密随机对称密钥
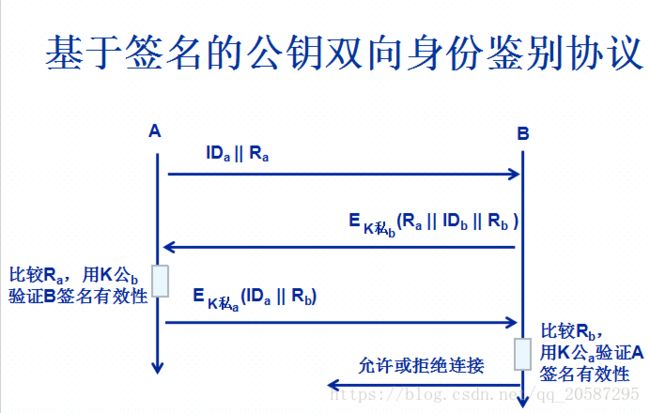
有些算法既可用于数据加密,又可用于抗抵赖数字签名RSA数字签名
接收方
已知明文攻击(Known plaintext attack)
选择明文攻击(Chosen plaintext attack)
PKI的核心是CA(Certification Authority,认证中心),由CA签发和发布证明最终实体(End-Entity)拥有公钥的数字证书
数字证书(Digital Certificate)是一种特别的电子文件,其目的是将公钥与用户或实体绑定,并限定公钥的用途,其格式是X509身份鉴别
身份标识,即确定你是谁并颁发一个身份凭证,如身份证、用户名/口令、数字证书
身份鉴别,即根据你提交的身份凭证并通过特定信息、物件、特征,验证确定你就是你声称的人,而不是假冒者
用户名/口令
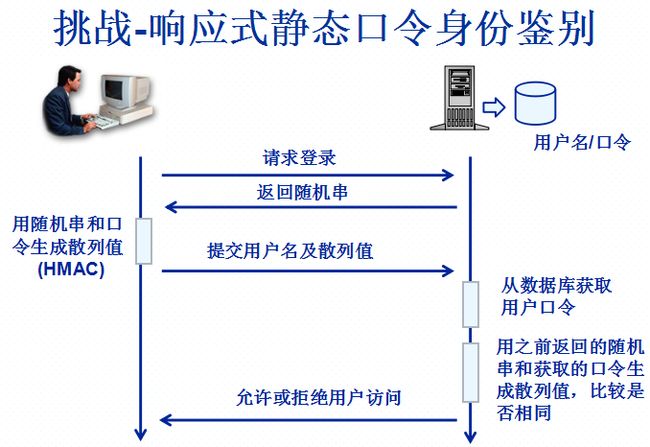
静态口令
动态口令
生物特征
服务器交互中的身份鉴别技术
安全的服务器登录技术
Web系统的会话
应用系统通过会话机制来识别客户端的用户(逻辑连接),以及维护用户的信息(如用户是否已完成身份鉴别、用户名是什么、有哪些权限等),Web系统的传输协议HTTP本身是无连接的传输协议,既可以使用TCP也可以使用UDP传输, 同一个会话可以采用不同的TCP连接。HTTP不维护Web客户端与Web服务器之间的会话连接,Web系统需要采用其他机制维护客户端与服务端之间的会话,包括会话连接和用户信息
Web系统返回到浏览器的Web页面中的URL(如超链接)中保存有会话连接信息
Web系统返回到浏览器的Web页面中包含隐藏表单(Form),隐藏表单中包含有会话连接信息
Web系统服务端的数据对象
会话对象由会话标识符(Session ID)标识SSO技术
Path=/mail/
Domain=.sina.com.cn
若多个系统具有共同的路径,则可将Cookie的作用路径设置为共同路径,从而多个系统可共享Cookie
www.example.com/abc/admin/
www.example.com/abc/user/
mail.sina.com.cn
blog.sina.com.cn
Domain=.sina.com.cn基于SSO 协议的单点登录
HTTP Negotiate
SAML(Security Assertion Markup Language)
WS-Federation
WS-Federation Passive Requestor Profile