改进张益唐证明,陶哲轩「他的证明比我还强」
原标题:改进张益唐证明,陶哲轩「他的证明比我还强」,这个天才青年还解决了困扰数学界近 80 年的「简单问题」
鱼羊 萧箫 发自凹非寺
量子位报道公众号 QbitAI
传奇数学家张益唐之后,又有一位跟「孪生素数猜想」有关的数学家,摘下了「数论界最高奖」柯尔奖。
26 岁时,他不仅将猜想中素数间隔的上限由 7000 万降到了 600,大幅优化了张益唐的结果,还被陶哲轩亲口称赞:说实话,他的描述方式实际上比我的更干净……事实证明他的说法还略强。
而就在拿下柯尔奖前不久,这位来自牛津大学的青年数学家James Maynard,又和另一位数学家合作,攻下了一个困扰数学家们将近 80 年的难题——
Duffin-Schaeffer 猜想。
这一用有理数逼近无理数的问题,对于丢番图逼近领域的数学家来说,几乎可以说是最基础、最关键的问题之一。
改进张益唐最佳结果
张益唐一举成名,是因为「孪生素数猜想」。
猜想听起来很简单:证明存在无穷多对间隔为「有限」的质数。
只不过,张益唐证明的间隔为 7000 万,而这位数学家,James Maynard,直接将这个间隔缩小到了 600。
基于 James Maynard 的方法,有团队再次将间隔缩小到了 246,并推测间隔还能更小,可以说,他的方法带来了里程碑上的突破。
差不多是在同时,大洋彼岸的陶哲轩也在同一问题上,得出了基本相同的结果。
据 QuantaMagazine 报道,当时,James Maynard 还是名博士后,并没有多大名气。
但在读过 James Maynard 的证明方法后,陶哲轩认为,其证明方法比自己的更简洁。
出于惜才之心,陶哲轩主动放弃了与他一同发表这项研究的机会,以免自己的名气掩盖了年轻数学家的成就。
而事实证明,James Maynard 确实潜力无穷。
△ James Maynard 在思考质数问题
在他获得博士学位后的数年中,他在数论领域的长足进步,使得他声名鹊起。2017 年,时年 30 岁的他受聘成为牛津大学数学学院教授。
作为一名数论学家,他最新的「战绩」,是解决了一个曾困扰数学家们近 80 年的难题:Duffin-Schaeffer 猜想。
搞定 Duffin-Schaeffer 猜想
Duffin-Shaeffer 猜想是度量丢番图逼近中的一个重要猜想,由物理学家 Richard Duffin 和数学家 Albert Schaeffer 在 1941 年提出。
所谓丢番图逼近,是数论的一个分支,研究的是用有理数逼近实数。
我们知道,大部分的实数都是π、√2 这样的无理数,它们是无法用分数来表示的。
Duffin 和 Schaeffer 提出的猜想是这样的:
假设 f:N→R≥0是具有正值的实值函数,只有当级数
是发散的(q>0,φ(q)为欧拉函数,表示比q小且与q互质的正整数的个数),对于无理数 α 而言,就存在无穷多个有理数,满足不等式 α-(p/q) < f (q)/q。
也就是说,在寻找近似值的时候,先不考虑分子,而是从自然数中选出无穷多个数字作为分母。
然后,基于分母序列和指定的近似精度范围,来选择分子。
结果就是,如果无穷级数发散,就意味着已经近似了所有无理数;否则,就没有实现对任何无理数的近似。
这一猜想在有理近似中,普遍被数学家们认为是正确的标准,但如何证明它,却成为了困扰数学家们将近 80 年的问题。
而 James Maynard 和蒙特利尔大学的 Dimitris Koukoulopoulos 合作,用 44 页纸的论文一举证明了这一猜想。
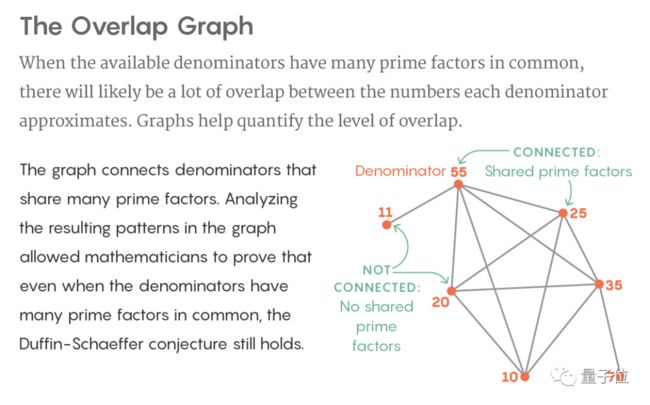
在他们的证明中,他们用分母创建了一个图:把分母绘制成图上的点,如果两个点有许多共同的质因数,就用线将两点连接起来。
这样一来,图的结构就编码了每个分母所近似的无理数之间的重叠。原本这种重合度是难以直接测定的。
利用这种方法,他们证明了 Duffin-Schaeffer 猜想确实是正确的。
△图源:QuantaMagazine
QuantaMagazine 对此评价道:
这是数学领域最罕见的壮举之一:Koukoulopoulos 和 Maynard 给出了自己研究的领域中基本问题的最终答案。
Duffin-Schaeffer 猜想,这个世纪以来曾多次有数学家挑战,但都以失败告终的问题,最终能被 James Maynard 所解决,看似出乎意料,实则在情理之中。
毕竟,James Maynard 一直很「叛逆」。
锋芒毕露:叛逆的天才
出生在人文气息浓厚的家庭氛围里,James Maynard 唯独对数学情有独钟,学习中也表现得有点「离经叛道」:
据 QuantaMagazine 报道,一次物理考试中,规定如果不给计算过程,答案即使全对,也只有满分的⅓。
为了抗议,James Maynard 所有的题目都只写了答案,全对,但只拿了不到一半的分数。
不仅学习上如此,学术研究上也是如此。
在面对那些让人感兴趣的问题时,James Maynard 的第一反应都是:为什么不试试?
即使那些问题在学术界看来难以解决,在他这里也不是绊脚的理由。
当初在证明「孪生素数猜想」时,James Maynard 就曾得到过导师的警告:「我确信你无法解决这个问题,所以你没必要全力以赴。」
但这恰恰与 James Maynard「一不做,二不休」的人生信条相反。
面对导师的告诫,这位年轻叛逆的数学家只是耸耸肩,然后全身心地投入到数学研究中,最终完美地证明了这个问题,而这次的 Duffin-Schaeffer 猜想证明亦是如此。
除此之外,他还解决过几个质数相关的「简单」问题,听起来简单,论证却无比麻烦,感兴趣的同学们,不妨来试试:
1、不含数字「7」的质数有无限个。
2、不含「0-9」中任何一个给定数字的质数有无限个。
这个本硕于剑桥完成、并在牛津获得博士学位的天才数学家,年仅 33 岁就已获得过拉马努金奖(2014)、高级怀特海奖(2015)、欧洲数学学会奖(2016)等各大奖项,今年又获得了号称「数论界最高奖」的柯尔数论奖。
未来这位数论学家还会继续解决哪些问题,值得我们期待。
参考链接:
https://www.quantamagazine.org/james-maynard-solves-the-hardest-easy-math-problems-20200701/
https://en.wikipedia.org/wiki/JamesMaynard (mathematician)
https://www.scientificamerican.com/article/new-proof-solves-80-year-old-irrational-number-problem/