机器学习基础随笔（6）Deep Learning

Deep Learning

参考资料：台湾大学李宏毅机器学习课程和PPT

Deep learning跟machine learning一样，也是“大象放进冰箱”的三个步骤：

在Deep learning的step1里define的那个function，就是neural network神经网络
我个人的理解：深度学习就是多层神经网络，有着多层隐藏层，所以显得有“深度”

Neural Network

concept

把多个Logistic Regression前后连接在一起，然后把一个Logistic Regression称之为neuron（神经元），整个称之为neural network

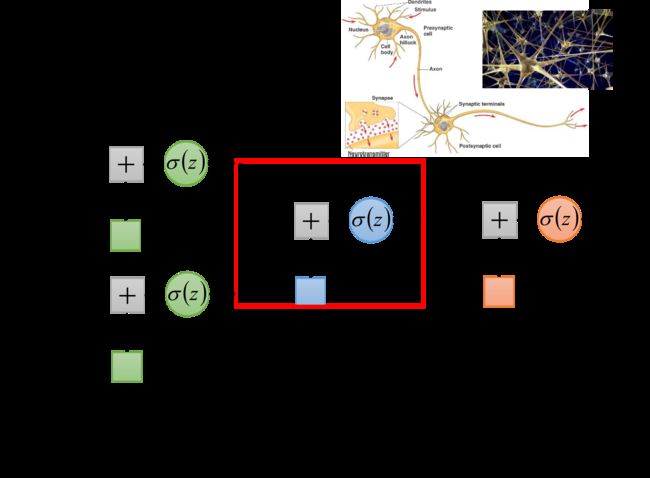
我们可以用不同的方法连接这些neuron，就可以得到不同的structure，neural network里的每一个Logistic Regression都有自己的weight和bias，这些weight和bias集合起来，就是这个network的parameter，我们用$\theta$来描述

Fully Connect Feedforward Network

那该怎么把它们连接起来呢？这是需要你手动去设计的，最常见的连接方式叫做Fully Connect Feedforward Network(全连接前馈网络)

如果一个neural network的参数weight和bias已知的话，它就是一个function，它的input是一个vector，output是另一个vector，这个vector里面放的是样本点的feature，vector的dimension就是feature的个数

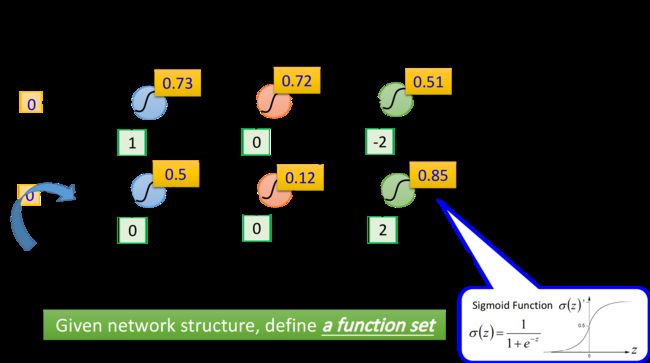
如果今天我们还不知道参数，只是定出了这个network的structure，只是决定好这些neuron该怎么连接在一起，这样的一个network structure其实是define了一个function set(model)，我们给这个network设不同的参数，它就变成了不同的function，把这些可能的function集合起来，我们就得到了一个function set

只不过我们用neural network决定function set的时候，这个function set是比较大的，它包含了很多原来你做Logistic Regression、做linear Regression所没有办法包含的function

下图中，每一排表示一个layer，每个layer里面的每一个球都代表一个neuron

• layer和layer之间neuron是两两互相连接的，layer 1的neuron output会连接给layer 2的每一个neuron作为input
• 对整个neural network来说，它需要一个input，这个input就是一个feature的vector，而对layer 1的每一个neuron来说，它的input就是input layer的每一个dimension
• 最后那个layer L，由于它后面没有接其它东西了，所以它的output就是整个network的output
• 这里每一个layer都是有名字的
  • input的地方，叫做input layer，输入层(严格来说input layer其实不是一个layer，它跟其他layer不一样，不是由neuron所组成的)
  • output的地方，叫做output layer，输出层
  • 其余的地方，叫做hidden layer，隐藏层
• 每一个neuron里面的sigmoid function，在Deep Learning中被称为activation function(激励函数)，事实上它不见得一定是sigmoid function，还可以是其他function(sigmoid function是从Logistic Regression迁移过来的，现在已经较少在Deep learning里使用了)
• 有很多层layers的neural network，被称为DNN(Deep Neural Network)

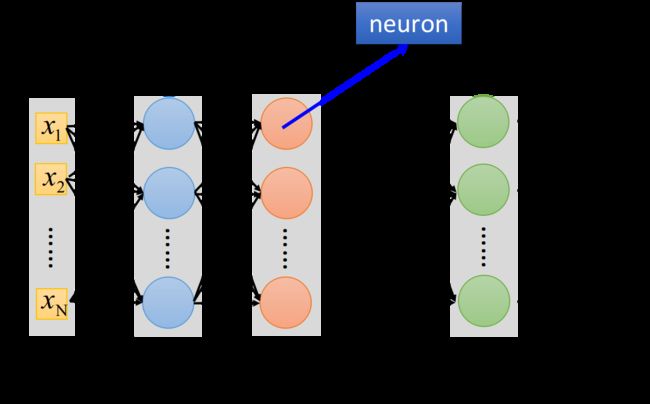
因为layer和layer之间，所有的neuron都是两两连接，所以它叫Fully connected的network；因为现在传递的方向是从layer 1->2->3，由后往前传，所以它叫做Feedforward network

那所谓的deep，是什么意思呢？有很多层hidden layer，就叫做deep，具体的层数并没有规定，现在只要是neural network base的方法，都被称为Deep Learning，下图是一些model使用的hidden layers层数举例

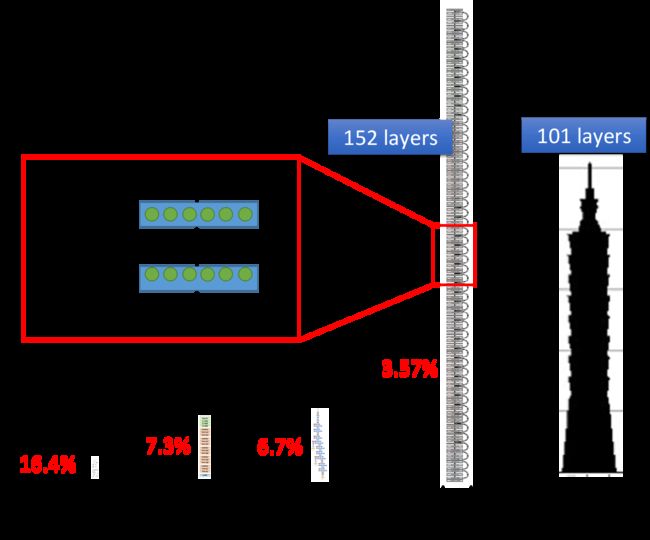
你会发现使用了152个hidden layers的Residual Net，它识别图像的准确率比人类还要高当然它不是使用一般的Fully Connected Feedforward Network，它需要设计特殊的special structure才能训练这么深的network

Matrix Operation

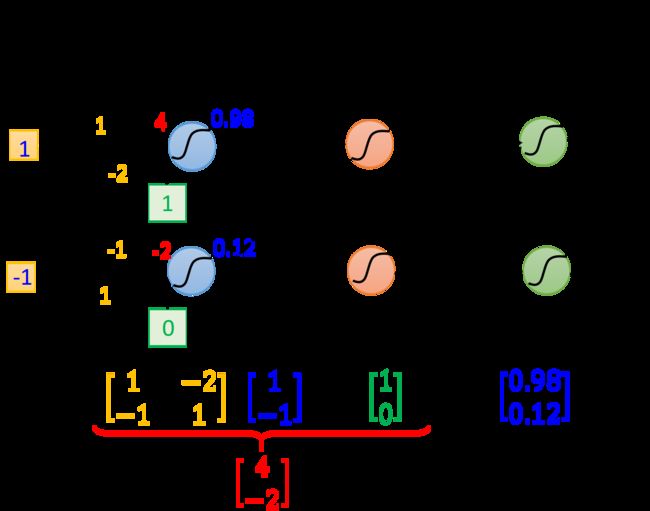
network的运作过程，我们通常会用Matrix Operation来表示，以下图为例，假设第一层hidden layers的两个neuron，它们的weight分别是$w_1=1,w_2=-2,w_1^{\prime }=-1,w_2^{\prime }=1$，那就可以把它们排成一个matrix：$\left[\begin{array}{c}1-2\\ -11\end{array}\right]$，而我们的input又是一个2*1的vector：$\left[\begin{array}{c}1\\ -1\end{array}\right]$，将w和x相乘，再加上bias的vector：$\left[\begin{array}{c}1\\ 0\end{array}\right]$，就可以得到这一层的vector z，再经过activation function得到这一层的output：(activation function可以是很多类型的function，这里还是用Logistic Regression迁移过来的sigmoid function作为运算)
$$\sigma (\left[\begin{array}{c}1-2\\ -11\end{array}\right]\left[\begin{array}{c}1\\ -1\end{array}\right]+\left[\begin{array}{c}1\\ 0\end{array}\right])=\sigma (\left[\begin{array}{c}4\\ -2\end{array}\right])=\left[\begin{array}{c}0.98\\ 0.12\end{array}\right]$$

这里我们把所有的变量都以matrix的形式表示出来，注意$W^i$的matrix，每一行对应的是一个neuron的weight，行数就是neuron的个数，而input x，bias b和output y都是一个列向量，行数就是feature的个数(也是neuron的个数，neuron的本质就是把feature transform到另一个space)

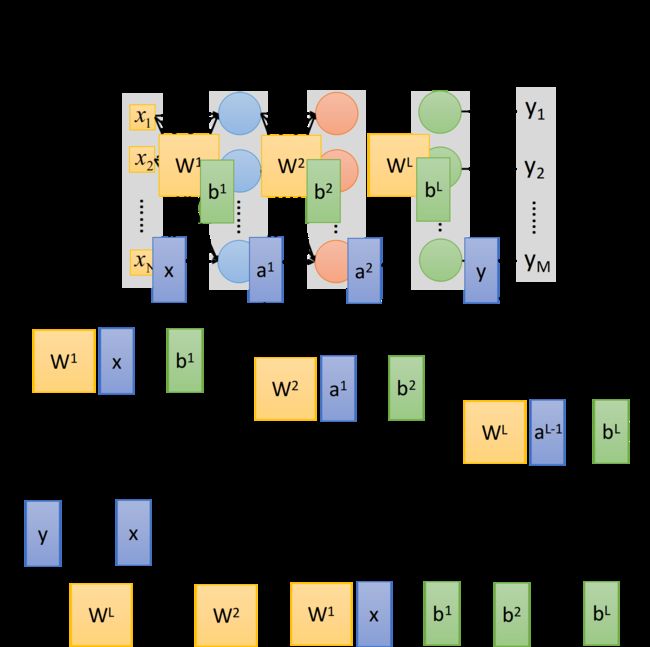
把这件事情写成矩阵运算的好处是，可以用GPU加速，GPU对matrix的运算是比CPU要来的快的，所以我们写neural network的时候，习惯把它写成matrix operation，然后call GPU来加速它

Output Layer

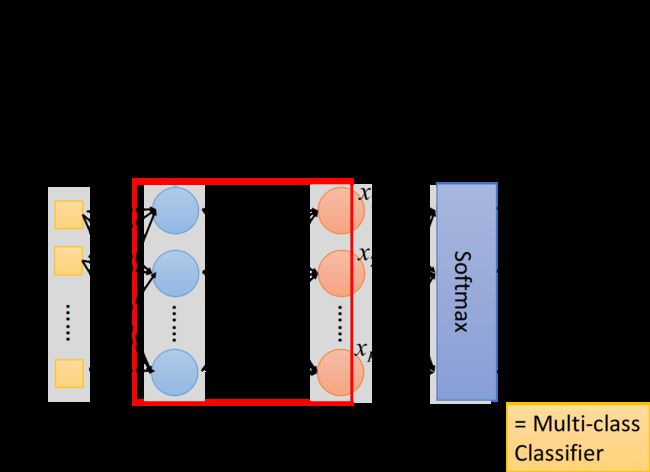
我们可以把hidden layers这部分，看做是一个feature extractor(特征提取器)，这个feature extractor就replace了我们之前手动做feature engineering，feature transformation这些事情，经过这个feature extractor得到的$x_1,x_2,...,x_k$就可以被当作一组新的feature

output layer做的事情，其实就是把它当做一个Multi-class classifier，它是拿经过feature extractor转换后的那一组比较好的feature(能够被很好地separate)进行分类的，由于我们把output layer看做是一个Multi-class classifier，所以我们会在最后一个layer加上softmax

Example Application

Handwriting Digit Recognition

这里举一个手写数字识别的例子，input是一张image，对机器来说一张image实际上就是一个vector，假设这是一张16*16的image，那它有256个pixel，对machine来说，它是一个256维的vector，image中的每一个都对应到vector中的一个dimension，简单来说，我们把黑色的pixel的值设为1，白色的pixel的值设为0

而neural network的output，如果在output layer使用了softmax，那它的output就是一个突出极大值的Probability distribution，假设我们的output是10维的话(10个数字，0~9)，这个output的每一维都对应到它可能是某一个数字的几率，实际上这个neural network的作用就是计算这张image成为10个数字的几率各自有多少，几率最大(softmax突出极大值的意义所在)的那个数字，就是机器的预测值

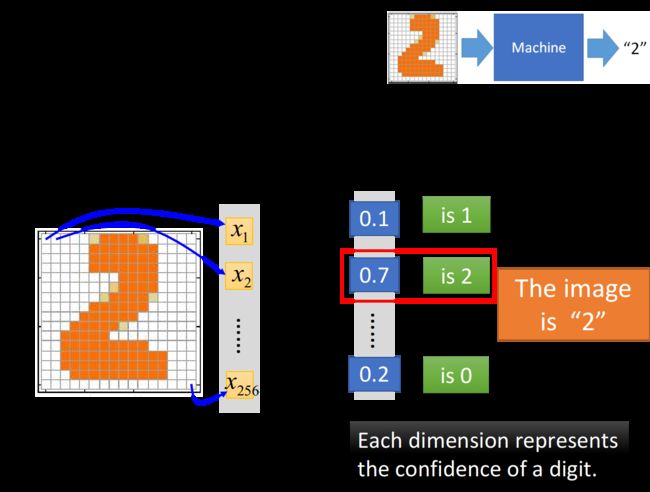
在这个手写字体识别的demo里，我们唯一需要的就是一个function，这个function的input是一个256的vector，output是一个10维的vector，这个function就是neural network(这里我们用简单的Feedforward network)

input固定为256维，output固定为10维的feedforward neural network，实际上这个network structure就已经确定了一个function set(model)的形状，在这个function set里的每一个function都可以拿来做手写数字识别，接下来我们要做的事情是用gradient descent去计算出一组参数，挑一个最适合拿来做手写数字识别的function

注：input、output的dimension，加上network structure，就可以确定一个model的形状，前两个是容易知道的，而决定这个network的structure则是整个Deep Learning中最为关键的步骤

所以这里很重要的一件事情是，我们要对network structure进行design，之前在做Logistic Regression或者是linear Regression的时候，我们对model的structure是没有什么好设计的，但是对neural network来说，我们现在已知的constraint只有input是256维，output是10维，而中间要有几个hidden layer，每个layer要有几个neuron，都是需要我们自己去设计的，它们近乎是决定了function set长什么样子

如果你的network structure设计的很差，这个function set里面根本就没有好的function，那就会像大海捞针一样，结果针并不在海里(滑稽

Step 1：Neural Network

256 dimension

10 dimension

input

network structure

output

input 256维，output 10维，以及自己design的network structure =》function set(model)

Step 2：Goodness of function

定义一个function的好坏，由于现在我们做的是一个Multi-class classification，所以image为数字1的label “1”告诉我们，现在的target是一个10维的vector，只有在第一维对应数字1的地方，它的值是1，其他都是0

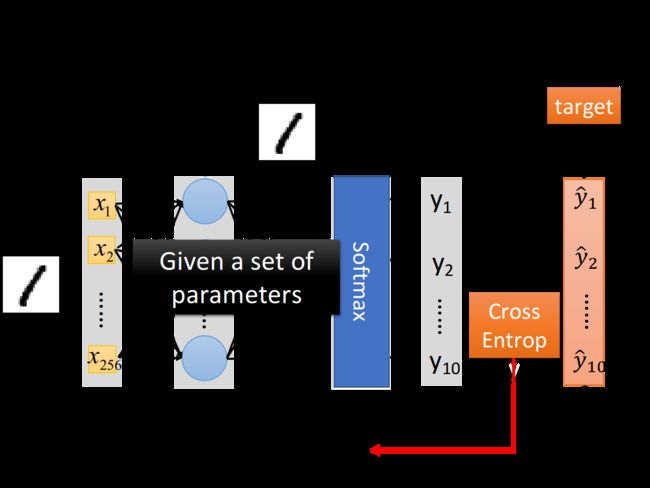
input这张image的256个pixel，通过这个neural network之后，会得到一个output，称之为y；而从这张image的label中转化而来的target，称之为$\hat{y}$，有了output $y$和target $\hat{y}$之后，要做的事情是计算它们之间的cross entropy(交叉熵)，这个做法跟我们之前做Multi-class classification的时候是一模一样的
$$CrossEntropy:l(y,\hat{y})=-\sum _{i=1}^{10}{\hat{y}}_{i}ln{y}_i$$

Step 3：Pick the best function

接下来就去调整参数，让这个cross entropy越小越好，当然整个training data里面不会只有一笔data，你需要把所有data的cross entropy都sum起来，得到一个total loss $L=\sum _{n=1}^N{l}^n$，得到loss function之后你要做的事情是找一组network的parameters：${\theta }^{\ast }$，它可以minimize这个total loss，这组parameter对应的function就是我们最终训练好的model

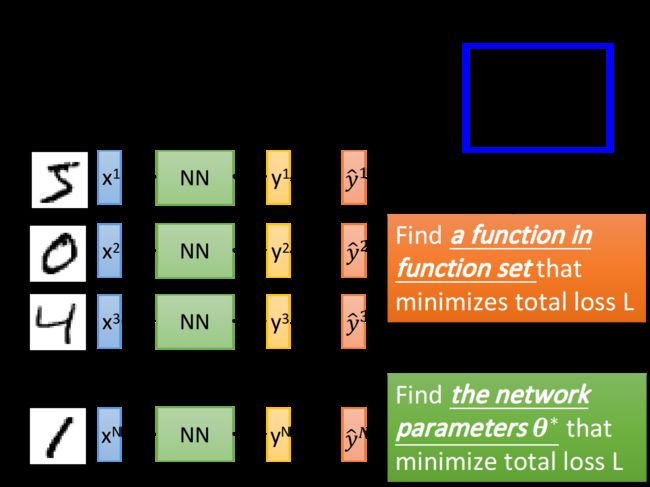
那怎么去找这个使total loss minimize的${\theta }^{\ast }$呢？使用的方法就是我们的老朋友——Gradient Descent

实际上在deep learning里面用gradient descent，跟在linear regression里面使用完全没有什么差别，只是function和parameter变得更复杂了而已，其他事情都是一模一样的

现在你的$\theta$里面是一大堆的weight、bias参数，先random找一个初始值，接下来去计算每一个参数对total loss的偏微分，把这些偏微分全部集合起来，就叫做gradient，有了这些偏微分以后，你就可以更新所有的参数，都减掉learning rate乘上偏微分的值，这个process反复进行下去，最终找到一组好的参数，就做完deep learning的training了

toolkit

你可能会问，这个gradient descent的function式子到底是长什么样子呢？之前我们都是一步一步地把那个算式推导出来的，但是在neural network里面，有成百上千个参数，如果要一步一步地人工推导并求微分的话是比较困难的，甚至是不可行的

其实，在现在这个时代，我们不需要像以前一样自己去implement Backpropagation(反向传播)，因为有太多太多的toolkit可以帮你计算Backpropagation，比如tensorflow、pytorch

注：Backpropagation就是算微分的一个比较有效的方式

something else

所以，其实deep learning就是这样子了，就算是alpha go，也是用gradient descent train出来的，可能在你的想象中它有多么得高大上，实际上就是在用gradient descent这样朴素的方法

有一些常见的问题：

Q：有人可能会问，机器能不能自动地学习network的structure？

• 其实是可以的，基因演算法领域是有很多的technique是可以让machine自动地去找出network structure，只不过这些方法目前没有非常普及

Q：我们可不可以自己去design一个新的network structure，比如说可不可以不要Fully connected layers(全连接层)，自己去DIY不同layers的neuron之间的连接？

• 当然可以，一个特殊的接法就是CNN(Convolutional Neural Network)，即卷积神经网络，这个下一章节会介绍