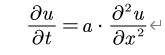基于热传导方程的高温作业专用服装设计（一）

基于热传导方程的高温作业专用服装设计（一）

此文为不才为备赛准备而已，若有先生雅正，不胜荣幸.
感谢，感谢……

摘要

本文以傅里叶定律、牛顿冷却定律为理论依据，主要研究高温作业专用服装的设计，建立了热传导模型，使用追赶法求解结果。
在问题一中，因为在传导过程中可以不计空气对流，将模型简化为一维热传导模型，并借助拉依达准则剔除异常数据，确保数据得精确性，并观察到题目分为稳态与非稳态两种情况。
对于一维稳态热传导模型，由热流密度函数求解出热流密度具体值，由温度分布函数求解出各介质的温度如下：

求解一维非稳态热传导问题模型，借助牛顿冷却定律、枚举法，确定空气与皮肤表面的转化系数，并将初值温度37度、左边界Dirichlet边值条件，右边界Robin边值条件，及基于临界面热流量密度和温度相等作为边界值条件使用，建立一维非稳态热传导问题模型。将连续定解区域作网格剖分，用隐式向后差分格式对原微分方程组离散化，得到三对角线性方程组，借助追赶法求解，得到时间与空间维度下的温度分布，见problem1.xlsx。通过查阅文献对差分方法进行对比分析，确定所选模型的精确性,对模型进行误差分析，定义偏差指数 f并求得其值为0.4593,最大误差1.99。
在问题二中，确定II介质的最优厚度，建立关于厚度的优化模型。在实际生产生活中，降低产品成本是首要考虑因素，制定II介质的最优厚度，实质上就是确定符合生产生活条件的最小厚度。使用问题一所建立的模型，根据问题二的要求对目标进行优化，利用循环遍历的枚举法，得出II介质的最小厚度为19.3mm，即II介质的最优厚度。
在问题三中，求Ⅱ、IV介质厚度的问题中，建立多目标优化模型。首先，从成本与穿着舒适度两方面，制定“最优”准则，并确定两个不同的优化目标；确定不同的权重之后，将双目标问题转化为单目标问题，可用问题二的循环遍历法继续求解，搜索出II介质的最优厚度为21.6mm，IV层介质的最优厚度为6.4mm。

关键字：傅里叶定律 隐式差分 追赶法 枚举法 多目标优化。

一、问题重述

在高温环境工作时，人需要穿着专用服装以避免灼伤。专用服装通常由三层织物材料构成，记为I、II、III层，其中I层与外界环境接触，III层与皮肤之间还存有空隙，将此空隙记为IV层。
为设计专用服装，将体内温度控制在37ºC的假人放置在实验室的高温环境中，测量假人皮肤外侧的温度。为了降低研发成本、缩短研发周期，请你们利用数学模型来确定假人皮肤外侧的温度变化情况，并解决以下问题：
（1）专用服装材料的某些参数值由附件1给出，对环境温度为75ºC、II层厚度为6 mm、IV层厚度为5 mm、工作时间为90分钟的情形开展实验，测量得到假人皮肤外侧的温度（见附件2）。建立数学模型，计算温度分布，并生成温度分布的Excel文件（文件名为problem1.xlsx）。
(2) 当环境温度为65ºC、IV层的厚度为5.5 mm时，确定II层的最优厚度，确保工作60分钟时，假人皮肤外侧温度不超过47ºC，且超过44ºC的时间不超过5分钟。
(3) 当环境温度为80 时，确定II层和IV层的最优厚度，确保工作30分钟时，假人皮肤外侧温度不超过47ºC，且超过44ºC的时间不超过5分钟。

二、问题分析

2.1问题一分析
问题一，根据假设建立一维热传导方程，建立基于热传导方程的温度分布模型，确定在一维空间中介质在不 同时刻，不同厚度下的温度。在模型建立时本文首先借助导热基本定律——傅里叶定律和能量守恒定律推导热传导方程。
数据处理之后，将题目分解为稳态与非稳态两种不同的形式。然后，求解一维稳态热传导问题模型，之后借助牛顿冷却定律，借助枚举法，确定空气与皮肤表面的转化系数，并将初值温度、左边界Dirichlet边值条件，右边界Robin边值条件，临界面热流量密度和温度相等作为边界值条件,建立维非稳态热传导问题模型，采用有限差分法中隐式差分方法进行模型求解，最后，对模型进行误差分析，定义偏差指数 f并求得其值为0.4593,最大误差1.99。
2.2问题二分析
问题二，确定II介质最优厚度是一个最优化问题，首先从服装成本与穿着舒适度两个方面讨论“最优"标准的制定，确定优化问题的目标为II层介质厚度最小。
其次，考虑问题二关于假人皮肤外侧温度的两个要求，同时结合问题–建立的基于热传导方程的温度分布模型，确定最优化问题的约束条件，从而建立II层最优厚度的单目标优化模型。
问题二模型的求解利用循环遍历的变步长枚举法，对II层介质的所有可能厚度进行遍历，求出满足约束条件的最小厚度。
2.3问题三分析
问题三，有两个变量，分别为Ⅱ和Ⅳ的厚度，相比于问题二增加了一个变量，所以求解Ⅱ，IV两层的最优厚度是一个多目标的优化问题。
通过查阅相关文献[1]得知，人体外表皮在温度大于44℃时开始发生热损伤，但是在此题中给出30分钟内不超过47℃，并且由于外表温度是单调非递减，所以必定在25分钟之后升至44℃。这可以作为问题三中的约束条件。
从服装成本与穿着舒适度两个方面考虑，分别制定出不同方面下的“最优”厚度标准，确定多目标优化问题的两个不同的目标。确定不同的权重之后，将双目标问题转化为单目标问题，可用问题二的循环遍历法继续求解。

三、模型假设

1、假设各层的介质都是均匀的，且保持各向同性；
2、假设热防护服的材质均匀无空隙，防护服与假人的形状抽象为嵌套合柱体；
3、假设各层介质的热传导率在各个方向一致；
4、假设外界环境无辐射；
5、忽略材料内部热源对模型的影响；
6、热传导沿垂直于皮肤方向进行，故系统可假设为一维模型。

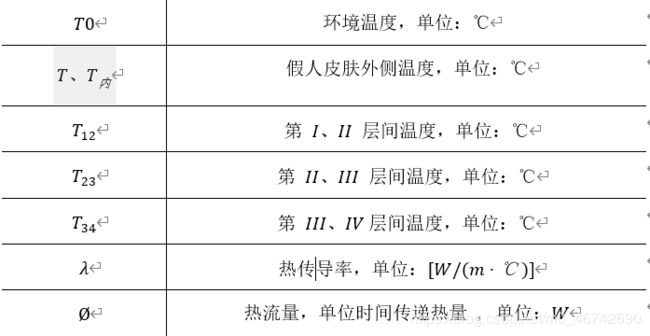
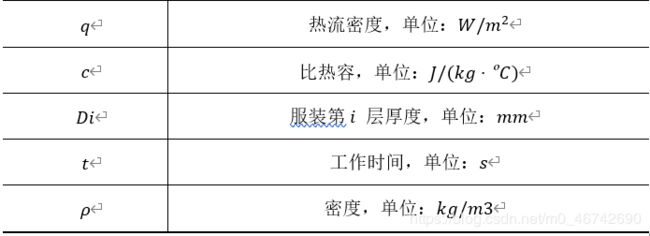
四、符号说明

五、问题一的模型建立与求解

5.1模型准备

5.1.1简化模型分析

高温作业专用服装的设计问题，实质上是将模糊现实问题转化为严谨数学模型，对参数进行数字化处理，以数学模型的优化设计，达到实际问题求解的目的。

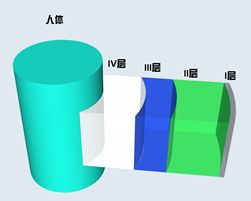
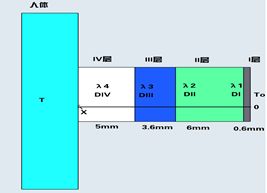
如图5.1.1所示，I层为材料层且与外界环境接触层，厚度0.6mm；II层为材料层，厚度6mm；III层为材料层，厚度为3.6mm；IV为与皮肤之间还存在空隙层，厚度为5mm；
易知，在高温作业服工作过程中，实际为空间温度的扩散过程，根据空间三维热传导方程[2]：

其中系数v > 0为介质的热扩散系数， 为已知热源函数。
可知，本题扩散过程与厚度、高度（防护服底部为基准面）、宽度有关，但因为在传导过程中可以不计空气对流，且不考虑人本身体积对模型影响，因此高度与宽度两维数将作为忽略量处理。即本题模型可近似看为只与厚度有关的一维平面模型。
一维热传导方程，即抛物型方程[2]为：

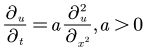
一维简化平面图如下：

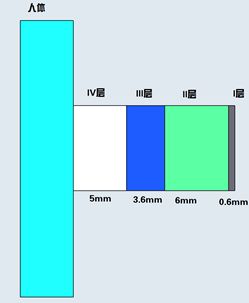
根据题意，环境温度为75ºC，体内温度37ºC。

5.1.2名词解释

温度分布[3]：
在给定时间的空间某区域内温度随空间位置的变化，一般地讲，物体的温度分布是坐标与时间的函数，即


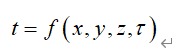
温度梯度：
沿等温线、等温面法线方向温度的增量与方向距离比值的极限称之为温 度梯度。
温度梯度为矢量，方向垂直于等温线，且指向温度增加的方向。

傅里叶定律：
单位时间通过一定截面的导热量，正比于垂直于截面的温度梯度和截面 面积。
热流量：

热流密度：
牛顿冷却定律：
牛顿冷却定律是温度高于周围环境的物体向周围媒质传递热量逐渐冷却 时所遵循的规律。具体的表述为：当物体表面与周围存在温差时，单位时间 从单位面积散失的热量与温度差成正比，比例系数为热传导率。
计算公式为：

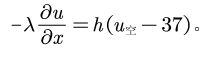
5.1.3数据处理与分析

拉依达准则剔除异常数据
附件二所示为皮肤外侧的测量温度随时间变化关系，为确保数据中无 可疑数据影响模型结果，对其进行拉依达准则剔除异常数据处理。
拉依达准则是指先假设一组检测数据只含有随机误差，对其进行计算处 理得到标准偏差，按一定概率确定一个区间，认为凡超过这个区间的误差， 就不属于随机误差而是粗大误差，含有该误差的数据应予以剔除。

时间与温度关系图分析
借助Matlab软件，将剔除异常数据过后的数据导入绘制时间-温度关系 图，如图5.1.3.1所示。
通过对温度随时间变化图像的分析，我们从中可以看出，温度在 t=0 时刻从接近人体体温的位置开始缓慢上升，直到达到48℃左右开始接近平 缓至稳定不变，那么我们可将温度场在时间维度上的变化分为两个阶段。 分析温度分布时将两种状态分开，即非稳态分析和稳态分析。
稳态：即是一个传热达到动态平衡，从宏观上讲温度在时间上基本达到 恒定的过程，那么我们可以初步考虑，试图用空间维度的角度，描述温度 场在 x 轴方向上的分布特点，其中可以采用逐层差分的方式构建方程，基 于稳态传热学相关理论进行合理的分析和求解。
非稳态：是一个变化的过程，因此可以 基于传热学的一些基本定律在时 间和空间两个维度上取微元 构建一维偏微分方程，运用数学物理方法中的 一些手段以及 Matlab相关化简及求数值解的算法，期望得到一个可描述非 稳态阶段的温度场函数T（x，t），并绘制出其空间曲面图。

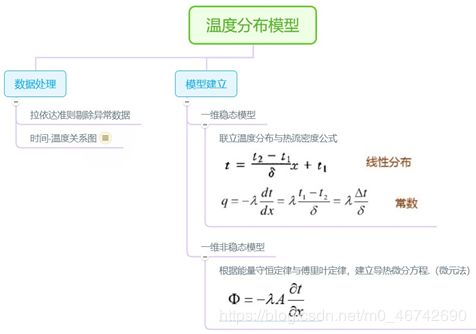
5.1.4模型流程图

根据假设建立一维温度分度模型，即建立根据距离x的变化，温度 的方程。
具体模型建立思路如下图5.2.1所示：

5.1.5导热问题的边界条件说明

5.2一维稳态热传导问题及其分析

5.3一维非稳态热传导问题及其分析

5.3.1热传导方程的推导

5.3.2定解问题条件建立一维非稳态热传导模型

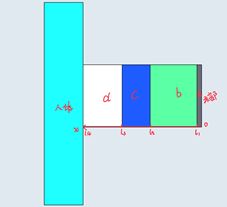
首先，建立所需的一维图解如图5.3.2.1，确定不同介质本身的热传导方程；
其次，根据在同一临界面具有相同的热流量密度与温度作为第二边界条件；
最后，根据牛顿冷却定律，给出Robin右边界条件，即可进行模型建立求解，如下图5.3.2.2所示。

Step1：确定介质a,b,c,d的热传导方程

Step2：第一、二边界条件定解条件运用


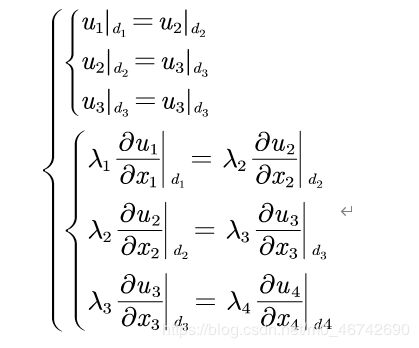
Step3：第三边界条件定解条件运用
已知外界温度为75°，并将热量传递给介质，又附件可得外界温度始终高于人体温度37°，进而在外界与人体热量交换过程中，符合牛顿冷却定律定义式，即是温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律。
依据牛顿冷却定律，给出 Robin 边界条件：

其中， 表示为介质d在贴近假人皮肤处的温度值； 表示为假人内部恒定温度，即 37°C,h为介质与皮肤之间的转化系数，即冷却系数。
在 t=0 时刻，介质 a,b,c,d的温度均与假人的恒定皮肤外侧温度相 同，即均为 37°，由此确定初值条件为：

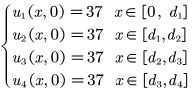
在x=0时，第I层与外界直接接触，温度为T0=75°

步骤3完整定解条件分析结果为：

Step4：转化系数h的确定
通过查阅资料可知，空气对流换热系数取值范围为
其次，通过附件 2 给出的不同时刻下假人皮肤表面的温度值，借助变步 长多次枚举法确定最佳转化系数的值。


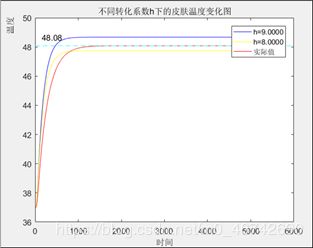
Step5：最终基于热传导方程的温度分布模型

5.3.3基于有限差分法的一维非稳态热传导模型求解[4]

一维非稳态热传导模型属于抛物型方程，因边值条件条件复杂难以求得 解析解，故本文采用有限差分法。
差分方法又称为有限差分方法或网格法，是求偏微分方程定解问题的数 值解中应用最广泛的方法之一。基本思想：将连续的定解区域用有限个离 散点构成的网格来代替；把定解区域上的连续变量的函数用网格上定义的 离散变量的函数来近似；把原方程和定解条件中的微商用差商来近似。最 终，把原微分方程和定解条件用代数方程组来代替，即有限差分方程组。 解此方程组就可以得到原问题在离散点上的近似值。
Step1:隐式差分格式方法的确定
在显示差分格式中，需满足求时间步长与空间步长的比 r 0.5 ，即时 间步长要比空间步长小得多。若不满足此条件，极易发生解的爆破。在本 文温度分布模型中，时间步长与空间步长达到 50，远远大于0.5，因此不适 合用显示差分格式，故本文选用隐式差分格式。
Step2:对求解区域进行网格剖分


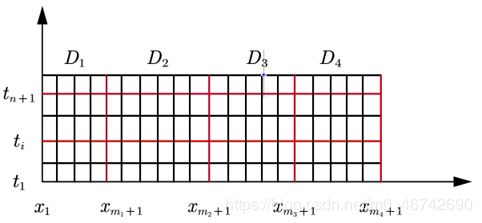
Step3:建立隐式差分格式




Step4:求隐式差分矩阵

Step5: 利用追赶法解三对角线性方程组[5]

5.3.4求解结果分析

四层介质的四个临界面相同时间间隔 下的温度值。绘制成温度关于时间的二维曲线，如下图5.2.1.1所示.

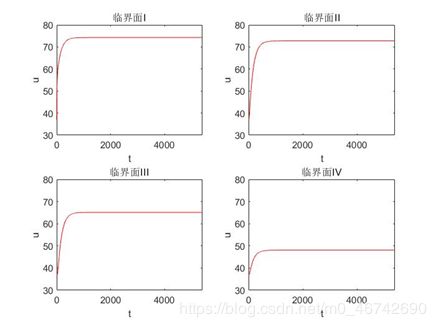
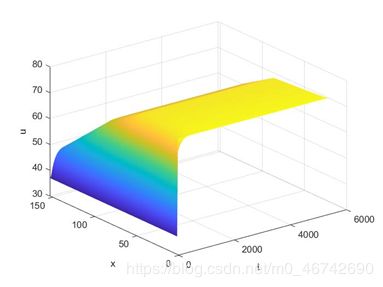
5.4差分格式精度分析[4]

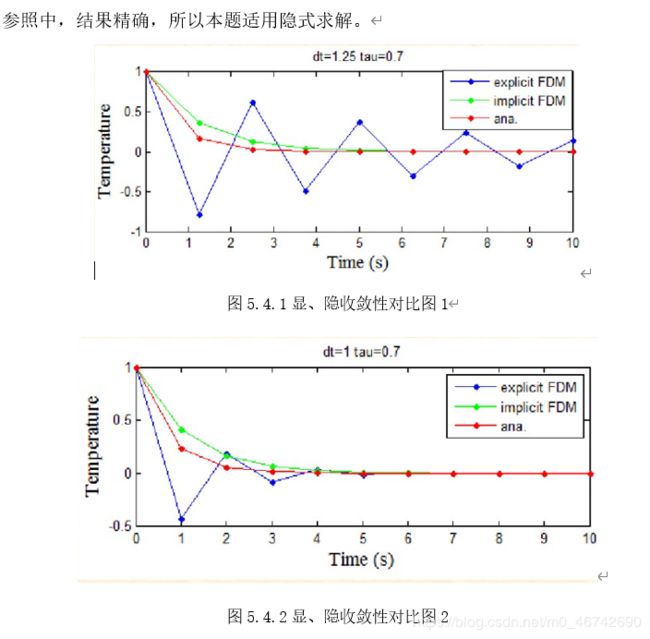
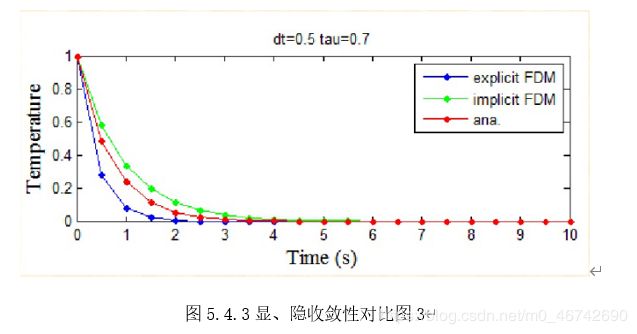
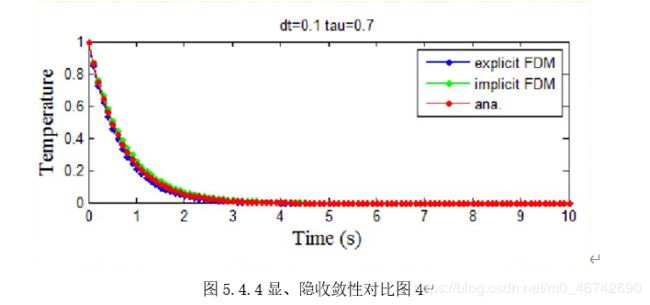
将 IV 层介质右侧与皮肤直接接触的临界面的温度与题目中附件2假人 皮肤外侧的测量温度进行对比，可检验求解结果的正确性。

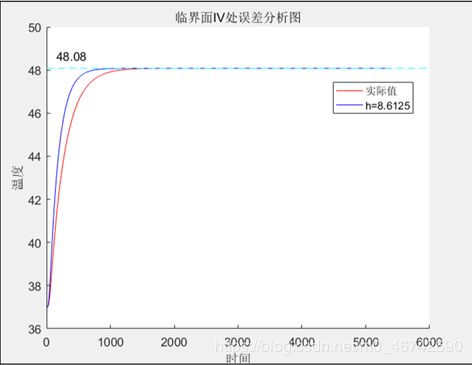
借用matalb编程得标准偏差f=0.4593，基本符合题意。

参考文献

[1] 潘斌.热防护服装热传递数学建模及参数决定反问题[D].浙江理工大学.2016.12.28
[2]司守奎.数学建模方法与应用[M].北京:国防大学出版社，1994年:360页~370页.
[3]靳涛.高温作业专用服装的温度分布模型[J].消防界(电子版),2020, 6(10):
24-28.
[4]zzlghust.第二章-稳态热传导[Z].@百度文库,2018.
[5]zhangchao3322218.追赶法解三对角线性方程组(Matlab)[Z]. @CSDN,2011.

clear;%清除工作区变量
clc;%清屏
close all;%关闭所有图形窗口

z=[];
h=8.6125; %空气交换系数
%% 材料参数输入
m1=6;m2=60;m3=36;m4=50;% 分别对四种介质分割
m=m1+m2+m3+m4;% 介质分割和
n=5400;% 对时间分割
t=5400;% 总时长
l1=0.6/1000;l2=6/1000;l3=3.6/1000;l4=5/1000;% 四种材料厚度
lam_1=0.082;lam_2=0.37;lam_3=0.045;lam_4=0.028;% 四种材料的热传导率
de_1=300;de_2=862;de_3=74.2;de_4=1.18;% 四种材料的密度
c1=1377;c2=2100;c3=1726;c4=1005;% 四种材料的比热容

%% 计算热扩散率
a1=lam_1/(c1*de_1);% I层材料的热扩散率
a2=lam_2/(c2*de_2);% II层材料的热扩散率
a3=lam_3/(c3*de_3);% III层材料的热扩散率
a4=lam_4/(c4*de_4);% IV层材料的热扩散率

%% 材料长度分割和时间步长分割求解
derta_x1=l1/m1;% I层材料的分割长度
derta_x2=l2/m2;% II层材料的分割长度
derta_x3=l3/m3;% III层材料的分割长度
derta_x4=l4/m4;% IV层材料的分割长度
derta_t=t/n;% 时间步长分割

%% 计算各层介质剖分的步长比
r1=derta_t/derta_x1^2*a1;% 第I层介质剖分的步长比
r2=derta_t/derta_x2^2*a2;% 第II层介质剖分的步长比
r3=derta_t/derta_x3^2*a3;% 第III层介质剖分的步长比
r4=derta_t/derta_x4^2*a4;% 第IV层介质剖分的步长比

u=zeros(m+1,n+1);% 定义四层耦合介质温度分布矩阵
%% 初始条件和边界条件
u(:,1)=37;%初始条件
u(1,:)=75;%边界条件

%% 差分格式的系数矩阵的构造
A=zeros(m,m);
for i=1:m1-1
 A(i,i)=1+2*r1;
 A(i,i+1)=-r1;
if i>=2
A(i,i-1)=-r1;
end
end
A(m1,m1)=(lam_1/derta_x1+lam_2/derta_x2);
A(m1,m1-1)=-lam_1/derta_x1;
A(m1,m1+1)=-lam_2/derta_x2;

for i=m1+1:m1+m2-1
A(i,i)=1+2*r2;
 A(i,i+1)=-r2;    
A(i,i-1)=-r2;
end
A(m1+m2,m1+m2)=(lam_2/derta_x2+lam_3/derta_x3);
A(m1+m2,m1+m2-1)=-lam_2/derta_x2;
A(m1+m2,m1+m2+1)=-lam_3/derta_x3;

for i=m1+m2+1:m1+m2+m3-1
A(i,i)=1+2*r3;
 A(i,i+1)=-r3;    
A(i,i-1)=-r3;
end
A(m1+m2+m3,m1+m2+m3)=(lam_3/derta_x3+lam_4/derta_x4);
A(m1+m2+m3,m1+m2+m3-1)=-lam_3/derta_x3;
A(m1+m2+m3,m1+m2+m3+1)=-lam_4/derta_x4;

for i=m1+m2+m3+1:m1+m2+m3+m4-1
A(i,i)=1+2*r4;
A(i,i-1)=-r4;
 A(i,i+1)=-r4;    
end
A(m,m)=h+lam_4/derta_x4;
A(m,m-1)=-lam_4/derta_x4;

%% 构造右端项
for k=2:n+1 
b=zeros(m,1);
for i=2:m-1
b(i,1)=u(i+1,k-1);
end
b(1,1)=u(2,k-1)+r1*u(1,k);
b(m1,1)=0;
b(m1+m2,1)=0;
b(m1+m2+m3,1)=0;
b(m,1)=37*h;

%% 追赶法求解
bb=diag(A)';
aa=[0,diag(A,-1)'];
c=diag(A,1)';
N=length(bb);
L=zeros(N);
uu0=0;y0=0;aa(1)=0;
L(1)=bb(1)-aa(1)*uu0;
y(1)=(b(1)-y0*aa(1))/L(1);
uu(1)=c(1)/L(1);
for i=2:(N-1)
L(i)=bb(i)-aa(i)*uu(i-1);
y(i)=(b(i)-y(i-1)*aa(i))/L(i);
uu(i)=c(i)/L(i);
end
L(N)=bb(N)-aa(N)*uu(N-1);
y(N)=(b(N)-y(N-1)*aa(N))/L(N);
x(N)=y(N);
for i=(N-1):-1:1
x(i)=y(i)-uu(i)*x(i+1);
end
u(2:m+1,k)=x';
end

%% 绘制不同时刻不同厚度温度分布图
x=1:1:m+1;
t=1:1:t+1;
surf(t,x,u)
shading interp
xlabel('t')
ylabel('x')
zlabel('u')

u=round(u,2);
xlswrite('不同时间不同厚度下的温度分布.xlsx',u)% 生成温度分布的excle文件

%% 四个临界面下的部分温度分布表
U=zeros(5401,4);
U(:,1)=u(m1+1,:)';
U(:,2)=u(m1+m2+1,:)';
U(:,3)=u(m1+m2+m3+1,:)';
U(:,4)=u(m1+m2+m3+m4+1,:)';

xlswrite('problem1.xlsx',U)% 存储生成四个临界面下的部分温度分布表于problem1

figure
subplot(2,2,1)
plot(U(:,1),'r')
xlabel('t');ylabel('u');
title('临界面I')
axis([0 5400 30 80])
subplot(2,2,2)
plot(U(:,2),'r')
xlabel('t');ylabel('u');
title('临界面II')
axis([0 5400 30 80])
subplot(2,2,3)
plot(U(:,3),'r')
title('临界面III')
axis([0 5400 30 80])
xlabel('t');ylabel('u');
subplot(2,2,4)
plot(U(:,4),'r')
title('临界面IV')
axis([0 5400 30 80])
xlabel('t');ylabel('u');

求解空气系数范围

clear;%清除工作区变量
clc;%清屏
close all;%关闭所有图形窗口

z=[];
for h=8:0.01:9 %确定空气交换系数范围
%% 材料参数输入
m1=6;m2=60;m3=36;m4=50;% 分别对四种介质分割
m=m1+m2+m3+m4;% 介质分割和
n=5400;% 对时间分割
t=5400;% 总时长
l1=0.6/1000;l2=6/1000;l3=3.6/1000;l4=5/1000;% 四种材料厚度
lam_1=0.082;lam_2=0.37;lam_3=0.045;lam_4=0.028;% 四种材料的热传导率
de_1=300;de_2=862;de_3=74.2;de_4=1.18;% 四种材料的密度
c1=1377;c2=2100;c3=1726;c4=1005;% 四种材料的比热容

%% 计算热扩散率
a1=lam_1/(c1*de_1);% I层材料的热扩散率
a2=lam_2/(c2*de_2);% II层材料的热扩散率
a3=lam_3/(c3*de_3);% III层材料的热扩散率
a4=lam_4/(c4*de_4);% IV层材料的热扩散率

%% 材料长度分割和时间步长分割求解
derta_x1=l1/m1;% I层材料的分割长度
derta_x2=l2/m2;% II层材料的分割长度
derta_x3=l3/m3;% III层材料的分割长度
derta_x4=l4/m4;% IV层材料的分割长度
derta_t=t/n;% 时间步长分割

%% 计算各层介质剖分的步长比
r1=derta_t/derta_x1^2*a1;% 第I层介质剖分的步长比
r2=derta_t/derta_x2^2*a2;% 第II层介质剖分的步长比
r3=derta_t/derta_x3^2*a3;% 第III层介质剖分的步长比
r4=derta_t/derta_x4^2*a4;% 第IV层介质剖分的步长比

u=zeros(m+1,n+1);% 定义四层耦合介质温度分布矩阵
%% 初始条件和边界条件
u(:,1)=37;%初始条件
u(1,:)=75;%边界条件

%% 差分格式的系数矩阵的构造
A=zeros(m,m);
for i=1:m1-1
 A(i,i)=1+2*r1;
 A(i,i+1)=-r1;
if i>=2
A(i,i-1)=-r1;
end
end
A(m1,m1)=(lam_1/derta_x1+lam_2/derta_x2);
A(m1,m1-1)=-lam_1/derta_x1;
A(m1,m1+1)=-lam_2/derta_x2;

for i=m1+1:m1+m2-1
A(i,i)=1+2*r2;
 A(i,i+1)=-r2;    
A(i,i-1)=-r2;
end
A(m1+m2,m1+m2)=(lam_2/derta_x2+lam_3/derta_x3);
A(m1+m2,m1+m2-1)=-lam_2/derta_x2;
A(m1+m2,m1+m2+1)=-lam_3/derta_x3;

for i=m1+m2+1:m1+m2+m3-1
A(i,i)=1+2*r3;
 A(i,i+1)=-r3;    
A(i,i-1)=-r3;
end
A(m1+m2+m3,m1+m2+m3)=(lam_3/derta_x3+lam_4/derta_x4);
A(m1+m2+m3,m1+m2+m3-1)=-lam_3/derta_x3;
A(m1+m2+m3,m1+m2+m3+1)=-lam_4/derta_x4;

for i=m1+m2+m3+1:m1+m2+m3+m4-1
A(i,i)=1+2*r4;
A(i,i-1)=-r4;
 A(i,i+1)=-r4;    
end
A(m,m)=h+lam_4/derta_x4;
A(m,m-1)=-lam_4/derta_x4;

%% 构造右端项
for k=2:n+1 
b=zeros(m,1);
for i=2:m-1
b(i,1)=u(i+1,k-1);
end
b(1,1)=u(2,k-1)+r1*u(1,k);
b(m1,1)=0;
b(m1+m2,1)=0;
b(m1+m2+m3,1)=0;
b(m,1)=37*h;

%% 追赶法求解
bb=diag(A)';
aa=[0,diag(A,-1)'];
c=diag(A,1)';
N=length(bb);
L=zeros(N);
uu0=0;y0=0;aa(1)=0;
L(1)=bb(1)-aa(1)*uu0;
y(1)=(b(1)-y0*aa(1))/L(1);
uu(1)=c(1)/L(1);
for i=2:(N-1)
L(i)=bb(i)-aa(i)*uu(i-1);
y(i)=(b(i)-y(i-1)*aa(i))/L(i);
uu(i)=c(i)/L(i);
end
L(N)=bb(N)-aa(N)*uu(N-1);
y(N)=(b(N)-y(N-1)*aa(N))/L(N);
x(N)=y(N);
for i=(N-1):-1:1
x(i)=y(i)-uu(i)*x(i+1);
end
u(2:m+1,k)=x';
end

%% 绘制h=8和h=9的皮肤温度变换图
if h==8
B1=u(m+1,:);
plot(B1,'color','b');
hold on  
end
if h==9
C1=u(m+1,:);
plot(C1,'color','y') ;
end
q=u(m+1,t+1)-48.08;
z=[z q];
[d p]=min(abs(z));
end

fprintf('空气系数范围：\n')
fprintf('%.2f---%.2f\n',8+(p-1)*0.01,8+(p+1)*0.01)

A1=xlsread('CUMCM-2018-Problem-A-Chinese-Appendix.xlsx',2,'B3:B5403');
plot(A1,'color','r')

title('不同转化系数h下的皮肤温度变化图')
xlabel('时间')
ylabel('温度') 

legend('h=9.0000','h=8.0000','实际值')
x=0:1:6000;y1=48.08*ones(6001,1);
plot(x,y1,'--','color','c')
text(150.6685,48.6752,'48.08')

求解空气系数

clear;%清除工作区变量
clc;%清屏
close all;%关闭所有图形窗口

z=[];
for h=8.61:0.0001:8.63 %确定空气交换系数
%% 材料参数输入
m1=6;m2=60;m3=36;m4=50;% 分别对四种介质分割
m=m1+m2+m3+m4;% 介质分割和
n=5400;% 对时间分割
t=5400;% 总时长
l1=0.6/1000;l2=6/1000;l3=3.6/1000;l4=5/1000;% 四种材料厚度
lam_1=0.082;lam_2=0.37;lam_3=0.045;lam_4=0.028;% 四种材料的热传导率
de_1=300;de_2=862;de_3=74.2;de_4=1.18;% 四种材料的密度
c1=1377;c2=2100;c3=1726;c4=1005;% 四种材料的比热容

%% 计算热扩散率
a1=lam_1/(c1*de_1);% I层材料的热扩散率
a2=lam_2/(c2*de_2);% II层材料的热扩散率
a3=lam_3/(c3*de_3);% III层材料的热扩散率
a4=lam_4/(c4*de_4);% IV层材料的热扩散率

%% 材料长度分割和时间步长分割求解
derta_x1=l1/m1;% I层材料的分割长度
derta_x2=l2/m2;% II层材料的分割长度
derta_x3=l3/m3;% III层材料的分割长度
derta_x4=l4/m4;% IV层材料的分割长度
derta_t=t/n;% 时间步长分割

%% 计算各层介质剖分的步长比
r1=derta_t/derta_x1^2*a1;% 第I层介质剖分的步长比
r2=derta_t/derta_x2^2*a2;% 第II层介质剖分的步长比
r3=derta_t/derta_x3^2*a3;% 第III层介质剖分的步长比
r4=derta_t/derta_x4^2*a4;% 第IV层介质剖分的步长比

u=zeros(m+1,n+1);% 定义四层耦合介质温度分布矩阵
%% 初始条件和边界条件
u(:,1)=37;%初始条件
u(1,:)=75;%边界条件

%% 差分格式的系数矩阵的构造
A=zeros(m,m);
for i=1:m1-1
 A(i,i)=1+2*r1;
 A(i,i+1)=-r1;
if i>=2
A(i,i-1)=-r1;
end
end
A(m1,m1)=(lam_1/derta_x1+lam_2/derta_x2);
A(m1,m1-1)=-lam_1/derta_x1;
A(m1,m1+1)=-lam_2/derta_x2;

for i=m1+1:m1+m2-1
A(i,i)=1+2*r2;
 A(i,i+1)=-r2;    
A(i,i-1)=-r2;
end
A(m1+m2,m1+m2)=(lam_2/derta_x2+lam_3/derta_x3);
A(m1+m2,m1+m2-1)=-lam_2/derta_x2;
A(m1+m2,m1+m2+1)=-lam_3/derta_x3;

for i=m1+m2+1:m1+m2+m3-1
A(i,i)=1+2*r3;
 A(i,i+1)=-r3;    
A(i,i-1)=-r3;
end
A(m1+m2+m3,m1+m2+m3)=(lam_3/derta_x3+lam_4/derta_x4);
A(m1+m2+m3,m1+m2+m3-1)=-lam_3/derta_x3;
A(m1+m2+m3,m1+m2+m3+1)=-lam_4/derta_x4;

for i=m1+m2+m3+1:m1+m2+m3+m4-1
A(i,i)=1+2*r4;
A(i,i-1)=-r4;
A(i,i+1)=-r4;    
end
A(m,m)=h+lam_4/derta_x4;
A(m,m-1)=-lam_4/derta_x4;

%% 构造右端项
for k=2:n+1 
b=zeros(m,1);
for i=2:m-1
b(i,1)=u(i+1,k-1);
end
b(1,1)=u(2,k-1)+r1*u(1,k);
b(m1,1)=0;
b(m1+m2,1)=0;
b(m1+m2+m3,1)=0;
b(m,1)=37*h;

%% 追赶法求解
bb=diag(A)';
aa=[0,diag(A,-1)'];
c=diag(A,1)';
N=length(bb);
L=zeros(N);
uu0=0;y0=0;aa(1)=0;
L(1)=bb(1)-aa(1)*uu0;
y(1)=(b(1)-y0*aa(1))/L(1);
uu(1)=c(1)/L(1);
for i=2:(N-1)
L(i)=bb(i)-aa(i)*uu(i-1);
y(i)=(b(i)-y(i-1)*aa(i))/L(i);
uu(i)=c(i)/L(i);
end
L(N)=bb(N)-aa(N)*uu(N-1);
y(N)=(b(N)-y(N-1)*aa(N))/L(N);
x(N)=y(N);
for i=(N-1):-1:1
x(i)=y(i)-uu(i)*x(i+1);
end
u(2:m+1,k)=x';
end
q=u(m+1,t+1)-48.08;
z=[z q];
[d p]=min(abs(z));
end

fprintf('空气交换系数：\n')
fprintf('    %.4f\n',8.61+0.0001*p)

链接：https://pan.baidu.com/s/1DhKwv8OECyCAWAbbubkGYQ
提取码：qelh