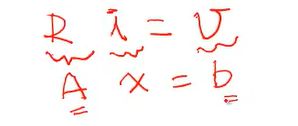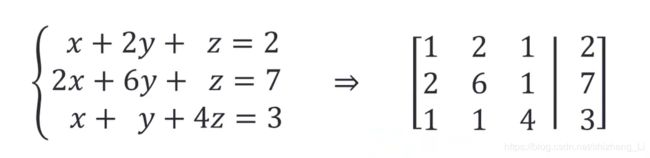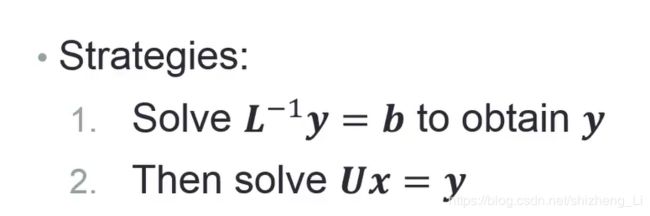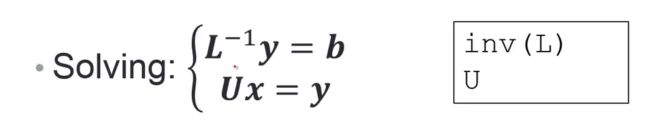台湾国立大学郭彦甫Matlab教程笔记（21）linear equations(高斯消去法和追赶法)

台湾国立大学郭彦甫Matlab教程笔记（21）

today:
linear equation 线性方程
linear system 线性系统

我们先看第一部分

linear equation

假定一个线性方程组：

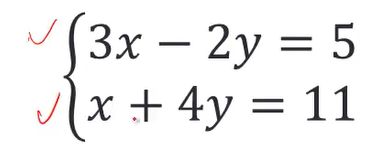
下面我们用矩阵的形式表示这个二元一次方程组：Ax=b的形式

WHy matrix form？

可能多元，问题本身很复杂，矩阵方法可以通吃。
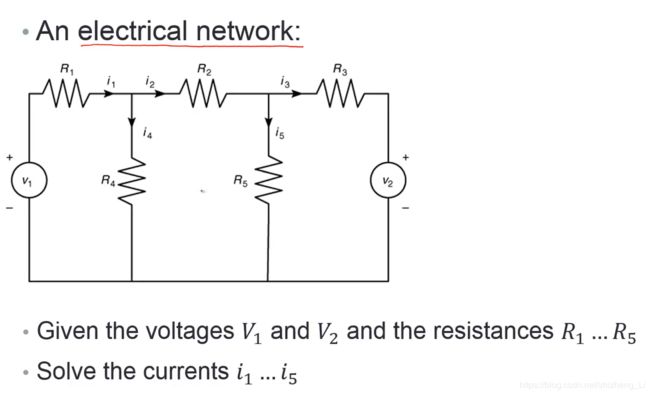
下面是一道电路题目：给定电源电压和电阻值，求解电流值是多少

老师口中的tilde 是波浪线的意思

这道题目的求解需要用到基尔霍夫电流定律和基尔霍夫电压定律，这里不详细展开
基尔霍夫电压定律 voltage law：一个回路电压和为零
基尔霍夫电流定律 current law：一个节点的流入电流和流出电流代数和为0

列出来的线性方程组如下：

我们需要求解是i，转化成矩阵是这样的形式：

得到的矩阵为：

usually when solving linear equations:
1.
A and b are known
2.
x is unknown

solving linear equations求解线性方程

两类方法：
1.消去法 successive elimination (through factorization)
2.克拉姆法则(Cramer’s method)

第一类消去法里面又分类

第一种：高斯消去法Gaussian Elimination

例题：

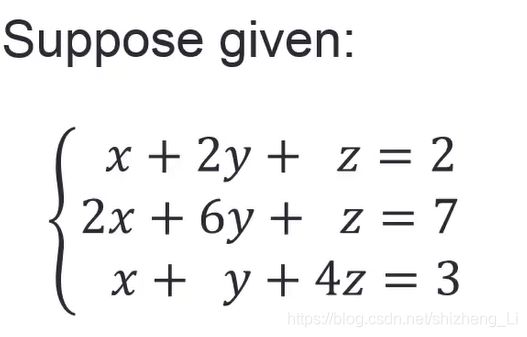
把方程组写成矩阵的形式，增广矩阵

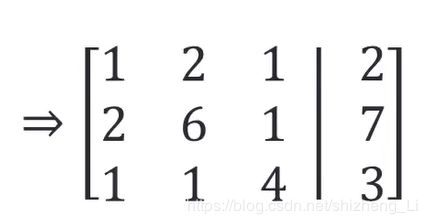
利用矩阵的性质，第一行*（-2）加到第二行中，第一行乘以（-1）加到第三行中，得到下面的矩阵（行列式，矩阵的化简，多出现0，便于计算和分析）下图得到上三角

这样就可以计算出来x3等于多少 ，x3=1（只看第三行）
然后把x3=1带入到第二个方程，解出来x2，然后再代入到第一个方程，解出来x1

这个过程就是高斯消去法的思路

下面我们看在matlab中如何使用Gaussian Elimination

Gaussian Elimination --rref()

首先把方程组表示成为增广矩阵的形式

代码表示：
[A b]表示的是一个增广矩阵

A=[1 2 1 ;2 6 1;1 1 4];
b=[2;7;3];
R=rref([A b])

我们执行这段代码看看这个方程组解的情况：

以上表示x1=-3；x2=2;x3=1;也就是方程组的解

接着看下一个消去的方法：

LU Factorization追赶法

这个是我一篇博文里记录的：追赶法
factorization 是因数分解的意思
L：lower-triangular matrix下三角矩阵
U：upper-triangular matrix上三角矩阵
思路是把A矩阵拆分成两个三角阵

两个三角阵是这样的形式：A等于L的逆矩阵乘以U矩阵

因式分解矩阵的目的是：把L的inverse 乘以U代入得到下式，然后把Ux令为y，然后解的问题就转化为：先求y，然后求x。
这样处理，因为三角行列式有一半是0，求解起来变得简单。

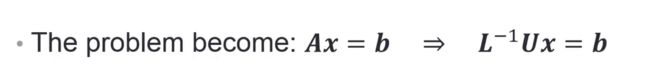
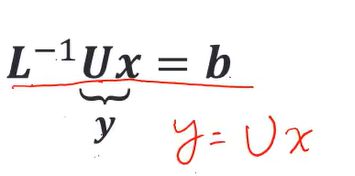
知道追赶法的原理了，我们现在来看一下下三角矩阵和上三角矩阵

下面的问题是：如何得到这个L和U矩阵呢？
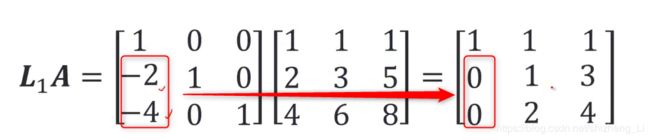
下图中左边乘以很多Li，最终是让右边成为一个上三角矩阵（左下角全为零），这些L的目的是一列一列的来计算，一列一列的让其变成零

通过矩阵乘法，左边乘
A=inv（L）U
LA=Linv（L）*U
LA=U

怎么算呢？举个例子

给定一个A矩阵

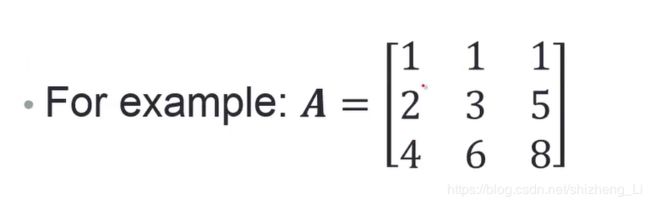
解体过程：
因为A左边乘的是一个下三角矩阵，其主对角线上的元素全为1，右上角全为零。
现在，让L左下角等于什么，使得运算完成只有右边U的第一列为零？

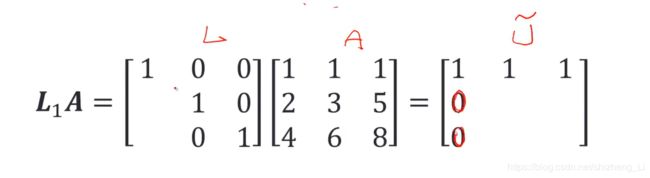
求解：u（2，1）是L的第二行A的第一列得到的结果，可以求得 L（2，1）=-2
同理u（3,1）=L的第三行A的第一列，可以求得L（3，1）=-4
所以，把这两个数放进去，计算

然后以此类推：L1A左边还要乘以L2（也是一个下三角矩阵：对角线还是1）

L2（3，2）需要填什么使得右边U第二列下面也变成零（使之不断朝向上三角矩阵靠近）
同理，L2（3，2）=-2
这样就算出来U上三角矩阵长什么样子

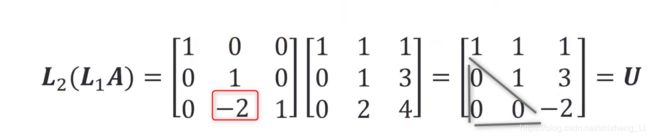
而且，我们有了L2和L1，所有下三角矩阵也有了 L=L2*L1

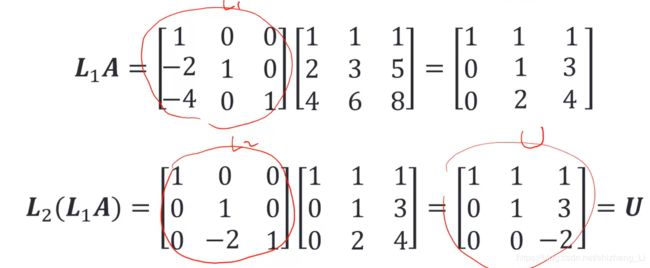
下一步呢？
算出来L的inverse， 和b矩阵，来求y矩阵

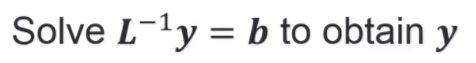
求出来y之后，用u矩阵和y矩阵来求x即可。

通过以上具体的例子，读者肯定对这个追赶法（上下三角分解法）的原理有了进一步的认识。
下面就看matlab中具体指令是怎么样的

LU Factorization -lu()函数

还是这个矩阵A,矩阵b

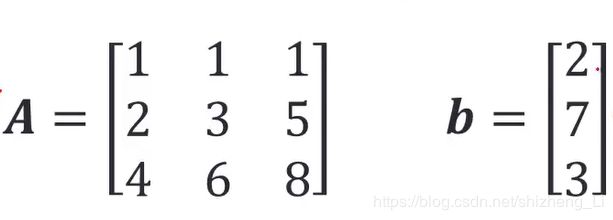
A=[1 1 1;2 3 5 ; 4 6 8];
[L,U,P]=lu(A);
通过函数lu()可以求出原矩阵的上三角矩阵U和下三角阵L
然后：
inv(L)%L矩阵的逆矩阵

算出来，上面两个式子：

下面笔者实操一下看看具体的matlab实现过程：

代码：
A=[1 1 1;2 3 5 ; 4 6 8];
[L,U,P]=lu(A)%得到下三角矩阵和上三角阵
得到的结果：

然后需要求inv(L)
invL=inv(L)
求得结果：

然后需要invL*y=b来求解，需要回顾前面老师讲的线性方程组的求法：高斯消去法rref()函数
当然要输入进来b矩阵 b=[1 2 7]’

用高斯消去法求解y
y=rref([invL,b])
求得y矩阵：

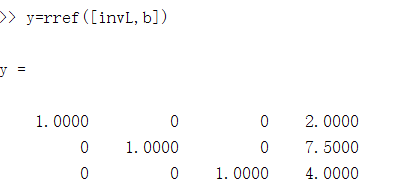
同样的道理，高斯消去法求解x矩阵
这里y的解分别是y1=2,y2=7.5,y3=4;
需要重新整理y矩阵，得到y的解矩阵

y1=y(:,4)
结果：

然后求解x
x=rref([U,y1])
得到x的结果：

x1=x(:,4)

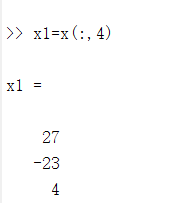
笔者：上次参加上海市数学建模培训时候，2018年A题关于防热服的题目，其中关于矩阵的运算用到了追赶法，因为数据量比较大，得到的线性方程组很多，计算量很大，直接来高斯消去法很慢或者解不出来，老师讲到的数据处理的技巧就是追赶法的应用。

希望读者好好体会这个追赶法的使用，可以很好的简化计算的复杂度，尤其是数据量很大的时候。

【总结一下】
本文记录了线性方程组的一些解法。
【1】高斯消去法rref()函数。
【2】追赶法：上下三角阵：Ax=b ,A =inv(L)U
得到 y=Ux
先求解：inv(L)*y=b
再求解：Ux=y