SDOI 2008 洞穴勘测

Description

　　辉辉热衷于洞穴勘测。某天，他按照地图来到了一片被标记为JSZX的洞穴群地区。经过初步勘测，辉辉发现这片区域由n个洞穴（分别编号为1到n）以及若干通道组成，并且每条通道连接了恰好两个洞穴。假如两个洞穴可以通过一条或者多条通道按一定顺序连接起来，那么这两个洞穴就是连通的，按顺序连接在一起的这些通道则被称之为这两个洞穴之间的一条路径。
　　洞穴都十分坚固无法破坏，然而通道不太稳定，时常因为外界影响而发生改变，比如，根据有关仪器的监测结果，123号洞穴和127号洞穴之间有时会出现一条通道，有时这条通道又会因为某种稀奇古怪的原因被毁。辉辉有一台监测仪器可以实时将通道的每一次改变状况在辉辉手边的终端机上显示：
　　如果监测到洞穴u和洞穴v之间出现了一条通道，终端机上会显示一条指令 Connect u v
　　如果监测到洞穴u和洞穴v之间的通道被毁，终端机上会显示一条指令 Destroy u v
　　经过长期的艰苦卓绝的手工推算，辉辉发现一个奇怪的现象：无论通道怎么改变，任意时刻任意两个洞穴之间至多只有一条路径。因而，辉辉坚信这是由于某种本质规律的支配导致的。因而，辉辉更加夜以继日地坚守在终端机之前，试图通过通道的改变情况来研究这条本质规律。
　　然而，终于有一天，辉辉在堆积成山的演算纸中崩溃了……他把终端机往地面一砸（终端机也足够坚固无法破坏），转而求助于你，说道：“你老兄把这程序写写吧”。
　　辉辉希望能随时通过终端机发出指令 Query u v，向监测仪询问此时洞穴u和洞穴v是否连通。现在你要为他编写程序回答每一次询问。
　　已知在第一条指令显示之前，JSZX洞穴群中没有任何通道存在。

Input

　　第一行为两个正整数n和m，分别表示洞穴的个数和终端机上出现过的指令的个数。
　　以下m行，依次表示终端机上出现的各条指令。每行开头是一个表示指令种类的字符串s（"Connect”、”Destroy”或者”Query”，区分大小写），之后有两个整数u和v (1≤u, v≤n且u≠v) 分别表示两个洞穴的编号。

Output

　　对每个Query指令，输出洞穴u和洞穴v是否互相连通：是输出”Yes”，否则输出”No”。（不含双引号）

Sample Input

200 5

Query 123 127

Connect 123 127

Query 123 127

Destroy 127 123

Query 123 127

Sample Output

No

Yes

No

Hint

【样例2】
样例输入（cave.in文件内容）：
3 5
Connect 1 2
Connect 3 1
Query 2 3
Destroy 1 3
Query 2 3

样例输出（cave.out文件内容）：
Yes
No
【数据范围】
10%的数据满足n≤1000, m≤20000
20%的数据满足n≤2000, m≤40000
30%的数据满足n≤3000, m≤60000
40%的数据满足n≤4000, m≤80000
50%的数据满足n≤5000, m≤100000
60%的数据满足n≤6000, m≤120000
70%的数据满足n≤7000, m≤140000
80%的数据满足n≤8000, m≤160000
90%的数据满足n≤9000, m≤180000
100%的数据满足n≤10000, m≤200000

保证所有Destroy指令将摧毁的是一条存在的通道

LCT模板题，借此复习一波LCT~

一、基础概念

首先假设我已经会了树剖和splay，嗯好，接下来开始LCT基础操作的复习

LCT与树剖类似，将一棵树剖分成若干树链，然后对于每颗树链，我们用splay维护（同树剖，往往用一颗大的splay存储所有splay的信息），对于每一颗splay，它的节点满足：deep(Lson)

由于有多棵splay，我们暂且称原树根节点所在的splay为主splay树。

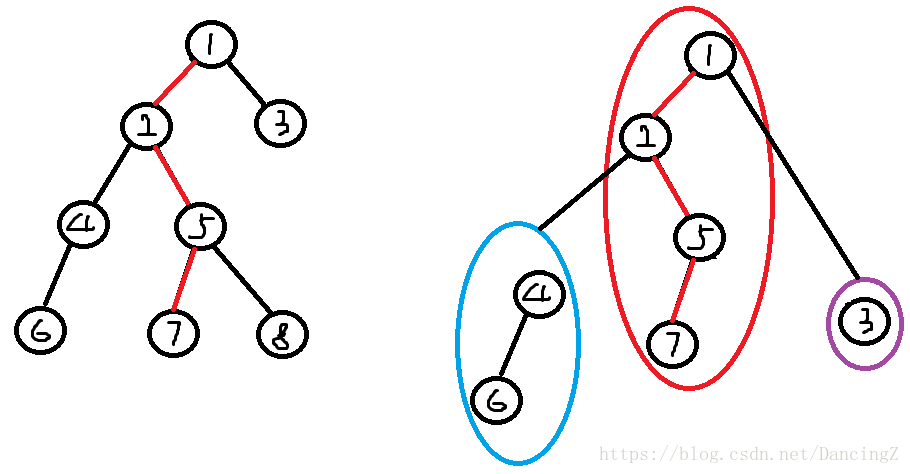
如果我们将树链抽象成一棵棵splay，每一棵splay中，深度最浅的那个节点的父节点，就是这颗splay根节点所存储的父节点，如下图：

因为树链46中，4的深度较浅，所以这颗splay根的父节点就是4的父亲……

二、基本操作

1、Access

access操作，就像splay树的伸展操作一样，有了access操作，我们就可以根据动态树的性质乱搞233

acess(x)表示将x节点到原树的根节点经过的这一条路径变为“重链”，就是说，x->root这条路径上的所有节点被存储在了主splay中。

如何改变呢？我们利用splay存储节点的性质，先将x伸展到根，断开x的右儿子，因为这时右儿子及其子树深度都比x深，然后我们找到x的父亲fx，伸展fx到其对应splay的根，断开fx的右儿子，将x接上去……显然每棵splay的深度总是连续的，我们不会断层，直到操作主splay树完毕后，x以及x->root路径上的点就会存储在主splay中。（电脑绘图太麻烦，有时间就补个模拟图吧）

于是我们就有了如下伪代码：

inline void access(int x){
	int lastx=0;
	while(x){
		splay(x);
		rs(x)=lastx;
		lastx=x;
		x=fa[x];
	}
}

ps:有了access操作后，不需要关注splay的内部操作，我们只需关注每个splay节点间宏观的关系

2、求Lca

inline int access(int x){
	int lastx=0;
	while(x){
		splay(x);
		rs(x)=lastx;
		lastx=x;
		x=fa[x];
	}
	return lastx;
}
inline int lca(int x,int y){
	access(x);
	return access(y);
}

简单提一下，当y的父节点为主splay中的节点时，就出现了重复路径，此时的父节点就是lca（有时间补图）

3、找原树树根

4、改变树根

//将x变为树根
inline void make_root(int x){
	access(x);
	splay(x);
	rev[x]^=1;
}

access(x)之后，x变为深度最深的，我们要将x变为根，即x成为深度最浅的，显然x->root这条路径上的点全部翻转且其余的splay并不会发生改变（区间翻转见文艺平衡树）

5、合并/拆分x，y

inline void link(int x,int y){
	make_root(x);
	p[x]=y;
}
inline void cut(int x,int y){
	make_root(x);
	access(y);
	sp.splay(y);
	sp.p[x]=sp.Ls(y)=0;
}

哈~哈~，基础操作终于巩固完毕，接下来就可以搞这道题了~

#include
using namespace std;
const int N = 2e5+10;
struct Splay{
	bool rev[N];
	int p[N],ch[N][2];
	#define Ls(v) ch[v][0]
	#define rs(v) ch[v][1]
	bool is_root(int x){//splay存储每条树链 
		return (Ls(p[x])^x)&&(rs(p[x])^x);
	}
	inline void pushdown(int x){
		if(rev[x]){
			rev[Ls(x)]^=1,rev[rs(x)]^=1;
			swap(Ls(x),rs(x));
			rev[x]=0;
		}
	}
	inline void rot(int x){
		int f=p[x],gf=p[f],type=rs(f)==x,son=ch[x][!type];
		if(!is_root(f))ch[gf][rs(gf)==f]=x;p[x]=gf;
		ch[p[son]=f][type]=son;
		ch[p[f]=x][!type]=f;//注意要判f是否为根，所以p[f]要后改 
	}
	int top,stk[N];
	inline void splay(int x){
		stk[++top]=x;
		if(!is_root(x))for(int i=x;!is_root(i);i=p[i])stk[++top]=p[i];
		while(top)pushdown(stk[top--]);//采用文艺平衡树中的另一种写法亦可，不过记得最开始要pushdown 
		while(!is_root(x)){
			if(is_root(p[x]))return rot(x),void();
			if((rs(p[p[x]])==p[x])==(rs(p[x])==x))rot(p[x]);
			rot(x);
		}
	}
};
struct LCT{
	Splay sp;
	inline void access(int x){
		int lastx=0;
		while(x){
			sp.splay(x);
			sp.rs(x)=lastx;
			lastx=x;
			x=sp.p[x];
		}
	}
	inline void make_root(int x){
		access(x);
		sp.splay(x);
		sp.rev[x]^=1;
	}
	inline void Link_root(int rt1,int rt2){
		make_root(rt1),sp.p[rt1]=rt2;
	}
	inline void cut_edge(int rt1,int rt2){
		make_root(rt1);
		access(rt2);
		sp.splay(rt2);
		sp.p[rt1]=sp.Ls(rt2)=0;
	}
	inline int FindTRT(int x){
		access(x),sp.splay(x);
		while(sp.Ls(x))x=sp.Ls(x);
		return x;
	}
}lct;
int n,m;
int main(){
	scanf("%d%d",&n,&m);
	char q[10];int x,y;
	while(m--){
		scanf("%s%d%d",q,&x,&y);
		if(q[0]=='Q')cout<<(lct.FindTRT(x)==lct.FindTRT(y)?"Yes":"No")<<"\n";
		if(q[0]=='C')lct.Link_root(x,y);
		if(q[0]=='D')lct.cut_edge(x,y);
	}
	return 0;
}

Ps：其实这道题是要我们维护可删除的并查集，不知道线段树分治能不能做，嗯？