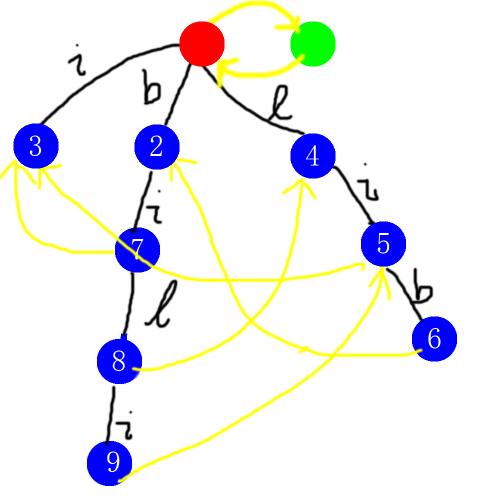
回文自动机 笔记

今天日常给同学@CollinGao 写奥♂义。讲到了这个东西，还是挺有用的，就是有点毒瘤？仿佛没什么人知道的亚子。。。

不是很难理解的算法，我在期中考试考场上就直接yy出了一个来。虽然马上CSP了，但是我还是准备来颓废，写写这篇奥♂义。

基础题型

给你一个字符串，对于每个前缀，求该前缀中有多少前缀不同的回文子串。定义一个回文子串的权值为：长度乘以出现次数。对于每个前缀，也请你求出最大的回文子串的权值是多少。

回文自动机（又名回文树）是干啥的

大家都知道TRIE树（知道即珂，但是如果连听说都没听说过，那劝退了）。在TRIE树上，每个节点表示一个字符串，字符记录在边权上。连一条边表示在这个字符串后面加上一个字符。

那么，回文自动机是怎么弄的的？连一条边，表示在这个字符串前后各加上一个字符。比如某个父亲的字符串为"aba"，连了一条权值为’c’的边到儿子，儿子的字符串就是"cabac"。

然后要注意一点，回文自动机有两个根。其原因很显然，因为一个父亲以下的字符串长度的奇偶性不会改变。所以，两个根分别记录奇数长度和偶数长度的回文串，名字就叫奇根和偶根。偶根很好理解，表示一个空串，其长度为$0$。那么，奇根怎么办呢？仔细一推，单个字符长度为$1$，其父亲的长度为其长度$-2$，也就是说，奇根表示的字符串长度为$-1$？！

没事，$-1$就$-1$，只不过是为了方便计算罢了。实际实现中，考虑到空间问题，我们并不会实际记录表示的字符串，只是记录一个长度$len$。那么，只要让这个点的$len=-1$即珂，一点问题都没有。

fail指针

精髓（准确来讲，是每个自动机的精髓）。对于一个节点，它的$fail$指针是指：除了自己之外，LPS（Longest Palindrome Suffix，最长回文后缀）所对应的点。
如果你仔细咀嚼了这句话，那么你会想这样一个问题：除了自己之外的最长回文子串一定在树上能找到吗？

证明fail一定在树上能找到

（如果您能自己证明，请跳过这段）
设当前节点表示字符串$s$，$fail$指向的节点所对应为$f$，$f^t$表示把$f$反过来，$|f|$表示$f$的长度，如图所示。

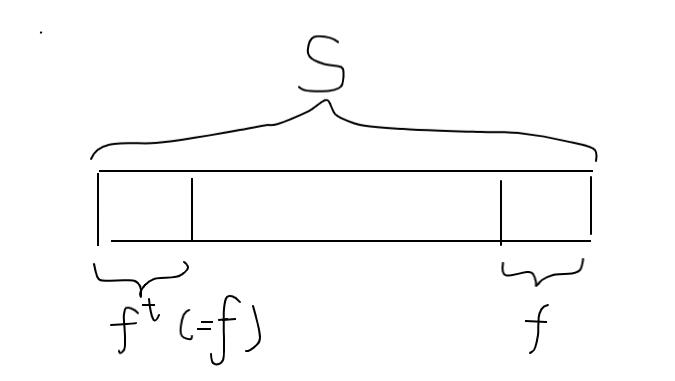
由于$S$是回文串（根据定义），$S$的前缀$|f|$个字符串和后缀$|f|$。$S$和$f$都是回文的，非常容易证明，$S$的$|f|$个前缀和这么长的后缀是一样的。
那么，$f$在后面出现一遍，就说明在前面也出现了一遍。由于我们是从前往后加入到树上的，所以这个串一定能找到。

证毕 $■$

如何构建

上面讲了一下，我们是按照从前往后的顺序插入$s$的每个字符的。对于插入第$i$个位置，我们的任务是找到其$LPS$，并把它插入到树上的正确位置。那么，如何找到呢？

等价一下，这个节点满足：

1. 它是i-1位置的一个回文后缀
2. 它左右字符相等，都是$s[i]$

对于满足条件1，我们记录一个$last$，表示$i-1$插入在了树上哪个位置。（当我们插入完$i$的位置的时候，我们令它为我们找到的位置，即珂维护）

然后$last$显然就是$i-1$的一个回文后缀。但是我们要找到所有的回文后缀，那没问题，我们不断的跳$fail$即珂。

然后还要满足条件2。设现在我们跳到了点$cur$，这个点上的长度值为$len(cur)$。只要判断$s[i]==s[i-len(cur)-1]$即珂。如果满足就退出，不满足就$cur=fail(cur)$，继续循环。

关于$fail$的维护：很简单，和上面找到父亲的过程只差一个$cur$初始值的区别。因为$fail$指针要满足不等于自己，所以，$cur$的初始值，不是$father$，而是$fail(father)$。和找到父亲的步骤还有一点点不同，就是最后找到一个$cur$满足$s[i]==s[i-len(cur)-1]$的时候，返回的不是$cur$而是$cur$的边权为$s[i]$的儿子。这里还有一个至关重要的细节要注意，先求出fail指针，才能连边。代码中会提到。

那么我们来举一个例子。我们要构建的字符串s=“bilibili”。

初始化，构建奇根和偶根。红色是奇根，绿色是偶根。特殊地（忘了讲了），奇根和偶根的$fail$指针（黄色）互相指向对方。

第一步，插入位置$1$。默认是插入到$0$上，失败了再跳$fail$。我们发现，$s[1]!=s[1-len(0)-1]$，于是跳了$fail(0)=1$，然后显然满足了。我们还发现，此时还没有节点，便新建一个节点（编号为$2$），把它接在奇根（$1$）下面。跳一下$fail$，发现$fail$是$0$（显然）。由于很多节点的$fail$都是$0$，这些边我就不连了（为了看起来美观）。效果图：

时间关系，我们不仔细看每一个位置的插入过程，直接跳到第$5$个位置的插入。这之前的图建出来长这样：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UCWACXGt-1574515415064)(https://i.loli.net/2019/11/13/amheuLwg48GFzDc.jpg)]

然后我们大喊一声：King Crimson！

第五步，插入位置$5$，此时前缀为$bilib$。默认插入在$last$上，也就是编号$5$的位置。我们一下就满足了条件，所以我们的确要接在$last$下面。求一下$fail$指针，先到$fail(5)=3$试一下，发现，不行。然后跳到$fail(3)=0$试一下，还不行，跳到$fail(0)=1$再试一下，行了，返回$1$的边权为$s[i]({=}^{\prime }{b}^{\prime })$的儿子，也就是编号为$2$的节点。完成之后，图长这样：

让我们再大喊一声：King Crimson!

最终完成图：

然后我们这就构建好了一个回文自动机。

附：
“我的讲义，能抄下来么？”
“能抄一点。”
“让我康康！”
“你看，这个fail边，应该连在儿子这里的。尽管你这样画很好看，但这个fail边就是这样连的，你不能改变它”
我心里还是有点不服气。图还是我画的好，至于这条边到底连在哪里，我自然是知道的。

—— 选自 鲁迅《藤野先生》

实现（你们最想要的

class Palindrome_Tree //我喜欢写面向对象
{
public:
    char s[N];
    struct node
    {
        int len,fail;
        int ch[26];
    }t[N];//保存一个节点
    node& operator[](int id){return *(t+id);}
    int last;
    int cnt=1;//上一次插入在哪
    void Init(char ss[N])
    {
        FK(t);
        strcpy(s+1,ss+1);
        t[0].len=0;t[0].fail=1;
        t[1].len=-1;t[1].fail=0;//len=-1!!!!!
        //注意:fail是互相指的
        last=0;//开始默认接在0上,后来就接在last上,不行就跳fail
    }

    int Getfail(int fa,int pos)
    {
        int cur=t[fa].fail;
        for(;s[pos]!=s[pos-t[cur].len-1];cur=t[cur].fail); //不行就跳fail

        int id=s[pos]-'a';return t[cur].ch[id];//返回fail的儿子，记住藤野先生的话
    }
    void Insert(int pos)
    {
        // printf("Insert %d\n",pos);
        // 方便理解用

        int cur=last;//注意初始值
        while(s[pos-t[cur].len-1]!=s[pos])
        {
            cur=t[cur].fail;
        }//同上，不行就跳fail的过程

        int id=s[pos]-'a';//当前字符
        if (t[cur].ch[id]==0) //如果还不存在这个节点
        {
            ++cnt;//新加一个节点
            t[cnt].len=t[cur].len+2;//len+=2，显然
            t[cnt].fail=Getfail(cur,pos);//求出fail
            t[cur].ch[id]=cnt;//次序关键！先求fail，再连边
            
            // printf("fail[pos]=%d\n",t[cnt].fail);
        }
        last=t[cur].ch[id];
    }
}T;

应用

我们讲了这么多，来解决些实际问题。

1. 本质不同的回文串个数
   每个点（除了奇根和偶根）都一一对应一个本质不同的回文串。只要输出$cnt-1$即珂。（应该是点数-2，但是由于我是从0开始算点的，所以-1才是正确的）

2. 每个回文串的个数
   每个点维护一个值$cnt$（重名了，但是因为命名空间不一样，写在struct里，所以不会报错）。然后插入一个点时，找到它所在的树上位置，该点上$cnt++$。最后再$cnt[fail(i)]+=cnt[i]$，i从$n$到$1$。和$KMP$中计算每个前缀出现的次数是类似的原理。

尝试一下：

1. 洛谷 板子 （5496）
2. 洛谷 5555
3. bzoj 3676
4. 终于不是板子的：CF17E