Dijkstra算法解题报告——"大一水手"
最短路径-Dijkstra算法解题报告(大一)
算法描述(学于清华出版社《数据结构教程与题解》):
在有向网络中,从某点出发,到达其他任何一点都可能有多条路径,其中必有一条是最短路径(若没有路径,则假设路径是长度为无限大的虚拟路径)。设图共有n个顶点,于是从某一点出发到其他各点的最短路径有n-1条。这n-1条最短路径之间也存在大小关系。
Dijkstra算法就是按照长度递增的次序生成各顶点的最短路径,即先求出长度最小的一条最短路径,然后求出长度第二小的最短路径,etc,最后求出长度最大的最短路径。算法的基本思想是,设置并逐渐扩充一个集合S,S用来存放已求出其最短路径的顶点,则上位确定最短路径的顶点集合是V-S。为称呼方便,以下把源点v到终点w的最短路径简称为顶点w的最短路径,集合S中的顶点称为已求点,集合V-S的顶点称为待求点。算法开始时,S中已求点就是源点自己,以后每一步就是按照最短路径长度递增的顺序在待求点集合中选一个最短路的点来扩充S集合,直到所有顶点都成为已求点。
每一个顶点i都有一个到原点v0的距离值,用数组D[ i]来存放。
已求点的距离值就是该点的最短路径长度,而待求点的距离值则不一定是该点的最短路径长度,因为从原点开始到该待求点可能存在经过其他待求点的最短路径。可以证明的是,若当前待求点中距离值最小的点为v,则其距离值D[v]就是v点的最短路径长度,并且k也是待求点中最短的顶点。
证明如下:
(1) 任取一条从原点v0到u点的路径Pvu,则该路径可能经过若干待求点,设经过的第一个待求点为x,则该路径可分为两段Pvx和Pxu,于是:
Pvu>=Pvx
>=x距离值(因为Pvx中间只经过已求点,而距离值已经是这类路径中最短的)
>=u距离值(因为u点是所有待求点中距离值最小的)
综上所述,u点的距离值就是k的最短路径长度
(2)对任意一个待求点j,任取一条从原点v0到顶点j的路径Pvj,该路径也可能经过若干待求点,设经过的第一个待求点为y,则该路径可分为两段Pvy和Pyj,于是与(1)类似,有Pvj长度>=Pvy长度
>=y距离值
>=u距离值
即u点的距离值也是所有待求点中路径长度最短的。
后面就是对剩余待求点的距离值的调整,因为一旦有u点加入S,剩下的点的距离值有可能减小。
简述:
在做这道题的时候,一开始毫无头绪,有一些思路但不知道从哪里开始实现,于是利用Google查找相关资料,一开始看网上的代码感觉云里雾绕的,就算有注释也不理解,然后查阅了《数据结构教程与题解》这本书的6.6.1单元最短路径内容 之后,才开始了解整段代码,于是照着自己的思路和理解,将百度百科上“破碎的”的代码进行优化和整改,最后实现了更多的功能,也是在不断学习中强化自我和进步。
测试数据:
顶点数n=6
#define Max 1000000
| N=6 |
0 |
1 |
2 |
3 |
4 |
5 |
| 0 |
Max |
Max |
10 |
Max |
30 |
100 |
| 1 |
Max |
Max |
5 |
Max |
Max |
Max |
| 2 |
Max |
Max |
Max |
50 |
Max |
Max |
| 3 |
Max |
Max |
Max |
Max |
Max |
10 |
| 4 |
Max |
Max |
Max |
20 |
Max |
60 |
| 5 |
Max |
Max |
Max |
Max |
Max |
Max |
| 出度点 |
入度点 |
Value |
| 0 |
2 |
10 |
| 0 |
4 |
30 |
| 0 |
5 |
100 |
| 1 |
2 |
5 |
| 2 |
3 |
50 |
| 3 |
5 |
10 |
| 4 |
3 |
20 |
| 4 |
5 |
60 |
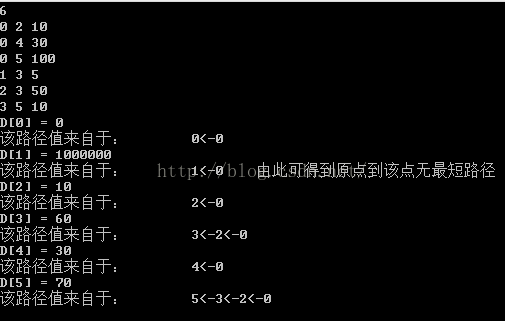
答案:
算法代码:
#include
#define MAX 1000000
using namespace std;
int map[10][10];//邻接矩阵
int D[10];//保存最短路径长度
int final[10];//若final[i] = 1则说明 顶点vi已在集合S中
int node_path[10];//用来存当前节点的前一节点是哪一个
int n = 0;//顶点个数
int v0 = 0;//源点
int v, w;
void ShortestPath_Dijkstra()
{
for (v = 0; v < n; v++) //循环 初始化
{
final[v] = 0;
D[v] = map[v0][v];
node_path[v] = v0;
}
D[v0] = 0;
final[v0] = 0; //初始化 v0顶点属于集合S
//开始主循环 每次求得v0到某个顶点v的最短路径 并加v到集合S中
for (int i = 1; i < n; i++)
{
int min = MAX;
for (w = 0; w < n; w++)
{
//我认为的核心过程--选点
if (!final[w]) //如果w顶点在V-S中,即不在S中
{
//这个过程最终选出的点 应该是选出当前V-S中与S有关联边
//且权值最小的顶点 书上描述为 当前离V0最近的点
if (D[w] < min) { v = w; min = D[w]; }
}
}
if (min == MAX) //如果剩余点的距离都为MAX,则不必再更新距离值
{
break;
}
final[v] = 1; //选出该点后加入到合集S中
for (w = 0; w < n; w++)//更新当前最短路径和距离
{
/*在此循环中 v为当前刚选入集合S中的点
则以点V为中间点 考察 d0v+dvw 是否小于 D[w] 如果小于 则更新
比如加进点 3 则若要考察 D[5] 是否要更新 就 判断 d(v0-v3) + d(v3-v5) 的和是否小于D[5]
*/
if (!final[w] && (min + map[v][w] { D[w] = min + map[v][w]; node_path[w] = v; } } } } int main() { cin >> n; int x, y, weight; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { map[i][j]=MAX; } } for (int j = 0; j < n; j++) { cin >> x >> y >>weight; map[x][y] = weight; } ShortestPath_Dijkstra(); for (int i = 0; i < n; i++) { cout << "D[" << i << "]" << " = " << D[i] << endl; int node=i; cout << "该路径值来自于:" << '\t'< do{ node = node_path[node]; cout << "<-" << node; } while (node != v0); if (D[i] == MAX) { cout << '\t'<<"由此可得到原点到该点无最短路径"; } cout << endl; } return 0; }