课程>
我的课程>
百度架构师手把手教深度学习>
1-2 用Python编写【房价预测】模型>
paddle初级教程第一章 第二节
 王然(学生)
王然(学生)
Notebook
教育
初级
深度学习
Python3
2019-12-19 17:00:50
使用Numpy构建神经网络
本节将使用Python语言和Numpy库来构建神经网络模型,向读者展示神经网络的基本概念和工作过程。
构建神经网络/深度学习模型的基本步骤
如之前的介绍,应用于不同场景的深度学习模型具备一定的通用性,均可以从下述五个步骤来完成模型的构建和训练。
- 数据处理:从本地文件或网络地址读取数据,并做预处理操作,如校验数据的正确性等。
- 模型设计:完成网络结构的设计(模型要素1),相当于模型的假设空间,即模型能够表达的关系集合。
- 训练配置:设定模型采用的寻解算法(模型要素2),即优化器,并指定计算资源。
- 训练过程:循环调用训练过程,每轮均包括前向计算 、损失函数(优化目标,模型要素3)和后向传播这三个步骤。
- 保存模型:将训练好的模型保存,以备预测时调用。
下面使用Python编写预测波士顿房价的模型,一样遵循这样的五个步骤。 正是由于这个建模和训练的过程存在通用性,即不同的模型仅仅在模型三要素上不同,而五个步骤中的其它部分保持一致,深度学习框架才有用武之地。
波士顿房价预测
波士顿房价预测是一个经典的机器学习问题,类似于程序员世界的“Hello World”。波士顿地区的房价是由诸多因素影响的,该数据集统计了13种可能影响房价的因素和该类型房屋的均价,期望构建一个基于13个因素预测房价的模型。预测问题根据预测输出的类型是连续的实数值,还是离散的标签,区分为回归任务和分类任务。因为房价是一个连续值,所以房价预测显然是一个回归任务。下面我们尝试用最简单的线性回归模型解决这个问题,并用神经网络来实现这个模型。
线性回归模型
假设房价和各影响因素之间能够用线性关系来描述(类似牛顿第二定律的案例):
y=∑j=1Mxjwj+by = {\sum_{j=1}^Mx_j w_j} + b y=j=1∑Mxjwj+b
模型的求解即是通过数据拟合出每个wjw_jwj和bbb。wjw_jwj和bbb分别表示该线性模型的权重和偏置。一维情况下,wjw_jwj和bbb就是直线的斜率和截距。
数据处理
在搭建模型之前,让我们先导入数据,查阅下内容。房价数据存放在本地目录下的housing.data文件中,通过执行如下的代码可以导入数据并查阅。
import numpy as np
import json
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
data
array([6.320e-03, 1.800e+01, 2.310e+00, ..., 3.969e+02, 7.880e+00,
1.190e+01])
因为读入的原始数据是1维的,所有数据都连在了一起。所以将数据的形状进行变换,形成一个2维的矩阵。每行为一个数据样本(14个值),每个数据样本包含13个X(影响房价的特征)和一个Y(该类型房屋的均价)。
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS',
'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
data = data.reshape([data.shape[0] // feature_num, feature_num])
print(len(feature_names))
print(data.shape[0])
print(data.shape[0] // feature_num)
x = data[0]
print(x.shape)
print(x)
(14,)
[6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+01
4.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00 2.400e+01]
取80%的数据作为训练集,预留20%的数据用于测试模型的预测效果(训练好的模型预测值与实际房价的差距)。打印训练集的形状可见,我们共有404个样本,每个样本含有13个特征和1个预测值。
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
training_data.shape
对每个特征进行归一化处理,使得每个特征的取值缩放到0~1之间。这样做有两个好处:
- 模型训练更高效。
- 特征前的权重大小可代表该变量对预测结果的贡献度(因为每个特征值本身的范围相同)。
maximums, minimums, avgs = \
training_data.max(axis=0), \
training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
print(maximums)
print(minimums)
for i in range(feature_num):
data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
[0.97853679 0.85767327 0.64103506 0.91336634 0.69808245 0.4688429
0.36634938 0.72313892 0.74827809 0.65363071 0.42274068 0.0519112
0.73441086 0.57387239]
[-0.02146321 -0.14232673 -0.35896494 -0.08663366 -0.30191755 -0.5311571
-0.63365062 -0.27686108 -0.25172191 -0.34636929 -0.57725932 -0.9480888
-0.26558914 -0.42612761]
[-1.23663456e-18 5.45493244e-17 -1.09923072e-18 -5.13890360e-17
1.67632684e-17 -4.12211519e-19 -3.02288447e-18 -3.09158639e-18
-3.02288447e-17 2.19846143e-18 -2.74807679e-18 1.68319704e-18
-3.29769215e-18 4.25951903e-18]
将上述几个数据处理操作合并成load data函数,并确认函数的执行效果。
def load_data():
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
data = data.reshape([data.shape[0] // feature_num, feature_num])
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
for i in range(feature_num):
data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:]
print(x[0])
print(y[0])
[-0.02146321 0.03767327 -0.28552309 -0.08663366 0.01289726 0.04634817
0.00795597 -0.00765794 -0.25172191 -0.11881188 -0.29002528 0.0519112
-0.17590923]
[-0.00390539]
如果将输入特征和输出预测值均以向量表示,输入特征x一共有13个分量,y只有1个分量,所以参数权重的形状(shape)应该是13×113\times113×1。假设我们以如下任意数字赋值参数做初始化:
w=[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,−0.1,−0.2,−0.3,−0.4,0.0]w=[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3,-0.4, 0.0]w=[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,−0.1,−0.2,−0.3,−0.4,0.0]
w = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3, -0.4, 0.0]
w = np.array(w).reshape([13, 1])
取出第1条样本数据,观察样本的特征向量与参数向量相乘之后的结果。
x1=x[0]
t = np.dot(x1, w)
print(t)
此外,完整的线性回归公式,还需要初始化偏移量bbb,同样随意赋初值-0.2。 那么,线性回归模型的完整输出是z=t+bz=t+bz=t+b,这个从特征和参数计算输出值的过程称为“前向计算”。
b = -0.2
z = t + b
print(z)
构建神经网络
将上述计算预测输出的过程以“类和对象”的方式来描述,实现的方案如下所示。类成员变量有参数 w 和 b,并写了一个forward函数(代表“前向计算”)完成上述从特征和参数到输出预测值的计算过程。
class Network(object):
def __init__(self, num_of_weights):
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
基于Network类的定义,模型的计算过程可以按下述方式达成。
net = Network(13)
x1 = x[0]
y1 = y[0]
z = net.forward(x1)
print(z)
通过模型计算x1x_1x1表示的影响因素所对应的房价应该是zzz, 但实际数据告诉我们房价是yyy,这时我们需要有某种指标来衡量预测值zzz跟真实值yyy之间的差距。对于回归问题,最常采用的衡量方法是使用均方误差作为评价模型好坏的指标,具体定义如下:
Loss=(y−z)2Loss = (y - z)^2 Loss=(y−z)2
上式中的LossLossLoss(简记为: LLL) 通常也被称作损失函数,它是衡量模型好坏的指标,在回归问题中均方误差是一种比较常见的形式,分类问题中通常会采用交叉熵损失函数,在后续的章节中会更详细的介绍。 对一个样本计算损失的代码实现如下:
Loss = (y1 - z)*(y1 - z)
print(Loss)
因为计算损失时需要把每个样本的损失都考虑到,所以我们需要对单个样本的损失函数进行求和,并除以样本总数NNN。
L=1N∑i(y(i)−z(i))2L= \frac{1}{N}\sum_i{(y^{(i)} - z^{(i)})^2} L=N1i∑(y(i)−z(i))2
对上面的计算代码做出相应的调整,在Network类下面添加损失函数的计算过程如下
class Network(object):
def __init__(self, num_of_weights):
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
使用上面定义的Network类,可以方便的计算预测值和损失函数。
需要注意,类中的变量x, w,b, z, error等均是向量。以变量x为例,共有两个维度,一个代表特征数量(=13),一个代表样本数量(演示程序如下)。
net = Network(13)
x1 = x[0:3]
y1 = y[0:3]
z = net.forward(x1)
print('predict: ', z)
loss = net.loss(z, y1)
print('loss:', loss)
predict: [[-0.63182506]
[-0.55793096]
[-1.00062009]]
loss: 0.7229825055441156
神经网络的训练
上述计算过程描述了如何构建神经网络,通过神经网络完成预测值和损失函数的计算。接下来将介绍如何求解参数www和bbb的数值,这个过程也称为模型训练。模型训练的目标是让定义的损失函数尽可能的小,也就是说找到一个参数解www和bbb使得损失函数取得极小值。
求解损失函数的极小值
基于最基本的微积分知识,函数在极值点处的导数为0。那么,让损失函数取极小值的www和bbb应该是下述方程组的解:
∂L∂wj=0, for j=0,...,12\frac{\partial{L}}{\partial{w_j}}=0, \ \ for \ \ \ j = 0, ..., 12 ∂wj∂L=0, for j=0,...,12
∂L∂b=0\frac{\partial{L}}{\partial{b}}=0 ∂b∂L=0
将样本数据(x,y)(x, y)(x,y)带入上面的方程组固然可以求解出www和bbb的值,但是这种方法只对线性回归这样简单的情况有效。如果模型中含有非线性变换,或者损失函数不是均方差这种简单形式,则很难通过上式求解。为了避免这一情况,下面我们将引入更加普适的数值求解方法。
梯度下降法
训练的关键是找到一组(w,b)(w, b)(w,b)使得损失函数LLL取极小值。我们先看一下损失函数LLL只随两个参数变化时的简单情形,启发下寻解的思路。
L=L(w5,w9)L=L(w_5, w_9) L=L(w5,w9)
这里我们将w0,w1,...,w12w_0, w_1, ..., w_{12}w0,w1,...,w12中除w5,w9w_5, w_9w5,w9之外的参数和bbb都固定下来,可以用图画出L(w5,w9)L(w_5, w_9)L(w5,w9)的形式。
net = Network(13)
losses = []
w5 = np.arange(-160.0, 160.0, 1.0)
w9 = np.arange(-160.0, 160.0, 1.0)
losses = np.zeros([len(w5), len(w9)])
for i in range(len(w5)):
for j in range(len(w9)):
net.w[5] = w5[i]
net.w[9] = w9[j]
z = net.forward(x)
loss = net.loss(z, y)
losses[i, j] = loss
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
w5, w9 = np.meshgrid(w5, w9)
ax.plot_surface(w5, w9, losses, rstride=1, cstride=1, cmap=‘rainbow’)
plt.show()
简单情形——只考虑两个参数w5w_5w5和w9w_9w9
对于这种简单情形,我们利用上面的程序在3维空间中画出了损失函数随参数变化的曲面图,从上图可以看出有些区域的函数值明显比周围的点小。需要说明的是:为什么这里我们选择w5w_5w5和w9w_9w9来画图?这是因为选择这两个参数的时候,可比较直观的从损失函数的曲面图上发现极值点的存在。其他参数组合,从图形上观测损失函数的极值点不够直观。
上文提到,直接求解导数方程的方式在多数情况下较困难,本质原因是导数方程往往正向求解容易(已知X,求得Y),反向求解较难(已知Y,求得X)。这种特性的方程在很多加密算法中较为常见,与日常见到的锁头特性一样:已知“钥匙”,锁头判断是否正确容易;已知“锁头”,反推钥匙的形状比较难。
这种情况特别类似于一位想从山峰走到坡谷的盲人,他看不见坡谷在哪(无法逆向求解出Loss导数为0时的参数值),但可以伸脚探索身边的坡度(当前点的导数值,也称为梯度)。那么,求解Loss函数最小值可以“从当前的参数取值,一步步的按照下坡的方向下降,直到走到最低点”实现。这种方法个人称它为“瞎子下坡法”。哦不,有个更正式的说法“梯度下降法”。
现在我们要找出一组[w5,w9][w_5, w_9][w5,w9]的值,使得损失函数最小,实现梯度下降法的方案如下:
- 随机的选一组初始值,例如: [w5,w9]=[−100.0,−100.0][w_5, w_9] = [-100.0, -100.0][w5,w9]=[−100.0,−100.0]
- 选取下一个点[w5′,w9′][w_5^{'} , w_9^{'}][w5′,w9′]使得 L(w5′,w9′)L(w5′,w9′)<L(w5,w9)
- 重复上面的步骤2,直到损失函数几乎不再下降
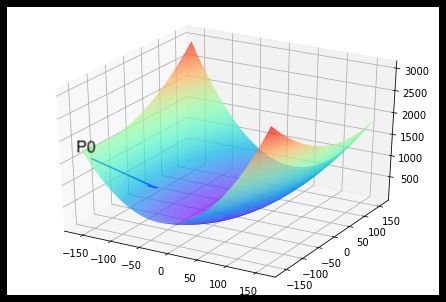
图1-2-1 :梯度下降方向示意图
如何选择[w5′,w9′][w_5^{'} , w_9^{'}][w5′,w9′]是至关重要的,第一要保证LLL是下降的,第二要使得下降的趋势尽可能的快。微积分的基础知识告诉我们,沿着梯度的反方向,是函数值下降最快的方向,如下图所示在点P0P_0P0,[w5,w9]=[−100.0,−100.0][w_5, w_9] = [-100.0, -100.0][w5,w9]=[−100.0,−100.0],梯度方向是图中P0P_0P0点的箭头指向的方向,沿着箭头方向向前移动一小步,可以观察损失函数的变化。 在P0P_0P0点,[w5,w9]=[−150.0,−150.0][w_5, w_9] = [-150.0, -150.0][w5,w9]=[−150.0,−150.0],可以计算出,此时的loss在1300左右。
计算梯度
上面我们讲过了损失函数的计算方法,这里稍微加以改写,引入因子12\frac{1}{2}21,定义损失函数如下
L=12N∑i=1N(y(i)−z(i))2L= \frac{1}{2N}\sum_{i=1}^N{(y^{(i)} - z^{(i)})^2} L=2N1i=1∑N(y(i)−z(i))2
其中ziz_izi是网络对第iii个样本的预测值
z(i)=∑j=012xj(i)w(j)+bz^{(i)} = \sum_{j=0}^{12}{x_j^{(i)} w^{(j)}} + b z(i)=j=0∑12xj(i)w(j)+b
可以计算出LLL对www和bbb的偏导数
∂L∂wj=1N∑iN(z(i)−y(i))∂z(i)wj=1N∑iN(z(i)−y(i))xj(i)\frac{\partial{L}}{\partial{w_j}} = \frac{1}{N}\sum_i^N{(z^{(i)} - y^{(i)})\frac{\partial{z^{(i)}}}{w_j}} = \frac{1}{N}\sum_i^N{(z^{(i)} - y^{(i)})x_j^{(i)}} ∂wj∂L=N1i∑N(z(i)−y(i))wj∂z(i)=N1i∑N(z(i)−y(i))xj(i)
∂L∂b=1N∑iN(z(i)−y(i))∂z(i)b=1N∑iN(z(i)−y(i))\frac{\partial{L}}{\partial{b}} = \frac{1}{N}\sum_i^N{(z^{(i)} - y^{(i)})\frac{\partial{z^{(i)}}}{b}} = \frac{1}{N}\sum_i^N{(z^{(i)} - y^{(i)})} ∂b∂L=N1i∑N(z(i)−y(i))b∂z(i)=N1i∑N(z(i)−y(i))
从导数的计算过程可以看出,因子12\frac{1}{2}21被消掉了,这是因为二次函数求导的时候会产生因子222,这也是我们将损失函数改写的原因
这里我们感兴趣的是w5w_5w5和w9w_9w9,
∂C∂w5=1N∑iN(z(i)−y(i))x5(i)\frac{\partial{C}}{\partial{w_5}} = \frac{1}{N}\sum_i^N{(z^{(i)} - y^{(i)})x_5^{(i)}} ∂w5∂C=N1i∑N(z(i)−y(i))x5(i)
∂C∂w9=1N∑iN(z(i)−y(i))x9(i)\frac{\partial{C}}{\partial{w_9}} = \frac{1}{N}\sum_i^N{(z^{(i)} - y^{(i)})x_9^{(i)}} ∂w9∂C=N1i<

