JPEG霍夫曼编码教程

转译自：https://www.impulseadventure.com/photo/jpeg-huffman-coding.html

量化后，霍夫曼/熵编码是JPEG压缩文件大小节省的重要因素之一。本页提供了有关霍夫曼编码如何在JPEG图像中工作的教程。如果您想知道JPEG压缩是如何工作的，这可能会为您提供一些详细的见解。

为什么我写这个教程

在试图理解JPEG压缩的内部工作原理时，我无法在网上找到关于如何在JPEG图像压缩环境中使用霍夫曼编码的任何真实细节。有一些描述通用霍夫曼编码方案的manysites，但是没有描述它在JPEG图像中出现的方式，在分析了DRT表，交错的色度子采样组件等之后。虽然相对容易理解JPEG标记提取，但是扫描数据段是图像数据中最不了解和最重要的部分。因此，我决定创建一个页面来完成解压缩示例。希望其他人会觉得这很有用！

JPEG标准中的相关部分非常模糊 - 因此我开始分析几个JPEG图像以反向设计如何在JPEG JFIF文件中应用霍夫曼编码。

最近更新：

[09/22/2009]：更正了表5（DC 00代码的添加条目）。
[2008年9月19日]：更正了表1（长度为9位的代码的添加条目）。
[2007年3月12日]：修正了表5（代码00101）附近文本中的拼写错误。添加了JPEGsnoop输出（在教程结束时）。
[2007年7月27日]：添加了描述如何将DHT扩展为位串的部分。

目标

本教程的目标是获取一个简单的JPEG图像，并尝试手动解码压缩的图像数据，了解霍夫曼压缩方案在此过程中的工作原理。

最简单的JPEG示例

大多数数码照片都是全彩色自然/有机图像，这意味着所有三个图像组件（一个亮度和两个颜色通道）都将具有低频和高频内容。此外，几乎所有数码照片都使用色度子采样，这使得提取过程更加复杂。为了显示基本的霍夫曼提取，我们将从最简单的所有JPEG图像开始：
•灰度 - 两个颜色通道中没有内容
•每个MCU的纯色 - 通过使8x8块中的所有像素具有相同的颜色，将不会有AC组件。
•无色度子采样 - 使扫描数据提取更简单：Y，Cb，Cr，Y，Cb，Cr等
•小图像 - 总图像大小为16x8 =两个MCU或块。这使得本教程中的提取更短。

创建图像

出于本教程的目的，我的工作图像将只是一个16x8像素的图像，有两个纯色块：一个是黑色，另一个是白色。请注意，每个块的大小为8x8像素。实际图片如下：。如果要下载它，请右键单击并选择“将图片另存为...”

创建样本图像非常简单，工作在1600％视图。重要的是，尺寸和内容的任何变化都在8像素边界上。在两个方向上，整体图像尺寸也应该是8像素的倍数。下图是放大版本，网格重叠。
 
创建图像后，使用Photoshop CS2的Save for Web ...命令保存图像。这样可以保留文件大小，因为它会丢弃与本教程无关的其他无关文件信息（元数据等）。其他一些要点：
##使用Save for Web - 将总文件内容减少到最小子集。
##使用质量等级51+ - 根据Photoshop Save for Web操作的方式，这确保了JPEG编码过程中没有色度可以进行二次放大。我用这个例子的质量80。
##转向优化关闭 - 对于此示例的目的，我认为使用逼真的霍夫曼表而不是退化单入口表非常重要。因此，我建议不要使用JPEG霍夫曼表优化。
##其他设置：模糊关闭，逐行关闭，ICC配置文件关闭。

灰度Photoshop图像

应该注意的是，当您从Ph​​otoshop中保存JPEG图像时，它始终包含三个组件（Y，Cb，Cr）。如果将模式更改为灰度（通过模式 - >灰度），即使JPEG标准支持仅包含一个组件的图像（假设为灰度），三个组件仍会保存。

什么是霍夫曼编码/熵编码？

霍夫曼编码是一种采用符号（例如字节，DCT系数等）并用根据统计概率分配的可变长度代码对其进行编码的方法。经常使用的符号将使用仅占用几个比特的代码进行编码，而很少使用的符号由需要更多比特来编码的符号表示。

JPEG文件包含最多4个霍夫曼表，用于定义这些可变长度代码（占用1到16位）和代码值（8位字节）之间的映射。创建这些表通常涉及计算频率

解码JPEG扫描数据

使用JPEGsnoop

对于那些试图理解JPEG图像中复杂霍夫曼解码的人，我很高兴地报告JPEGsnoop现在可以报告每个MCU的所有可变长度代码解码（使用详细解码选项）。对于示例输出，请滚动到本教程的底部。

手工解码

以下是手工完成的解码方法，对于大多数图像来说显然是不切实际的，但这里详细说明是为了帮助人们学习所涉及的过程。
 

上面的十六进制转储数据流显示以黄色标记的扫描开始（SOS标记0xFFDA）的开始，然后是绿色的一些其他详细信息以及以深蓝色选择的实际扫描数据。最后，图像以图像结束（EOI标记0xFFD9）终止。因此，霍夫曼编码的数据内容只有9个字节长。

压缩文件大小的比较

为了比较，原始图像（16像素乘8像素）包含总共128个像素（2个MCU）。每通道8位（RGB），这对应于384字节的未压缩图像大小（128像素×8位/通道×3通道×1字节/ 8位）。显然，使用像GIF这样的游程编码格式会在这样的例子中产生更多的图像压缩（尽管GIF实际上需要22个字节来编码流，因为有16个独立的运行）。 JPEG并非真正设计为针对此类合成（非有机）图像进行优化。

如果使用优化的JPEG编码，则可以进一步减小图像内容的大小。在示例图像中，优化版本具有小得多的霍夫曼表（DHT）和较短的位串以表示相同的码字。净效果是图像内容大小进一步减小（至7个字节）。

File Format	Total Size	Overhead Size	Image Content Size
BMP (Uncompressed)	440 Bytes	56 Bytes	384 Bytes
JPEG	653 Bytes	644 Bytes	9 Bytes
JPEG (Optimized)	304 Bytes	297 Bytes	7 Bytes
GIF	60 Bytes	38 Bytes	22 Bytes

扫描数据解码

扫描数据是：

FC FF 00 E2 AF EF F3 15 7F

为了在数据损坏的情况下提供弹性，JPEG标准允许JPEG标记出现在霍夫曼编码的扫描数据段中。 因此，JPEG解码器必须注意任何标记（如0xFF字节所示，后跟非零字节）。 如果霍夫曼编码方案需要写入0xFF字节，那么它会写入0xFF后跟0x00  - 一个称为添加填充字节的过程。

为了我们的提取目的，我们将替换任何填充字节（0xFF00和0xFF）：

FC FF E2 AF EF F3 15 7F

期望图像内容是3个成分（Y，Cb，Cr）。 在每个组件内，序列始终是一个DC值，后跟63个AC值。

对于没有色度子采样的每个MCU，我们希望编码以下数据：

Section	1	2	3	4	5	6
Component	Y		Cb		Cr
AC / DC	DC	AC	DC	AC	DC	AC

请注意，有些人会将色度通道的顺序混淆，并假设它是YCrCb。

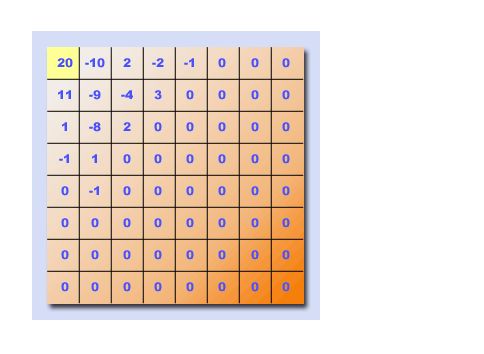
下图显示了数码照片中单个MCU（8x8像素方块）的DCT矩阵通常是什么样子。 这些是量化后的条目，其导致许多较高频率分量（朝向矩阵的右下角）变为零。 通过频域矩阵表示中的值的分布，可以确定8×8像素正方形具有非常小的高频内容（即，它仅具有逐渐的强度/颜色变化）。

DC分量表示8x8 MCU中所有像素的平均值。由于我们故意创建了一个图像，其中8x8块中的所有像素都相同，我们希望该值代表黑色或白色“颜色”。 DC条目（＃0）中提供的代码表示霍夫曼编码的大小（例如1-10位），它是表示MCU平均值所需的位数（例如-511 ... + 511） 。

注意，DC分量被编码为相对于前一个块的DC分量的相对值。假设JPEG图像中的第一个块具有前一个块值为零。

在单个DC组件输入之后，一个或多个条目用于描述MCU中的剩余63个条目。这些条目（1..63）表示DCT变换和量化之后的低频和高频AC系数。较早的条目表示低频内容，而后面的条目表示高频图像内容。由于JPEG压缩算法使用量化来将这些高频值中的许多值减少到零，因此通常在较早的系数中具有多个非零条目并且在矩阵的末尾具有长的零系数。

出于本教程的目的，我故意在两个MCU的每个中创建了一个在所有8x8像素上具有恒定颜色的图像。因为每个8x8像素区域的值没有变化，所以块内没有AC（或更高频率的内容）。结果，AC部分中的所有63个条目预期为零（与上图不同）。这使我们可以专注于DC组件，我们希望从MCU更改为MCU模块。

前面显示的十六进制字符串（删除填充字节后）可以二进制表示如下：

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111

提取霍夫曼代码表

使用JPEGsnoop等实用程序，可以从JPEG图像文件中提取Huffman表。通常，您会发现四个可以填充的条目（用DHT标记标记）：

• DHT Class=0 ID=0 - Used for DC component of Luminance (Y)
• DHT Class=1 ID=0 - Used for AC component of Luminance (Y)
• DHT Class=0 ID=1 - Used for DC component of Chrominance (Cb & Cr)
• DHT Class=1 ID=1 - Used for AC component of Chrominance (Cb & Cr)

霍夫曼压缩表以某种令人困惑的方式编码。虽然您可以手动绘制二叉树，但如果您依赖JPEGsnoop等工具为所有四个DHT部分中的每个霍夫曼代码生成所有二进制比较字符串，则会更容易。

为了本教程的目的，从Photoshop创建的JPEG文件中提取了以下四个表。其他JPEG图像可能依赖于不同的DHT表，因此在分析文件之前提取它们非常重要。请注意，启用JPEG优化将创建截然不同的Huffman表，条目少得多。对于比较点，本教程中描述的图像只需要一个条目的优化霍夫曼表来表示我们的图像内容。

注意：重要的是要意识到在每种情况下，JPEG文件中的DHT条目仅列出长度和代码值，而不是实际的位串映射。您可以重建DHT表的二叉树表示来派生位串！有关详细信息，请参阅本教程末尾附近的DHT扩展部分。

表1 - 霍夫曼 - 亮度（Y） - DC

Length	Bits	Code
3 bits	000 001 010 011 100 101 110	04 05 03 02 06 01 00 (End of Block)
4 bits	1110	07
5 bits	1111 0	08
6 bits	1111 10	09
7 bits	1111 110	0A
8 bits	1111 1110	0B

Table 2 - Huffman - Luminance (Y) - AC

Length	Bits	Code
2 bits	00 01	01 02
3 bits	100	03
4 bits	1010 1011 1100	11 04 00 (End of Block)
5 bits	1101 0 1101 1 1110 0	05 21 12
6 bits	1110 10 1110 11	31 41
...	...	...
12 bits	... 1111 1111 0011 ...	... F0 (ZRL) ...
...	...	...
16 bits	... 1111 1111 1111 1110	... FA

表3 - 霍夫曼 - 色度（Cb和Cr） - DC

Length	Bits	Code
2 bits	00 01	01 00 (End of Block)
3 bits	100 101	02 03
4 bits	1100 1101 1110	04 05 06
5 bits	1111 0	07
6 bits	1111 10	08
7 bits	1111 110	09
8 bits	1111 1110	0A
9 bits	1111 1111 0	0B

表4-霍夫曼 - 色度（Cb和Cr） - AC

Length	Bits	Code
2 bits	00 01	01 00 (End of Block)
3 bits	100 101	02 11
4 bits	1100	03
5 bits	1101 0 1101 1	04 21
6 bits	1110 00 1110 01 1110 10	12 31 41
...	...	...
9 bits	... 1111 1100 0 ...	... F0 (ZRL) ...
...	...	...
16 bits	... 1111 1111 1111 1110	... FA

表5  - 霍夫曼DC值编码

下表显示了如何将DC条目后面的位字段转换为其带符号的十进制等效值。 使用此表，从DC代码值开始，然后在代码后提取“大小”位数。 这些“附加位”将表示已签名的“DC值”，该值成为该块的DC值。 请注意，此表适用于任何JPEG文件 - 此表不会写入JPEG文件本身的任何位置。

例如，让我们假设一个人即将解压缩色度DC条目。 如果先前解码的“DC代码”是05，那么我们必须在代码位之后提取5位。 如果接下来的5位是00101，那么这可以解释为十进制-26。 位10001将是+17,11110将是+30。

DC Code	Size	Additional Bits		DC Value
00	0			0
01	1	0	1	-1	1
02	2	00,01	10,11	-3,-2	2,3
03	3	000,001,010,011	100,101,110,111	-7,-6,-5,-4	4,5,6,7
04	4	0000,...,0111	1000,...,1111	-15,...,-8	8,...,15
05	5	0 0000,...	...,1 1111	-31,...,-16	16,...,31
06	6	00 0000,...	...,11 1111	-63,...,-32	32,...,63
07	7	000 0000,...	...,111 1111	-127,...,-64	64,...,127
08	8	0000 0000,...	...,1111 1111	-255,...,-128	128,...,255
09	9	0 0000 0000,...	...,1 1111 1111	-511,...,-256	256,...,511
0A	10	00 0000 0000,...	...,11 1111 1111	-1023,...,-512	512,...,1023
0B	11	000 0000 0000,...	...,111 1111 1111	-2047,...,-1024	1024,...,2047

第1块 - 亮度

亮度（Y） -  DC

参考Y（DC）表（表1），我们从编码流的前几位开始（1111 1100 1111 ...）并且识别出代码x0A与位串1111 110匹配。

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：0A

该代码暗示随后的十六进制A（10）附加位表示DC分量的有符号值。 该代码之后的下一个十位是0 1111 1111 1.上面的表5示出了由这些“附加位”表示的DC值 - 在这种情况下，位串对应于值-512。

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>值：-512

我们目前的进展：

Bits	1111 1100 1111 1111 1	110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
MCU	1	???
Component	Y	???
AC/DC	DC	???
Value	-512	???

亮度（Y） -  AC

在DC分量之后，我们开始用于Y亮度的63入口AC矩阵。 这使用了不同的霍夫曼表（表2）。

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：00（EOB）

在上述霍夫曼代码表中，代码1100对应于EOB（块结束）。 因此，AC组件提前缩短（没有其他代码）。 这意味着矩阵的所有63个条目（除第一个条目之外的所有条目，即DC分量）都是零。 由于我们已经完成了亮度分量，我们接着转向色度分量（Cb和Cr）。

Bits	1111 1100 1111 1111 1	1100	010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
MCU	1		???
Component	Y		???
AC/DC	DC	AC	???
Value	-512	0	???

第1块 - 色度

色度（Cb） -  DC

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：00（EOB）

色度DC结束，从AC开始。

色度（Cb） -  AC

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：00（EOB）

同样，AC立即终止。 现在，我们继续第二个色度通道Cr。

Bits	1111 1100 1111 1111 1	1100	01	01	010 1111 1110 1111 1111 0011 0001 0101 0111 1111
MCU	1				???
Component	Y		Cb		???
AC/DC	DC	AC	DC	AC	???
Value	-512	0	0	0	???

色度（Cr） -  DC

有关霍夫曼代码，请参阅表3。

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：00（EOB）

这标志着DC的终结。

色度（Cr） -  AC

有关霍夫曼码，请参阅表4。

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：00（EOB）

这标志着AC的终结。

Bits	1111 1100 1111 1111 1	1100	01	01	01	01	111 1110 1111 1111 0011 0001 0101 0111 1111
MCU	1						???
Component	Y		Cb		Cr		???
AC / DC	DC	AC	DC	AC	DC	AC	???
Value	-512	0	0	0	0	0	???

第2块 - 亮度

亮度（Y） -  DC

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：0A

此代码表示该值存储在接下来的十位中（十六进制中的A为十进制10）：

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>值：+1020

Bits	1111 1100 1111 1111 1	1100	01	01	01	01	111 1110 1111 1111 00	11 0001 0101 0111 1111
MCU	1						2	???
Component	Y		Cb		Cr		Y	???
AC / DC	DC	AC	DC	AC	DC	AC	DC	???
Value	-512	0	0	0	0	0	+1020	???

亮度（Y） -  AC

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：EOB

块结束指示符表示所有剩余值均为零。 由于我们甚至没有使用第一个值，所有63个值都可以解释为零。 这意味着没有非DC图像内容，这是预期的，因为块中的所有64个像素（8x8）是相同的颜色。

Bits	1111 1100 1111 1111 1	1100	01	01	01	01	111 1110 1111 1111 00	1100	01 0101 0111 1111
MCU	1						2		???
Component	Y		Cb		Cr		Y		???
AC / DC	DC	AC	DC	AC	DC	AC	DC	AC	???
Value	-512	0	0	0	0	0	+1020	0	???

第2块 - 色度

色度（Cb） -  DC

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：00（EOB）

色度（Cb） -  AC

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：00（EOB）

色度（Cr） -  DC

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：00（EOB）

色度（Cr） -  AC

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111
=>代码：00（EOB）

Bits	1111 1100 1111 1111 1	1100	01	01	01	01	111 1110 1111 1111 00	1100	01	01	01	01	11 1111
MCU	1						2						X
Component	Y		Cb		Cr		Y		Cb		Cr		X
AC / DC	DC	AC	DC	AC	DC	AC	DC	AC	DC	AC	DC	AC	X
Value	-512	0	0	0	0	0	+1020	0	0	0	0	0	X

剩余

因为扫描数据必须以字节边界结束，所以可能存在仅仅被抛出的剩余的比特。在这种情况下，我们看到将被丢弃的6位（全-1）。

1111 1100 1111 1111 1110 0010 1010 1111 1110 1111 1111 0011 0001 0101 0111 1111

转换为空间域

现在我们有了DCT（离散余弦变换）值，我们可以尝试确定图像内容在空间域中的含义。记住我们从霍夫曼编码解压缩的DC和AC值是图像的频域表示，而不是真实的YCbCr值。

假设Cb和Cr通道中的所有值（色度）都为零，我们可以假设图像是灰度级的，并且不稳定地关注亮度值（亮度）。

其次，所有AC分量值都为零，这意味着图像中没有更高频率的内容 - 事实上，我们可以确定每个8x8块中的所有图像数据具有相同的颜色和强度（即只剩下直流分量）。

我们可以确定以下内容：

Block	Encoded (Relative) DC Value
1	Y = -512
2	Y = +1020

相对直流到绝对直流

注意，DC分量被编码为与前一个块的差异（假设第一个块相对于零开始）。 因此，我们知道块1的DC值为-512，但块2相对于块1具有+1020的DC值。因此，我们现在知道：

 

Block	Actual (Absolute) DC Value
1	Y = -512
2	Y = +508

DCT到RGB

最后，我们要将DCT DC值转换为RGB值。 假设DCT变换的增益为4，我们将值除以4得到block1 = -128，block2 = +127。

现在，我们必须在YCbCr和RGB之间进行转换。 请参阅JPEG颜色转换页面上提供的公式。 在那里，您将看到我们需要+128的电平转换才能获得范围内的输入值（0..255）。

颜色转换产生RGB值：

Block	RGB Value (hex)	RGB Value (decimal)
1	(0x00,0x00,0x00)	(0,0,0)
2	(0xFF,0xFF,0xFF)	(255,255,255)

...这些是用于创建JPEG图像的原始值！

将DHT表扩展为二进制位串

请注意，JPEG文件中出现的DHT表仅定义每个位串长度的代码数，后跟所有代码字的序列。用于表示每个代码字的位串不包括在内！ JPEG解码器的工作是从提供的少量信息中导出这些位串。

存在许多方法，其中二进制串的生成在解码器中执行，并且它们中的大多数针对性能进行了大量优化（例如，djpeg霍夫曼例程）。这些实现很难学习。我发现通过手工绘制霍夫曼二进制树来生成这些位序列更具有指导意义。

在极端简化中，二叉树由根节点组成，该根节点具有到其他节点的左和右分支。这些节点中的每一个都可以是叶节点（分支的末尾）或者进一步分成两个节点。

JPEG文件中的实际DHT：

以下是使用JPEGsnoop直接从JPEG文件中的DHT（定义霍夫曼表，如上表2：Luminance AC中所示）中提取的。

 Class = 1 (AC Table)
  Destination ID = 0
    Codes of length 01 bits (000 total): 
    Codes of length 02 bits (002 total): 01 02 
    Codes of length 03 bits (001 total): 03 
    Codes of length 04 bits (003 total): 11 04 00 
    Codes of length 05 bits (003 total): 05 21 12 
    Codes of length 06 bits (002 total): 31 41 
    Codes of length 07 bits (004 total): 51 06 13 61 
    Codes of length 08 bits (002 total): 22 71 
    Codes of length 09 bits (006 total): 81 14 32 91 A1 07 
    Codes of length 10 bits (007 total): 15 B1 42 23 C1 52 D1 
    Codes of length 11 bits (003 total): E1 33 16 
    Codes of length 12 bits (004 total): 62 F0 24 72 
    Codes of length 13 bits (002 total): 82 F1 
    Codes of length 14 bits (006 total): 25 43 34 53 92 A2 
    Codes of length 15 bits (002 total): B2 63 
    Codes of length 16 bits (115 total): 73 C2 35 44 27 93 A3 B3 36 17 54 64 74 C3 D2 E2 
                                         08 26 83 09 0A 18 19 84 94 45 46 A4 B4 56 D3 55 
                                         28 1A F2 E3 F3 C4 D4 E4 F4 65 75 85 95 A5 B5 C5 
                                         D5 E5 F5 66 76 86 96 A6 B6 C6 D6 E6 F6 37 47 57 
                                         67 77 87 97 A7 B7 C7 D7 E7 F7 38 48 58 68 78 88 
                                         98 A8 B8 C8 D8 E8 F8 29 39 49 59 69 79 89 99 A9 
                                         B9 C9 D9 E9 F9 2A 3A 4A 5A 6A 7A 8A 9A AA BA CA 
                                         DA EA FA 
    Total number of codes: 162

那么，我们如何为每个代码创建二进制位串？

好吧，我们开始构建一个二叉树，创建新的分支并将代码字放入树的叶节点中。树的第1行包含仅需要1位编码的代码字，第2行包含仅需要2位编码的代码字（叶节点），依此类推。

我们首先从第0行开始：
##第0行（根节点）几乎总是父节点，创建一个向左和向右分支到下一行。我们标记左分支0和右分支1。
##在第1行，我们尝试用代码字填充任何节点（这个级别有2个），需要1位进行编码。我们从DHT看到，没有长度为1位的代码。因此，对于两个节点中的每一个，我们在下面（在第2行）产生左右节点，共创建4个节点。同样，对于这些分支，我们将左边的一个标记为0，右边标记为1。
##在第2行，我们将尝试从左到右填写任何长度为2位的代码。这次我们在DHT中看到有两个代码可以使用长度为2的位串进行编码。因此，我们将第一个代码值x01（十六进制）放在第一个节点中，使其成为叶节点（否）进一步的分支将来自它）。然后，我们取第二个代码值x02并将其放在第二个节点中，使其成为叶节点。此时，我们在树的这一行中还剩下两个节点，但DHT中没有列出这个位串长度的代码字。因此，我们为该行的每个剩余节点创建两个分支。由于剩下两个节点，这将创建总共4个分支，这意味着在二叉树的第三行中将再次有4个节点。
##在第3行，我们有四个节点可用，但DHT表示只有一个代码字使用3位进行编码。因此，我们将x03放在这些节点的最左边，我们为剩下的三个节点中的每一个创建分支（为第4行创建6个节点）。
##在第4行，我们有6个节点可用，但DHT表示只有3个代码字使用4位进行编码。这次我们终止了三个节点（使它们成为叶子节点），我们进一步将其他三个节点延伸到第5行。

这个过程一直持续到我们使用了DHT表中定义的所有代码字为止。下图显示了上述DHT前四行的扩展。

DHT的二叉树扩展

注意：我从VG了解到上述表示可能是“面向右”而不是“左向”

完成二叉树后，您可以通过组合从根节点向下的路径上的每个分支的位标签来读取每个代码字的位串。 例如，代码字0x04由二进制位串1011编码，因为我们需要从根节点获取分支1，从第1行的节点获取0，从第2行的节点获取1，从第3行的节点获取分支1。

这个过程可能非常费力，并且二叉树通常呈现难以完成的形状。 为了简化这一过程，我在JPEGsnoop中添加了一个功能DHT Expand，它确定了DHT表中出现的每个代码字的二进制位字符串。

下面是表格的前几行的扩展，使用JPEGsnoop并启用了DHT扩展模式。

Expanded Form of Codes:
    Codes of length 02 bits:
      00 = 01
      01 = 02
    Codes of length 03 bits:
      100 = 03
    Codes of length 04 bits:
      1010 = 11
      1011 = 04
      1100 = 00 (EOB)
    Codes of length 05 bits:
      11010 = 05
      11011 = 21
      11100 = 12
    Codes of length 06 bits:
      111010 = 31
      111011 = 41
    Codes of length 07 bits:
      1111000 = 51
	   ...
    Codes of length 15 bits:
      111111111000100 = B2
      111111111000101 = 63
    Codes of length 16 bits:
      1111111110001100 = 73
      1111111110001101 = C2
	   ...
      1111111111111100 = DA
      1111111111111101 = EA
      1111111111111110 = FA

真正的JPEG解码器中的实现极大地优化了这种机制，因为在用于处理32位字或字节的处理器中，位串搜索/解析过程不是一项简单的任务。他们中的大多数最终创建了大型查找表，用于定义特定位串/代码匹配的下限和上限。

更逼真的JPEG图像

显然，上面是一个非常简单的JPEG图像示例。但是，真实图像将具有您将遇到的一些其他特征：
##色度子采样 - 您可以预期大多数照片将具有2x1色度子采样，这意味着每个MCU的解码序列将是Y1 Y2 Cb Cr而不是Y Cb Cr。
## AC组件 - 与上述不同，您肯定会有非零的AC系数。在这种情况下，您通常会有一些非零值，最终将以ZRL（代码字0xF0）终止，表示运行16个零，然后可能是EOB（代码字0x00）。

在JPEG解码器页面中描述了关于具有色度子采样和其他因子的霍夫曼编码的一些更多细节。

JPEGsnoop详细解码输出

在上面显示的图像上运行JPEGsnoop，启用扫描段 - >详细解码选项，将显示以下输出：

*** Decoding SCAN Data ***
  OFFSET: 0x00000282
  Scan Decode Mode: Full IDCT (AC + DC)


    Lum (Tbl #0), MCU=[0,0]
      [0x00000282.0]: ZRL=[ 0] Val=[ -512] Coef=[00= DC] Data=[0x FC FF 00 E2 = 0b (11111100 11111111 1------- --------)] 
      [0x00000285.1]: ZRL=[ 0] Val=[    0] Coef=[01..01] Data=[0x E2 AF EF F3 = 0b (-1100--- -------- -------- --------)] EOB
                      DCT Matrix=[-1024     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]

    Chr(0) (Tbl #1), MCU=[0,0]
      [0x00000285.5]: ZRL=[ 0] Val=[    0] Coef=[00= DC] Data=[0x E2 AF EF F3 = 0b (-----01- -------- -------- --------)] EOB
      [0x00000285.7]: ZRL=[ 0] Val=[    0] Coef=[01..01] Data=[0x E2 AF EF F3 = 0b (-------0 1------- -------- --------)] EOB
                      DCT Matrix=[    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]

    Chr(0) (Tbl #1), MCU=[0,0]
      [0x00000286.1]: ZRL=[ 0] Val=[    0] Coef=[00= DC] Data=[0x AF EF F3 15 = 0b (-01----- -------- -------- --------)] EOB
      [0x00000286.3]: ZRL=[ 0] Val=[    0] Coef=[01..01] Data=[0x AF EF F3 15 = 0b (---01--- -------- -------- --------)] EOB
                      DCT Matrix=[    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]


    Lum (Tbl #0), MCU=[1,0]
      [0x00000286.5]: ZRL=[ 0] Val=[ 1020] Coef=[00= DC] Data=[0x AF EF F3 15 = 0b (-----111 11101111 111100-- --------)] 
      [0x00000288.6]: ZRL=[ 0] Val=[    0] Coef=[01..01] Data=[0x F3 15 7F FF = 0b (------11 00------ -------- --------)] EOB
                      DCT Matrix=[ 2040     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]

    Chr(0) (Tbl #1), MCU=[1,0]
      [0x00000289.2]: ZRL=[ 0] Val=[    0] Coef=[00= DC] Data=[0x 15 7F FF D9 = 0b (--01---- -------- -------- --------)] EOB
      [0x00000289.4]: ZRL=[ 0] Val=[    0] Coef=[01..01] Data=[0x 15 7F FF D9 = 0b (----01-- -------- -------- --------)] EOB
                      DCT Matrix=[    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]

    Chr(0) (Tbl #1), MCU=[1,0]
      [0x00000289.6]: ZRL=[ 0] Val=[    0] Coef=[00= DC] Data=[0x 15 7F FF D9 = 0b (------01 -------- -------- --------)] EOB
      [0x0000028A.0]: ZRL=[ 0] Val=[    0] Coef=[01..01] Data=[0x 7F FF D9 00 = 0b (01------ -------- -------- --------)] EOB
                      DCT Matrix=[    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]
                                 [    0     0     0     0     0     0     0     0]