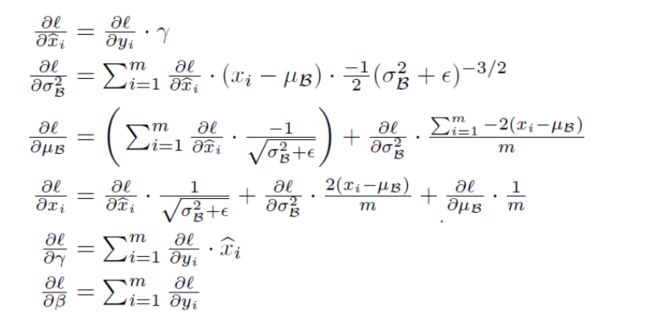cs231n-assignment2的笔记
重度拖延症患者准备继续完成作业2了......
首先题目链接点击打开链接
Q1: Fully-connected Neural Network (25 points)
在这一问中需要完成layers.py文件中的一些函数,首先是affine_forward,也就是前向计算,较为简单:
N = x.shape[0] x_reshape = x.reshape([N, -1]) x_plus_w = x_reshape.dot(w) # [N, M] out = x_plus_w + b然后是反向梯度传递计算,这里的一个小技巧就是先确定导数的表达式,然后具体计算(比如是否需要转置、求和等)则可以通过导数表达式中各项的shape确定,这个技巧在lecture4的backprop notes中Gradients for vectorized operations一节中有讲到。 点击打开链接
N = x.shape[0] x_reshape = x.reshape([N, -1]) # [N, D] dx = dout.dot(w.T).reshape(*x.shape) dw = (x_reshape.T).dot(dout) db = np.sum(dout, axis=0)
例如对于dx,通过上面前向计算表达式可知其导数为dout * w,由于dout.shape == (N, M),w.shape == (D, M),而dx.shape==(N, d1, ..., d_k),很容易写出表达式。
对于relu_forward,直接根据其表达式即可:
out = np.maximum(0, x)
而relu_backward中,则与点击打开链接 中的max gate是一致的,代码如下:
dx = dout * (x >= 0)接下来看看它在这次作业中预先实现好的svm loss和softmax loss。
实现Two-layer network, 这里较为简单,根据初始化要求,对w和b进行初始化:
self.params['W1'] = weight_scale * np.random.randn(input_dim, hidden_dim) self.params['b1'] = np.zeros(hidden_dim) self.params['W2'] = weight_scale * np.random.randn(hidden_dim, num_classes) self.params['b2'] = np.zeros(num_classes)
然后在loss函数中,搭建2层神经网络:
layer1_out, layer1_cache = affine_relu_forward(X, self.params['W1'], self.params['b1']) layer2_out, layer2_cache = affine_forward(layer1_out, self.params['W2'], self.params['b2']) scores = layer2_out
计算梯度:
loss, dscores = softmax_loss(scores, y) loss = loss + 0.5 * self.reg * np.sum(self.params['W1'] * self.params['W1']) + \ 0.5 * self.reg * np.sum(self.params['W2'] * self.params['W2']) d1_out, dw2, db2 = affine_backward(dscores, layer2_cache) grads['W2'] = dw2 + self.reg * self.params['W2'] grads['b2'] = db2 dx1, dw1, db1 = affine_relu_backward(d1_out, layer1_cache) grads['W1'] = dw1 + self.reg * self.params['W1'] grads['b1'] = db1
接下来将所有相关的内容全部利用一个solver对象来进行组合,其中solver.py中已经说明了该对象如何使用,所以在这里直接使用即可:
solver = Solver(model, data, update_rule='sgd', optim_config={ 'learning_rate': 1e-3,}, lr_decay=0.80, num_epochs=10, batch_size=100, print_every=100) solver.train() scores = solver.model.loss(data['X_test']) y_pred = np.argmax(scores, axis=1) acc = np.mean(y_pred == data['y_test']) print("test acc: ",acc)
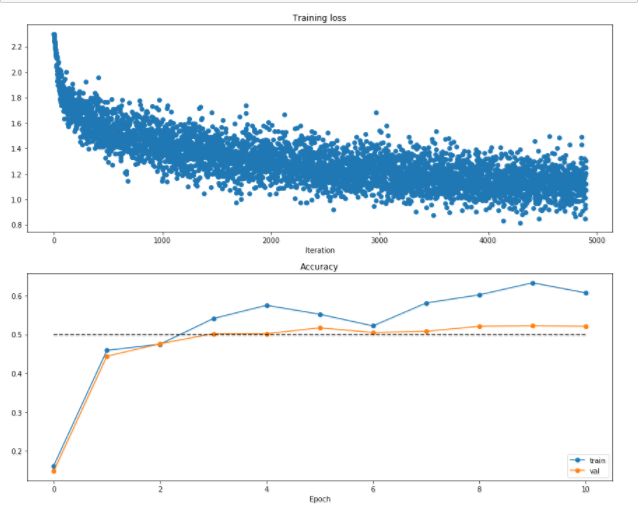
最终在测试集上达到的准确率为52.3%,然后做出图:
这里注意训练集和验证集的准确率,如果差别过大,而且验证集上准确率提升缓慢,则考虑是否过拟合。
然后是实现FullyConnectedNet,都是套路,网络层结构如下所示:
{affine - [batch norm] - relu - [dropout]} x (L - 1) - affine - softmax
在初始化中,对W、b、gamma、beta进行初始化,按照提示写即可:
shape1 = input_dim for i, shape2 in enumerate(hidden_dims): self.params['W'+str(i+1)] = weight_scale * np.random.randn(shape1, shape2) self.params['b'+str(i+1)] = np.zeros(shape2) shape1 = shape2 if self.use_batchnorm: self.params['gamma'+str(i+1)] = np.ones(shape2) self.params['beta'+str(i+1)] = np.zeros(shape2) self.params['W' + str(self.num_layers)] = weight_scale * np.random.randn(shape1, num_classes) self.params['b' + str(self.num_layers)] = np.zeros(num_classes)
loss的计算中注意加上正则化项,由于要考虑是否使用dropout层以及use_batchnorm,为方便起见,在layer_utils.py中加入一些函数
def affine_bn_relu_forward(x , w , b, gamma, beta, bn_param): a, fc_cache = affine_forward(x, w, b) bn, bn_cache = batchnorm_forward(a, gamma, beta, bn_param) out, relu_cache = relu_forward(bn) cache = (fc_cache, bn_cache, relu_cache) return out, cache def affine_bn_relu_backward(dout, cache): fc_cache, bn_cache, relu_cache = cache dbn = relu_backward(dout, relu_cache) da, dgamma, dbeta = batchnorm_backward_alt(dbn, bn_cache) dx, dw, db = affine_backward(da, fc_cache) return dx, dw, db, dgamma, dbeta
是否使用dropout层会影响梯度计算,所以中间变量利用两个dict保存,前向传递过程:
ar_cache = {}
dp_cache = {}
layer_input = X
for i in range(1, self.num_layers):
if self.use_batchnorm:
layer_input, ar_cache[i-1] = affine_bn_relu_forward(
layer_input, self.params['W'+str(i)], self.params['b'+str(i)],
self.params['gamma'+str(i)], self.params['beta'+str(i)], self.bn_params[i-1])
else:
layer_input, ar_cache[i-1] = affine_relu_forward(
layer_input, self.params['W'+str(i)], self.params['b'+str(i)])
if self.use_dropout:
layer_input, dp_cache[i-1] = dropout_forward(layer_input, self.dropout_param)
layer_out, ar_cache[self.num_layers] = affine_forward(
layer_input,self.params['W'+str(self.num_layers)], self.params['b'+str(self.num_layers)])
scores = layer_out
后向传递过程,基本上是将forward pass反向计算 :
loss, dscores = softmax_loss(scores, y) loss += 0.5 * self.reg * np.sum(self.params['W' + str(self.num_layers)] * self.params['W' + str(self.num_layers)]) dout, dw, db = affine_backward(dscores, ar_cache[self.num_layers]) grads['W'+str(self.num_layers)] = dw + self.reg * self.params['W' + str(self.num_layers)] grads['b'+str(self.num_layers)] = db for i in range(self.num_layers-1): layer = self.num_layers - i - 1 loss += 0.5 * self.reg * np.sum(self.params['W' + str(layer)] * self.params['W' + str(layer)]) if self.use_dropout: dout = dropout_backward(dout, dp_cache[layer-1]) if self.use_batchnorm: dout, dw, db, dgamma, dbeta = affine_bn_relu_backward(dout, ar_cache[layer-1]) grads['gamma' + str(layer)] = dgamma grads['beta' + str(layer)] = dbeta else: dout, dw, db = affine_relu_backward(dout, ar_cache[layer-1]) grads['W' + str(layer)] = dw + self.reg * self.params['W' + str(layer)] grads['b' + str(layer)] = db
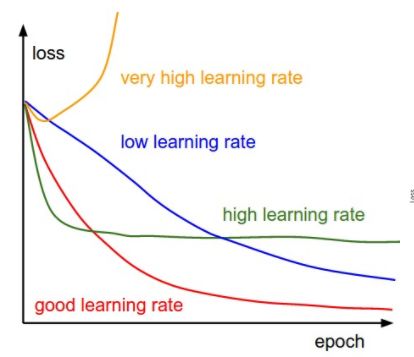
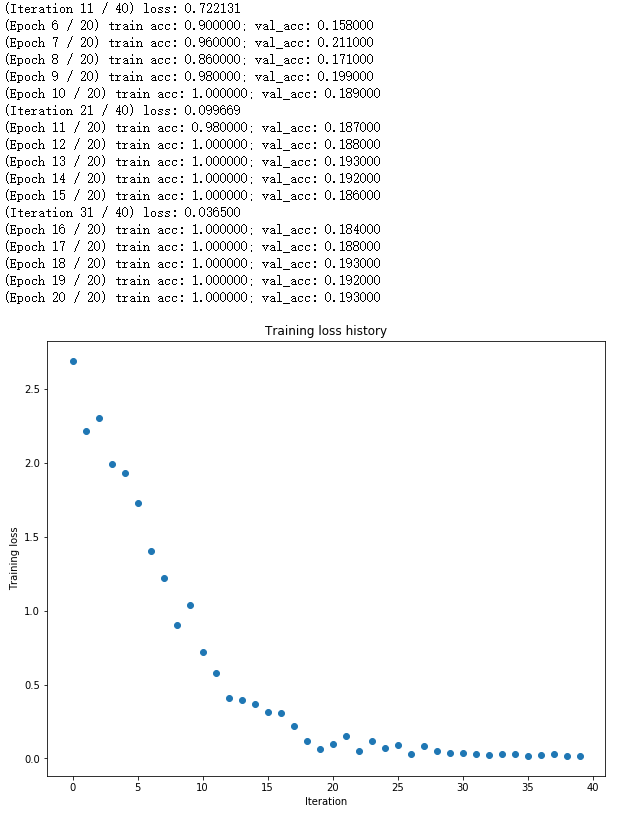
然后是在一个小样本集上进行训练,需要在20 epochs内达到100%的训练集准确率,初始的learning_rate是达不到要求的,所以需要调节该参数,这里的调参技巧是利用下图,引自cs231n的neural-networks-3 :
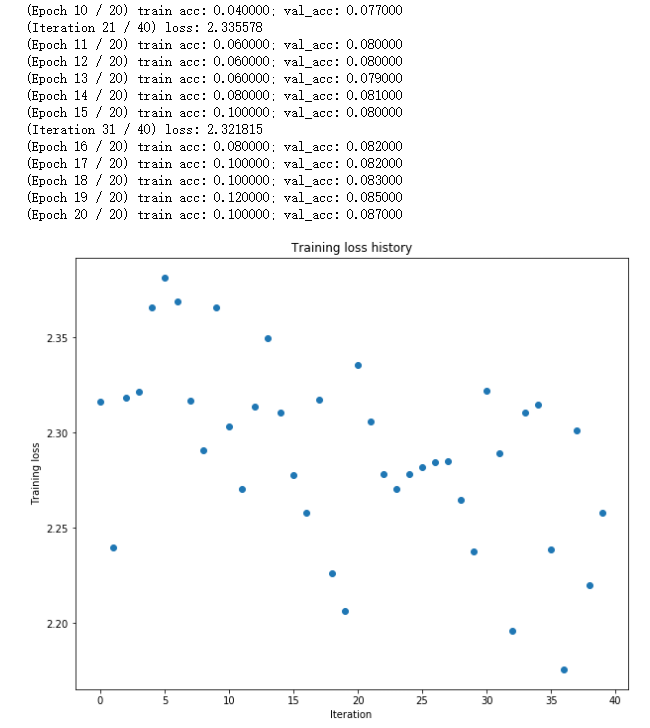
初始参数(1e-4)的结果如下:
可推测其学习率过低,适当增大学习率(1e-3、1e-2,先大范围搜索再小范围搜素)
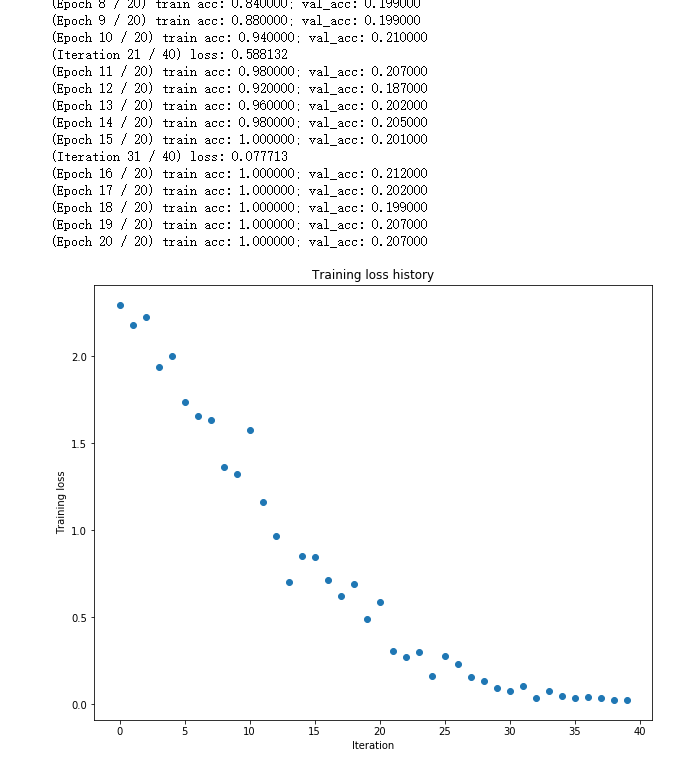
在learning_rate = 9e-3时结果如下:
然后是5层网络,也是需要调节lr和weight_scale,这里先调节lr,确定其大概范围后再对初始化值进行调节,但weight_scale对loss的影响是巨大的,这比前面的三层网络要复杂的多,最优参数也更加难以找到,最终learning_rate = 2e-2 , weight_scale = 4e-2:
但其实早已过拟合(看val_acc)......
下面是实现参数更新的几种方式,之前我们使用的方式是随机梯度下降(SGD,也即是利用minibatch更新一次可训练参数w、b等),首先第一种是SGD+Momentum(从这里开始属于lecture7的内容了):
这个可以直接根据notes上的代码写出:
v = config['momentum'] * v - config['learning_rate'] * dw next_w = w + v
rmsprop和adam的类似.
rmsprop:
config['cache'] = config['decay_rate'] * config['cache'] + (1 - config['decay_rate']) * (dx**2) next_x = x - config['learning_rate'] * dx / (np.sqrt(config['cache']) + config['epsilon'])
adam:
config['t'] += 1 config['m'] = config['beta1'] * config['m'] + (1 - config['beta1']) * dx config['v'] = config['beta2'] * config['v'] + (1 - config['beta2']) * (dx**2) mb = config['m'] / (1 - config['beta1']**config['t']) vb = config['v'] / (1 - config['beta2']**config['t']) next_x = x - config['learning_rate'] * mb / (np.sqrt(vb) + config['epsilon'])
Q2: Batch Normalization (25 points)
前向过程及其后向传播过程,这个可看论文中有详细推导:
主要公式如下:
代码如下:
sample_mean = np.mean(x , axis=0) # sample_mean's shape [D,] !!! sample_var = np.var(x, axis=0) # shape is the same as sample_mean x_norm = (x - sample_mean) / np.sqrt(sample_var + eps) out = gamma * x_norm + beta cache = (x, sample_mean, sample_var, x_norm, gamma, beta, eps) running_mean = momentum * running_mean + (1 - momentum) * sample_mean running_var = momentum * running_var + (1 - momentum) * sample_var
batchnorm_backward过程,较简单:
N, D = dout.shape x, sample_mean, sample_var, x_norm, gamma, beta, eps = cache dx_norm = dout * gamma dsample_var = np.sum(dx_norm * (-0.5 * x_norm / (sample_var + eps)), axis=0) dsample_mean = np.sum(-dx_norm / np.sqrt((sample_var + eps)), axis=0) + \ dsample_var * np.sum(-2.0/N * (x - sample_mean), axis=0) dx1 = dx_norm / np.sqrt(sample_var + eps) dx2 = dsample_var * (2.0/N) * (x - sample_mean) # from sample_var dx3 = dsample_mean * (1.0 / N * np.ones_like(dout)) # from sample_mean dx = dx1 + dx2 + dx3 dgamma = np.sum(dout * x_norm, axis=0) dbeta = np.sum(dout, axis=0)
然后是batchnorm_backward_alt,这个暂时没有找到比上面更快的方法,包括减少重复计算等,但效果不明显.......
后面的只需要跑相应的代码即可,fc_net.py中在Q1中已经实现了batchnorm......
Q3: Dropout (10 points)
dropout的代码在教程中都有实现:
mode == 'train'
mask = (np.random.rand(*x.shape) >= p ) / (1 - p)
out = x * mask
mode == 'test'
out = x
backward
dx = dout * mask然后实验发现dropout层的引入使得训练集准确率上升较慢,测试集准确率则更高,这说明其有效的防止了过拟合
Q4: Convolutional Networks (30 points)
首先是Convolution: Naive forward pass,与前面的是类似的,推荐画出相应的图来更易于写代码:
N, C, H, W = x.shape F, _, HH, WW = w.shape stride = conv_param['stride'] pad = conv_param['pad'] x_pad = np.pad(x, ((0,), (0,), (pad,), (pad,)), 'constant') out_h = 1 + (H + 2 * pad - HH) // stride out_w = 1 + (W + 2 * pad - WW) // stride out = np.zeros([N, F, out_h, out_w]) for j in range(out_h): for k in range(out_w): h_coord = min(j * stride, H + 2 * pad - HH) w_coord = min(k * stride, W + 2 * pad - WW) for i in range(F): out[:, i, j, k] = np.sum(x_pad[:, :, h_coord:h_coord+HH, w_coord:w_coord+WW] * w[i, :, :, :], axis=(1, 2, 3)) out = out + b[None, :, None, None]
然后是Convolution: Naive backward pass,这个其实就是逆过程,注意一点——对原forward pass的sum过程的处理:
db = np.sum(dout, axis=(0, 2, 3)) x, w, b, conv_param = cache N, C, H, W = x.shape F, _, HH, WW = w.shape stride = conv_param['stride'] pad = conv_param['pad'] x_pad = np.pad(x, ((0,), (0,), (pad,), (pad,)), 'constant') out_h = 1 + (H + 2 * pad - HH) // stride out_w = 1 + (W + 2 * pad - WW) // stride dx = np.zeros_like(x) dw = np.zeros_like(w) dx_pad = np.zeros_like(x_pad) for j in range(out_h): for k in range(out_w): h_coord = min(j * stride, H + 2 * pad - HH) w_coord = min(k * stride, W + 2 * pad - WW) for i in range(N): dx_pad[i, :, h_coord:h_coord+HH, w_coord:w_coord+WW] += \ np.sum((dout[i, :, j, k])[:, None, None, None] * w, axis=0) for i in range(F): dw[i, :, :, :] += np.sum(x_pad[:, :, h_coord:h_coord+HH, w_coord:w_coord+WW] * (dout[:, i, j, k])[:, None, None, None], axis=0) dx = dx_pad[:, :, pad:-pad, pad:-pad]
然后是max_pool_forward_naive:
N, C, H, W = x.shape ph, pw, stride = pool_param['pool_height'], pool_param['pool_width'], pool_param['stride'] out_h = 1 + (H - ph) // stride out_w = 1 + (W - pw) // stride out = np.zeros([N, C, out_h, out_w]) for i in range(out_h): for j in range(out_w): h_coord = min(i * stride, H - ph) w_coord = min(j * stride, W - pw) out[:, :, i, j] = np.max(x[:, :, h_coord:h_coord+ph, w_coord:w_coord+pw], axis=(2, 3))
而其backward过程的核心则是如何求解max的梯度,通过之前的学习可知max相当于一个屏蔽梯度的过程,它会将除了max值之外的所有数据的梯度变为0,所以由此可得:
x, pool_param = cache N, C, H, W = x.shape ph, pw, stride = pool_param['pool_height'], pool_param['pool_width'], pool_param['stride'] out_h = 1 + (H - ph) // stride out_w = 1 + (W - pw) // stride dx = np.zeros_like(x) for i in range(out_h): for j in range(out_w): h_coord = min(i * stride, H - ph) w_coord = min(j * stride, W - pw) max_num = np.max(x[:, :, h_coord:h_coord+ph, w_coord:w_coord+pw], axis=(2,3)) mask = (x[:, :, h_coord:h_coord+ph, w_coord:w_coord+pw] == (max_num)[:,:,None,None]) dx[:, :, h_coord:h_coord+ph, w_coord:w_coord+pw] += (dout[:, :, i, j])[:,:,None,None] * mask
后面的Three layer ConvNet过程则更加简单,直接堆叠函数即可:
__init__:这里需要注意的是W2的第一个参数的计算
C, H, W = input_dim self.params['W1'] = weight_scale * np.random.randn(num_filters, C, filter_size, filter_size) self.params['b1'] = np.zeros(num_filters) self.params['W2'] = weight_scale * np.random.randn((H//2)*(W//2)*num_filters, hidden_dim) self.params['b2'] = np.zeros(hidden_dim) self.params['W3'] = weight_scale * np.random.randn(hidden_dim, num_classes) self.params['b3'] = np.zeros(num_classes)
loss-forward pass:
layer1, cache1 = conv_relu_pool_forward(X, W1, b1, conv_param, pool_param) layer2, cache2 = affine_relu_forward(layer1, W2, b2) scores, cache3 = affine_forward(layer2, W3, b3)
loss-backward pass:
loss, dout = softmax_loss(scores, y) loss += 0.5*self.reg*(np.sum(W1**2)+np.sum(W2**2)+np.sum(W3**2)) dx3, grads['W3'], grads['b3'] = affine_backward(dout, cache3) dx2, grads['W2'], grads['b2'] = affine_relu_backward(dx3, cache2) dx, grads['W1'], grads['b1'] = conv_relu_pool_backward(dx2, cache1) grads['W3'] = grads['W3'] + self.reg * self.params['W3'] grads['W2'] = grads['W2'] + self.reg * self.params['W2'] grads['W1'] = grads['W1'] + self.reg * self.params['W1']
接下来是spatial_batchnorm的相关过程:
forward pass根据提示来做,求均值和方差均是对一张图的某一个像素点求,例如对于10张32*32*3的图片来说,分别对图片的每一位置求均值和方差(也就是10张图得到一张均值或方差图,其大小为32*32*3)
N, C, H, W = x.shape x2 = x.transpose(0, 2, 3, 1).reshape((N*H*W, C)) out, cache = batchnorm_forward(x2, gamma, beta, bn_param) out = out.reshape(N, H, W, C).transpose(0, 3, 1, 2)
backward pass:
N, C, H, W = dout.shape dout2 = dout.transpose(0, 2, 3, 1).reshape(N*H*W, C) dx, dgamma, dbeta = batchnorm_backward(dout2, cache) dx = dx.reshape(N, H, W, C).transpose(0, 3, 1, 2)