小白学习图像处理7——Hough变换检测直线

一、Hough变换的原理

1、过定点的直线方程

  在 xoy 平面给定一个点P(xi, yi)，则过点P的一条直线可以用表示为（直线x = C 除外）：
$$y_i=a{x}_i+b$$
  过点P的直线有无数条，它们构成一个集和，参数a、b满足方程：
$$b=-a{x}_i+y_i$$
  也就是说，参数a、b在一条直线上，直线斜率为-xi，截距为yi。把a、b构成的平面称为参数空间，因此：xoy平面内的一点确定参数空间的一条直线，下图展示了对应关系：，对应关系如下图所示：

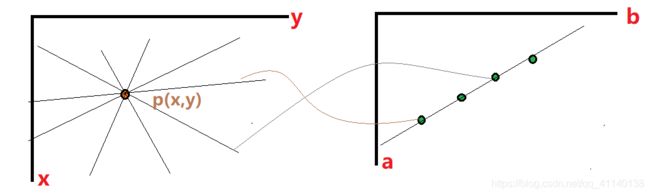
2、两点确定一条直线

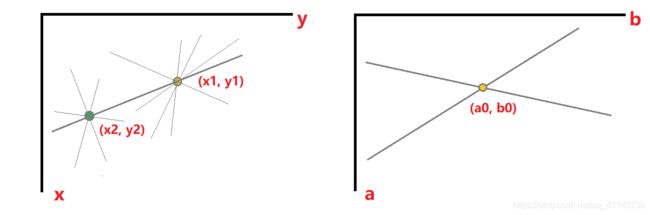
  如下图，若给定 xoy 平面内的两个点 P(x1, y1) 和 Q(x2, y2)，则在参数空间内我们可以确定两条直线，这两条直线交于一点 (a0, b0)，参数空间内点(a0, b0)对应着过两点的直线。
  参数空间内的一条直线对应着 xoy 平面的一个点，参数空间的一个点对应着 xoy 平面的一条直线。

3、方程的形式

  上面的结果说明了，我们可以在参数空间找直线的交点，反过来确定 xoy 平面的直线。前面的直线方程表达式为斜截式，斜截式存在一个问题，当直线的斜率很大的时候，截距趋于无穷，因此需要考虑别的形式。
  使用直线的 法线斜率 来表示直线可以巧妙地避开参数无穷大的问题（注意这个表达式不是极坐标表示）：

$$xcos\theta +ysin\theta =\rho$$

  其中，参数 ρ 表示原点到直线的距离，ρ∈[-D, D]，D 为图像的对角线长度，参数θ表示直线的法线与x轴的夹角，θ∈[-pi/4, pi/4]。对上式变一下形可得：

$$y=-xcot\theta +\rho /sin\theta$$

这个式子和斜截式一模一样，下图说明了它的几何意义：

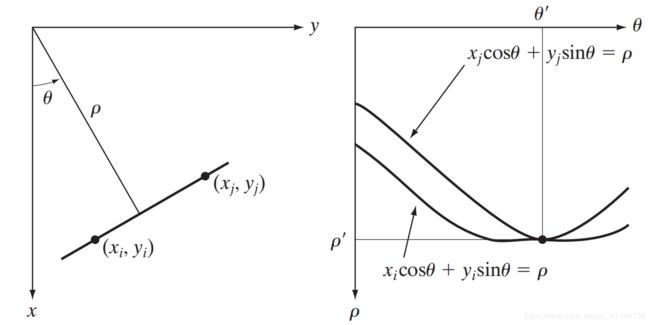
  解释：其中，对于点 (xi, yi) 来说，OB 表示ρ，0A代表 xi cosθ，AB表示 yi sin θ，于是xi cosθ + yi sinθ = ρ，由于点 (xi, yi) 是任意的，因此直线上每一点豆豆满足该方程（有没有觉得很直观）
  xoy 平面内的任意一个点都对应了一个方程，每一个方程确定了参数空间的一条 正弦波，若已知两个定点(xi, yi)，(xj, yi)，则在参数空间内对应的正弦波交于一点，该点确定了过两点的直线，如图：

---

二、实现过程

  上一部分给出了hough变换的理论基础，要在图像中检测直线还需要一定的处理。一幅图像对应着一系列的离散点，映射到参数平面一系列(ρ, θ)的组合，首先将ρθ参数空间划分为 累加单元，xy平面内一个点对于的参数空间的每一条曲线离散化为点，落在累加单元内，如下图所示：

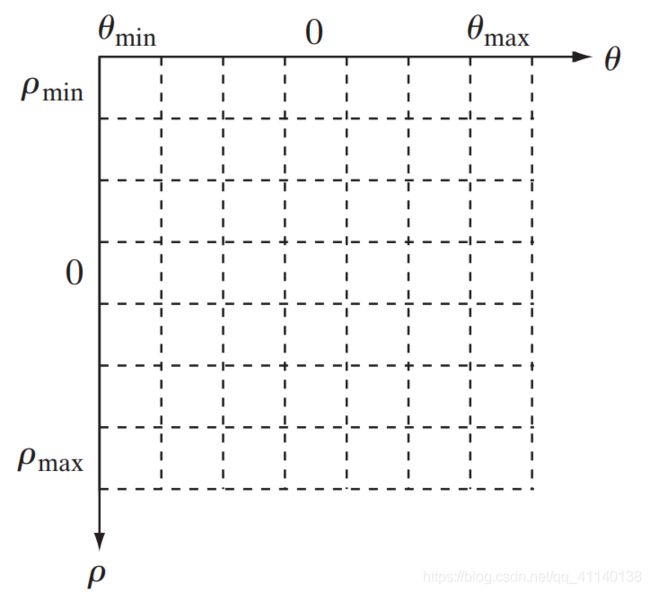
  坐标(i, j)处的单元具有累加值 A(i, j)，它对应于参数空间坐标(ρi, θj)相关联的正方形（我们对参数空间离散化为无数个正方形）

具体的步骤：

• 离散化ρθ参数空间，得到累加单元 A。
• 最初将所有累加单元的值A(i, j)置为零。
• 然后对于xoy平面内的每一个非背景点(xk, yk)，令 θ 等于 θ 轴上每一个允许的离散值，使用参数方程计算出 ρ 的对应值。对得到的 ρ 值四舍五入，得到最邻近的ρ轴上的离散值。对每一个非背景点，一个 θp 对于着 ρq ，则令A(p, q)加一。
• 完成上述步骤后，A(i, j)的值对应着xoy平面内有多少个点位于由参数(θ, ρ)确定的直线上。

---

三、程序代码

1、程序片段

提取边缘
为了检测直线，首先要提取图像的边缘，可以使用edge 函数提取图像边缘，假设读入的图像为灰度图：

img = imread(file_name);
img = im2double(img);
Edge = edge(img, 'canny', 0.2, 0.5, 1);
figure
subplot(121), imshow(img)
subplot(122), imshow(Edge)
set(gcf, 'color', [1 1 1])

结果如下：

---

参数平面离散化
  构建一个ρθ平面，并离散化为一个个方格，每一个小方格代表一个计数器，将计数器的值初始化为0，每个计数器对应的ρ-θ值确定了x-y平面内的一条直线（注意计数器的坐标与计数器对应的ρ-θ值的关系）：

[h, w] = size(Edge);
D = ceil(sqrt((h*h + w*w)));    % 对角线
d_rho = 2*D/precision;    % 单元大小
d_theta = pi/precision;    % 单元大小
rho = -D : d_rho : D;
theta = -pi/2 : d_theta : pi/2;

counter = zeros(length(rho), length(theta));  % ρ-θ平面计数器

---

累加器单元计数
  遍历图像的每一个像素点，如果该像素点上的灰度为1（edge函数得到一个二值图像，灰度为1说明像素点为非背景点），则通过点的坐标 (x, y) 得到 ρ-θ 平面内的一条直线，将 ρ-θ 内满足该直线方程的计数器的值加一：

rho_val = @(x, y, theta) x*cos(theta) + y*sin(theta);

for x = 1 : h 
    for y = 1 : w
        if Edge(x, y) == 1
            for theta_i = -pi/2 : d_theta : pi/2
                rho_i = rho_val(x, y, theta_i);
                rho_pos = round((rho_i + D) / d_rho + 1);             % 累加单元纵坐标
                theta_pos = round((theta_i + pi/2) / d_theta + 1);   % 累加单元横坐标
                counter(rho_pos, theta_pos) = counter(rho_pos, theta_pos) + 1;
            end
        end
    end
end

---

检测直线
  通过上面的计数过程，我们将 ρ-θ 平面当作图像绘制出来：

counter = counter / max(max(counter));    % 归一化
figure, imshow(counter)
set(gcf, 'color', [1 1 1])

结果如下，它是由很多条正弦曲线叠加得到的，多条曲线的交点就是直线的位置：

下面我们把最亮的那几个点提取出来：

counter = counter.*im2bw(counter, threshold);    % 将较暗的点置为0
% 亮的区域，只保留局部最大值
counter = counter.*(counter == ordfilt2(counter, domian_size.^2, ones(domian_size)));
counter = im2bw(counter, 0);
figure, imshow(counter)
set(gcf, 'color', [1 1 1])

结果如下：

最后一步，我们取出所有参数 (ρ, θ)

% 计算所有直线的参数
[rho_pos, theta_pos] = find(counter > 0);
theta_set = (theta_pos * d_theta - pi/2);   % theta 集合
rho_set = rho_pos * d_rho - D;                  % rho 集合

---

绘制直线
思路：遍历x-y平面内的所有像素点，如果x-y平面内的像素点(x0, y0) 坐标满足任意一对参数所确定的直线方程，则将原图像中的 (x0, y0) 像素点的灰度置为1：

%% 绘制边
for x = 1 : h
    for y = 1 : w
        % 判断点属于某条直线（满足某个直线方程）
        isLine = find(round(x*cos(theta_set) + y*sin(theta_set) - rho_set) == 0);
        if ~isempty(isLine)
            img(x, y) = 1;
        end
    end
end
figure, imshow(img)
set(gcf, 'color', [1 1 1])

结果如下：

---

2、总程序

  在程序的开始我们设定了三个参数，参数precision确定要把参数空间划分为多少格；参数threshold用于抑制参数平面内“较暗”的点；参数domian_size用于提取参数空间的局部最大值，确定直线。

close all

%% 参数
precision = 900;    % 控制精度，越大精度越高
threshold = 0.3;    % 控制可被检测的最小直线长度，越小可被检测到的线段越短
domian_size = 30;   % 避免重复的直线，适当大一些比较好
file_name = 'septagon.tif';

%% 提取边缘
img = imread(file_name);
img = im2double(img);
Edge = edge(img, 'canny', 0.2, 0.5, 1);
figure
subplot(121), imshow(img)
subplot(122), imshow(Edge)
set(gcf, 'color', [1 1 1])

%% 参数空间离散化
[h, w] = size(Edge);
D = ceil(sqrt((h*h + w*w)));    % 对角线
d_rho = 2*D/precision;    % 单元大小
d_theta = pi/precision;    % 单元大小
rho = -D : d_rho : D;
theta = -pi/2 : d_theta : pi/2;

counter = zeros(length(rho), length(theta));  % ρ-θ平面

%% 计数
rho_val = @(x, y, theta) x*cos(theta) + y*sin(theta);

for x = 1 : h 
    for y = 1 : w
        if Edge(x, y) == 1
            for theta_i = -pi/2 : d_theta : pi/2
                rho_i = rho_val(x, y, theta_i);
                rho_pos = round((rho_i + D) / d_rho + 1);             % 累加单元纵坐标
                theta_pos = round((theta_i + pi/2) / d_theta + 1);   % 累加单元横坐标
                counter(rho_pos, theta_pos) = counter(rho_pos, theta_pos) + 1;
            end
        end
    end
end

%% 检测边
counter = counter / max(max(counter));    % 归一化
figure, imshow(counter)
set(gcf, 'color', [1 1 1])

% 获得计数器值很大的边，抑制位置几乎相同的参数
counter = counter.*im2bw(counter, threshold);    % 只保留计数器值大的计数器
counter = counter.*(counter == ordfilt2(counter, domian_size.^2, ones(domian_size)));    % 抑制位置相近的参数
counter = im2bw(counter, 0);
figure, imshow(counter)
set(gcf, 'color', [1 1 1])

% 计算所有直线的参数
[rho_pos, theta_pos] = find(counter > 0);
theta_set = (theta_pos * d_theta - pi/2);   % theta 集合
rho_set = rho_pos * d_rho - D;                  % rho 集合

%% 绘制边
for x = 1 : h
    for y = 1 : w
        % 判断点属于某条直线（满足某个直线方程）
        isLine = find(round(x*cos(theta_set) + y*sin(theta_set) - rho_set) == 0);
        if ~isempty(isLine)
            img(x, y) = 1;
        end
    end
end
figure, imshow(img)
set(gcf, 'color', [1 1 1])

---

四、matlab 的hough函数

参考：小白学习图像处理——使用matlab的hough变换函数

---

完结~