Python语音基础操作--3.2短时时域分析

《语音信号处理试验教程》（梁瑞宇等）的代码主要是Matlab实现的，现在Python比较热门，所以把这个项目大部分内容写成了Python实现，大部分是手动写的。使用CSDN博客查看帮助文件：

Python语音基础操作–2.1语音录制，播放，读取
Python语音基础操作–2.2语音编辑
Python语音基础操作–2.3声强与响度
Python语音基础操作–2.4语音信号生成
Python语音基础操作–3.1语音分帧与加窗
Python语音基础操作–3.2短时时域分析
Python语音基础操作–3.3短时频域分析
Python语音基础操作–3.4倒谱分析与MFCC系数
Python语音基础操作–4.1语音端点检测
Python语音基础操作–4.2基音周期检测
Python语音基础操作–4.3共振峰估计
Python语音基础操作–5.1自适应滤波
Python语音基础操作–5.2谱减法
Python语音基础操作–5.4小波分解
Python语音基础操作–6.1PCM编码
Python语音基础操作–6.2LPC编码
Python语音基础操作–6.3ADPCM编码
Python语音基础操作–7.1帧合并
Python语音基础操作–7.2LPC的语音合成
Python语音基础操作–10.1基于动态时间规整(DTW)的孤立字语音识别试验
Python语音基础操作–10.2隐马尔科夫模型的孤立字识别
Python语音基础操作–11.1矢量量化(VQ)的说话人情感识别
Python语音基础操作–11.2基于GMM的说话人识别模型
Python语音基础操作–12.1基于KNN的情感识别
Python语音基础操作–12.2基于神经网络的情感识别
Python语音基础操作–12.3基于支持向量机SVM的语音情感识别
Python语音基础操作–12.4基于LDA，PCA的语音情感识别

代码可在Github上下载：busyyang/python_sound_open

时域分析就是提取语音信号的时域参数。时域分析通常用于最基本的参数分析与应用，如语音分割，预处理，分类等。常用的时域参数有短时能量，短时过零率，短时自相关系数和短时平均幅度差函数等。

1. 短时能量与短时平均幅度

设第$n$帧语音信号$x_n(m)$的短时能量用$E_n$表示：
$$E_n=\sum _{m=1}^N{x}_n^2(m)$$

$E_n$是度量语音信号幅度值变化的函数，对高电平非常敏感（用平方计算的）。可以用短时平均幅度函数$M_n$:
$$M_n=\sum _{m=1}^N|x_n(m)|$$

$M_n$也是一帧语音信号的能量大小的表征，不会应该平方造成较大差异。

2. 短时过零率

表示一帧语音信号波形穿过横轴的次数。也就是前后一个样本点符号变化的次数。
$$Z_n=\frac{1}{2}\sum _{m=1}^N|sgn[x_n(m)]-sgn[x_n(m-1)]|$$

在实际计算那种，由于信号中可能有50Hz的工频干扰或偏移量，计算的过零率参数往往不准确，所以在A/D转换前的防混叠带通滤波器的低端截止频率要高于50Hz，抑制电源干扰。在软件上去质量偏量，或者采用低直流漂移量元件。实际在计算过零率时候，还可以使用$x_i(m)\ast x_i(m+1)<0$来判断。

3. 短时自相关

自相关函数具有一些性质（如偶函数，如果序列是有周期性，自相关函数也有周期性）。对于浊音可以用自相关函数求出基音周期。在进行语音信号的预测分析时，也要用到自相关函数。语音信号$x_n(m)$的自相关函数$R_n(k)$可以表示为：
$$R_n(k)=\sum _{m=1}^{N-k}{x}_n(m)x_n(m+k)，其中(0⩽k⩽K)$$

K为最大延迟点数。短时自相关函数的性质有：

• 如果$x_n(m)$是周期的，假设周期为$N_p$，则自相关函数是同周期的周期函数，即$R_n(k)=R_n(k+N_p)$
• $R_n(k)$是偶函数，即$R_n(k)=R_n(-k)$
• 当$k=0$时，自相关函数具有最大值，即$R_n(0)⩾|R_n(k)|$，并且$R_n(0)$等于确定性信号序列的能量或随机性序列的平均功率。

4. 短时平均幅度差

短时自相关函数是语言信号分析的重要参量，但是计算自相关喊得运算非常大，为了避免乘法，一个简单的方法就是利用差值，即短时平均幅度差函数。因为如果信号是周期(周期为$N_p$)的，则相距的周期的整数倍的样本点的幅值是相等的，差值为0。
$$d(n)=x(n)-x(n+k)=0,(k=0,\pm N_p,\pm 2N_p,...)$$

实际语音信号$d(n)$不为零，是一个很小的值。可定义短时平均幅度差为：
$$F_n(k)=\sum _{m=1}^{N-k}|x_n(m)-x_n(m+k)|$$

如果$x(n)$在窗口范围内，具有周期性，则$F_n(k)$在$k=0,\pm N_p,\pm 2N_p,...$时将出现极小值。平均幅度差函数与自相关喊得关系为：
$$F_n(k)=\sqrt{2}\beta (k)[R_n(0)-R_n(k){]}^{1/2}$$

其中$\beta (k)$在不同的语音段在0.6~1.0之间变化，但是对一个特定的语音段，他随着$k$值的变化并不明显。

# timefeature.py
import numpy as np
from .C3_1_y_1 import enframe


def STAc(x):
    """
    计算短时相关函数
    :param x:
    :return:
    """
    para = np.zeros(x.shape)
    fn = x.shape[1]
    for i in range(fn):
        R = np.correlate(x[:, i], x[:, i], 'valid')
        para[:, i] = R
    return para


def STEn(x, win, inc):
    """
    计算短时能量函数
    :param x:
    :param win:
    :param inc:
    :return:
    """
    X = enframe(x, win, inc)
    s = np.multiply(X, X)
    return np.sum(s, axis=1)


def STMn(x, win, inc):
    """
    计算短时平均幅度计算函数
    :param x:
    :param win:
    :param inc:
    :return:
    """
    X = enframe(x, win, inc)
    s = np.abs(X)
    return np.mean(s, axis=1)


def STZcr(x, win, inc):
    """
    计算短时过零率
    :param x:
    :param win:
    :param inc:
    :return:
    """
    X = enframe(x, win, inc)
    X1 = X[:, :-1]
    X2 = X[:, 1:]
    s = np.multiply(X1, X2)
    sgn = np.where(s < 0, 1, 0)
    return np.sum(sgn, axis=1)


def STAmdf(X):
    """
    计算短时幅度差，好像有点问题
    :param X:
    :return:
    """
    # para = np.zeros(X.shape)
    fn = X.shape[1]
    wlen = X.shape[0]
    para = np.zeros((wlen, wlen))
    for i in range(fn):
        u = X[:, i]
        for k in range(wlen):
            en = len(u)
            para[k, :] = np.sum(np.abs(u[k:] - u[:en - k]))
    return para


def FrameTimeC(frameNum, frameLen, inc, fs):
    ll = np.array([i for i in range(frameNum)])
    return ((ll - 1) * inc + frameLen / 2) / fs

# C3_2_y.py
from scipy.io import wavfile
import matplotlib.pyplot as plt
from chapter3_分析实验.windows import *
from chapter3_分析实验.timefeature import *
from chapter2_基础.soundBase import *

data, fs = soundBase('C3_2_y.wav').audioread()
inc = 100
wlen = 200
win = hanning_window(wlen)
N = len(data)
time = [i / fs for i in range(N)]

EN = STEn(data, win, inc)  # 短时能量
Mn = STMn(data, win, inc)  # 短时平均幅度
Zcr = STZcr(data, win, inc)  # 短时过零率

X = enframe(data, win, inc)
X = X.T
Ac = STAc(X)
Ac = Ac.T
Ac = Ac.flatten()

Amdf = STAmdf(X)
Amdf = Amdf.flatten()

fig = plt.figure(figsize=(14, 13))
plt.subplot(3, 1, 1)
plt.plot(time, data)
plt.title('(a)语音波形')
plt.subplot(3, 1, 2)
frameTime = FrameTimeC(len(EN), wlen, inc, fs)
plt.plot(frameTime, Mn)
plt.title('(b)短时幅值')
plt.subplot(3, 1, 3)
plt.plot(frameTime, EN)
plt.title('(c)短时能量')
plt.savefig('images/energy.png')

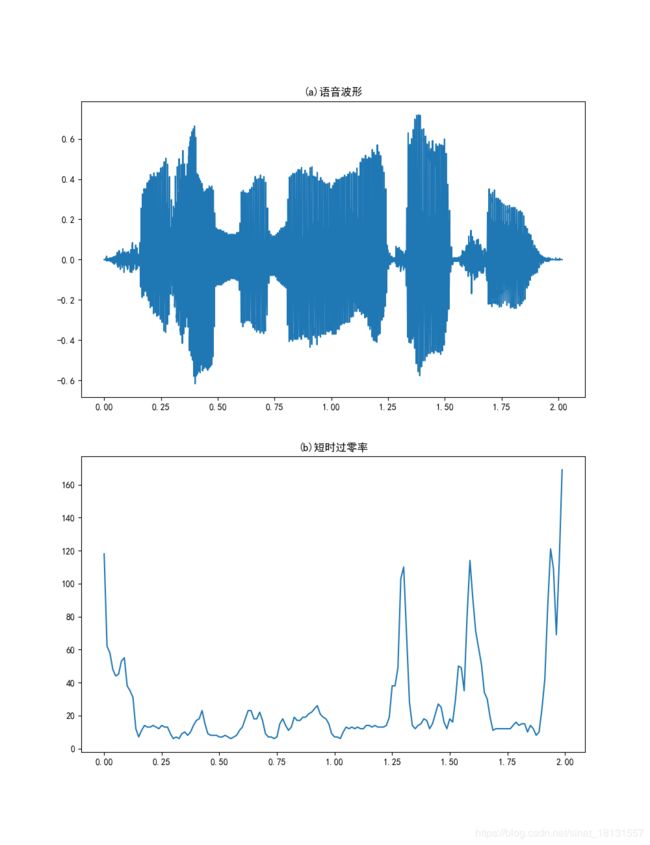
fig = plt.figure(figsize=(10, 13))
plt.subplot(2, 1, 1)
plt.plot(time, data)
plt.title('(a)语音波形')
plt.subplot(2, 1, 2)
plt.plot(frameTime, Zcr)
plt.title('(b)短时过零率')
plt.savefig('images/Zcr.png')

fig = plt.figure(figsize=(10, 13))
plt.subplot(2, 1, 1)
plt.plot(time, data)
plt.title('(a)语音波形')
plt.subplot(2, 1, 2)
plt.plot(Ac)
plt.title('(b)短时自相关')
plt.savefig('images/corr.png')

fig = plt.figure(figsize=(10, 13))
plt.subplot(2, 1, 1)
plt.plot(time, data)
plt.title('(a)语音波形')
plt.subplot(2, 1, 2)
plt.plot(Amdf)
plt.title('(b)短时幅度差')
plt.savefig('images/Amdf.png')