Python语音基础操作--3.3短时频域分析

《语音信号处理试验教程》（梁瑞宇等）的代码主要是Matlab实现的，现在Python比较热门，所以把这个项目大部分内容写成了Python实现，大部分是手动写的。使用CSDN博客查看帮助文件：

Python语音基础操作–2.1语音录制，播放，读取
Python语音基础操作–2.2语音编辑
Python语音基础操作–2.3声强与响度
Python语音基础操作–2.4语音信号生成
Python语音基础操作–3.1语音分帧与加窗
Python语音基础操作–3.2短时时域分析
Python语音基础操作–3.3短时频域分析
Python语音基础操作–3.4倒谱分析与MFCC系数
Python语音基础操作–4.1语音端点检测
Python语音基础操作–4.2基音周期检测
Python语音基础操作–4.3共振峰估计
Python语音基础操作–5.1自适应滤波
Python语音基础操作–5.2谱减法
Python语音基础操作–5.4小波分解
Python语音基础操作–6.1PCM编码
Python语音基础操作–6.2LPC编码
Python语音基础操作–6.3ADPCM编码
Python语音基础操作–7.1帧合并
Python语音基础操作–7.2LPC的语音合成
Python语音基础操作–10.1基于动态时间规整(DTW)的孤立字语音识别试验
Python语音基础操作–10.2隐马尔科夫模型的孤立字识别
Python语音基础操作–11.1矢量量化(VQ)的说话人情感识别
Python语音基础操作–11.2基于GMM的说话人识别模型
Python语音基础操作–12.1基于KNN的情感识别
Python语音基础操作–12.2基于神经网络的情感识别
Python语音基础操作–12.3基于支持向量机SVM的语音情感识别
Python语音基础操作–12.4基于LDA，PCA的语音情感识别

代码可在Github上下载：busyyang/python_sound_open

短时傅里叶变换

语音信号是典型的非平稳信号，但是由于其非平稳性由发声器官的物理运动过程而产生，这种过程是相对变换缓慢的，在10~30ms以内可以认为是平稳的。傅里叶分析时分析线性系统和平稳信号稳态特征的手段，而短时傅里叶分析，是用稳态分析方法处理非平稳信号的一种方法。

假设语音波形时域信号为$x(l)$,加窗分帧处理后得到的第$n$帧语音信号为$x_n(m)$,那有：
$$x_n(m)=w(m)x(n+m),1⩽m⩽N$$

对分帧信号进行短时傅里叶变化就是：
$$X_n(e^{jw})=\sum _{m=1}^N{x}_n(m)e^{-jwm}$$

其中，定义角频率$w=2\pi k/N$，得到了离散的短时傅里叶变化(DFT)。实际上就是$X_n(e^{jw})$在频域的取样：
$$X_n(e^{j\frac{2\pi k}{N}})=X_n(k)=\sum _{m=1}^N{x}_n(m)e^{-j\frac{2\pi km}{N}},1⩽k⩽N$$

实际中，可以使用FFT算法代替换成$x_n(m)$到$X_n(k)$的转换。

def STFFT(x, win, nfft, inc):
    xn = enframe(x, win, inc)
    xn = xn.T
    y = np.fft.fft(xn, nfft, axis=0)
    return y[:nfft // 2, :]

输入数据首先分帧处理，使用之前创建过的函数enframe(x, win, inc)。然后直接调用np.fft.fft(xn, nfft, axis=0)进行fft变化处理，中间有一个转置操作，是为了让时间轴作为横坐标，k作为纵坐标。

语谱图的表示

一般定义$|X_n(k)|$为$x_n(m)$的短时幅度谱估计，而时间处频谱能量密度函数$P(n,k)$表示为：
$$P(n,k)=|X_n(k){|}^2$$

可以看出$P(n,k)$是一个非负的实数矩阵，以时间n作为横坐标，k作为纵坐标，就可以绘制一张热图（或灰度图），这就是语谱图。如果通过$10\lg P(n,k)$处理后，语谱图的单位就是dB，将变换后的矩阵精细图像和色彩映射后，就能得到彩色的语谱图。

语谱图中的横杠表示他们是共振峰，从横杠对应的频率和宽度可以确定相应的共振峰的频率域带宽，在一个语音段中，有没有横杠的出现是判断是不是浊音的重要标志。竖条是语谱图中与时间轴垂直的条纹，每个竖直条表示一个基音，条纹的起点相当于声门脉冲的起点，条纹之间的距离表示基音周期。

在python中，读取到语音信号以后可以直接使用

plt.specgram(data, NFFT=256, Fs=fs, window=np.hanning(256))
plt.ylabel('Frequency')
plt.xlabel('Time(s)')
plt.show()

进行绘制语谱图，如果想要使用短时傅里叶变化得到的结果来做，那么首先看下输出的结果是一个复数矩阵，所以先求模np.abs(y)，那么用plt.matshow可以得到结果，不过这样的语谱图上下颠倒的，使用np.flip(np.abs(y), 0))上数据上下翻转一下。在绘制之前最好转化为dB单位，就是以10取对数，不然啥也看不见，黑乎乎一片。

from chapter3_分析实验.windows import *
from chapter3_分析实验.timefeature import *
from chapter2_基础.soundBase import *


def STFFT(x, win, nfft, inc):
    xn = enframe(x, win, inc)
    xn = xn.T
    y = np.fft.fft(xn, nfft, axis=0)
    return y[:nfft // 2, :]


data, fs = soundBase('C3_3_y.wav').audioread()

wlen = 256
nfft = wlen
win = hanning_window(wlen)
inc = 128

y = STFFT(data, win, nfft, inc)
freq = [i * fs / wlen for i in range(wlen // 2)]
frame = FrameTimeC(y.shape[1], wlen, inc, fs)

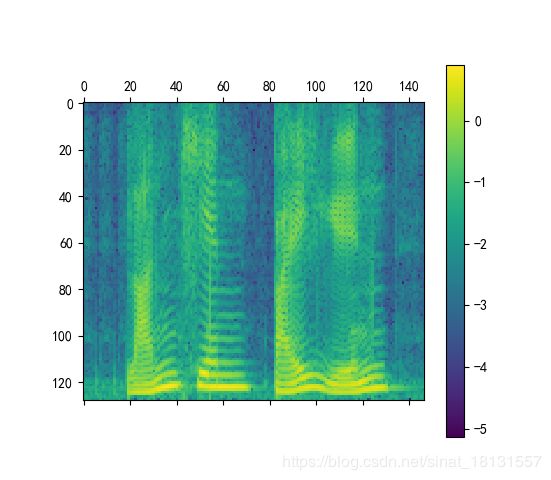
plt.matshow(np.log10(np.flip(np.abs(y), 0)))
plt.colorbar()
plt.show()

plt.specgram(data, NFFT=256, Fs=fs, window=np.hanning(256))
plt.ylabel('Frequency')
plt.xlabel('Time(s)')
plt.show()

得到的语谱图大约是这样的：