漫步微积分二十九——微积分基本定理

目前为止，我们通过逼近和的极限，得到了一个相当复杂的连续函数定积分的定义，

∫baf(x)dx=limmax Δxk→∞∑k=1nf(x∗k)Δxk(1)

之前我们已经用这个定义计算了一些简单的积分，例如

∫b0xdx=b22,∫b0x2dx=b33,and∫b0x3dx=b44(2)

这些计算有两个目的：通过提供一些逼近和的直观经验来强调积分的基本性质，并且这种方法得到的极限值可以作为计算其他积分的实用工具。那么，我们可以利用极限和的方方求解下面更复杂的积分吗？

∫10x47+x5−−−−−√3dxand∫21(1+1x)4dxx2(3)

这显然是不可能的，所以我们该何去何从呢？显然我们需要的是一种更高效、更强大的计算积分方法，而这种方法就是牛顿和莱布尼兹的想法。

牛顿-莱布尼兹解决(1)那样积分问题的计算方法乍一看似乎是自相矛盾的。为了解决这个问题，我们用更难的问题来替换它。我们不求解图1左那样固定的面积，而是图1右边变化的面积，图像右边的边界是可以移动的，这样的话面积就是 x 的函数。面积函数用 A(x) 表示，那么显然左边图中 A(a)=0,A(b) 表示固定的面积。我们的目标是找到一个 A(x) 的显示公式，然后通过设置 x=b 来确定所需的面积。在这个过程中有几个步骤，为了清楚起见，我们单独考虑。

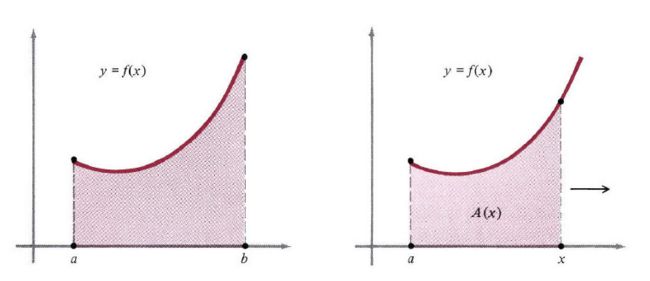
图1

步骤1：我们通过建立重要的事实

dAdx=f(x)(4)

开始。这是说面积 A 关于 x 的变化率等于区域右边界的长度。为了证明这个命题，我们必须考虑导数的定义

dAdx=limΔx→0A(x+Δx)−A(x)Δx

现在 A(x) 是图像下边 a,x 之间的面积， A(x+Δx) 是 a,x+Δx 之间的面积。因此，分子 A(x+Δx)−A(x) 是 a,x+Δx 之间的面积(看图2中阴影部分的面积)。很容易看出面积等于有着相同底，高为 f(x¯) 的矩形面积，其中 x¯ 是 x,x+Δx 之间的某个点。由它我们继续(4)的证明：

dAdx=limΔx→0A(x+Δx)−A(x)Δx=limΔx→0f(x¯)ΔxΔx=limΔx→0f(x¯)=f(x)

利用到 f(x) 是连续函数。为了更加详细的解释最后一步，我们指出 Δx→0 等价于 x+Δx→x ；因为 x¯ 位于 x,x+Δx 之间，所以 x¯→x ，现在利用函数的连续性得 f(x¯)→f(x)

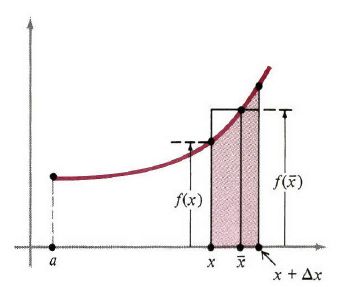
图2

步骤2：方程(4)告诉我们，找到面积函数 A(x) 就能实现我们的目标。根据(4)， A(x) 是函数 f(x) 的反导之一。但是，如果 F(x) 是任何一个 f(x) 的反导，根据前面不定积分的知识我们有

A(x)=F(x)+c(5)

c 是常数值。为了确定 c ，我们令 x=a ，从而得到 A(a)=F(a)+c ；但是因为 A(a)=0 ，从而得出 c=−F(a) 。因此

A(x)=F(x)−F(a)(6)

就是需要的公式。

步骤3：根据(6)和 A(x) 的意义，其余的工作就是观察

∫baf(x)dx=A(b)=F(b)−F(a)

我们用正式地微积分基本定理总结我们得到的结论：

如果 f(x) 是闭区间 [a,b] 上的连续函数，并且 F(x) 是 f(x) 的任何一个原函数，即 (d/dx)F(x)=f(x) 或等价地

∫f(x)dx=F(x)(7)

那么

∫baf(x)dx=F(b)−F(a)(8)

这个定理将计算极限和的问题转变成更容易的找原函数的问题，从而减小了评估定积分问题。因此，为了找出 ∫baf(x)dx 的值，我们没必要考虑求和；我们只是找到原函数即可，可以用任何方式如猜测、常规计算、巧妙计算或查书，然后计算 F(b)−F(a) 的值。

例如，在上篇文章中，我们利用许多代数技巧得到了公式(2)。现在，借助基本定理，下面简单的公式就像明显的事实：

∫b0xdx=b22,∫b0x2dx=b33,and∫b0x3dx=b44

更一般地，对任何指数 n>0 ，明显可以得出

∫baxndx=bn+1n+1−an+1n+1,because∫xndx=xn+1n+1

注解1： 在计算问题的过程中，使用括号是很方便的

F(x)∣∣ba=F(b)−F(a)(9)

符号的意思就是说： x 上限为 b 时的 F(x) 值减去 x 下限为 a 时的 F(x) 就是我们要找的数。例如 x2∣∣43=42−32=16−9=7 。利用这个符号，(8)可以写成

∫baf(x)dx=F(x)∣∣ba

注解2：从这次讨论中可以看出，任何 f(x) 的原函数都用(8)解决。如果对此还有疑问，那么回顾一下，如果 F(x) 是一个原函数，那么其他任何一个都可以通过添加一个常数 c 得到即 F(x)+c ；因为

F(x)+c∣∣ba=[F(b)+c]−[F(a)+c]=F(b)−F(a)

常数 c 对结果没有影响。因此当计算定积分要找原函数时，我们可以忽略常数。(然而，当我们要解决微分方程时，这些常量是不可或缺。)

例1：计算下面的定积分：

(a)∫2−1x4dx(b)∫161dxx√(c)∫278x√3dx(d)∫1413(x−13)10dx

解：通过观察每个原函数都比较容易得到：

(a)∫2−1x4dx=15x5∣∣2−1=15[32−(−1)]=335(b)∫161dxx√=2x√∣∣161=2(4−1)=6(c)∫278x√3dx=34x4/3∣∣278=34(81−16)=1954(d)∫1413(x−13)10dx=111(x−13)11∣∣1413=111(1−0)=111

基本定理在定积分和原函数之间建立了连接。该连接习惯使用积分符号表示原函数，就像(7)那样，并用不定积分替换了原函数。读者应该熟悉这些用法。从这个角度上，我们经常会放弃形容词(不定，定)，单独用积分一次表示函数(7)或数(8)，这需要上下文以及读者对所陈述事情的理解从而避免混淆。为了正确区分，我们强调定积分积分符号上有上下限，而不定积分从来没有这种。

我们对使用这种相似符号 ∫f(x)dx,∫baf(x)dx 从而对大家引起困惑感到很抱歉，虽然他们表示非常不同的概念。然而，这些符号经历了300多年，现在试图改变他们没有多大用处。几年前，一位作者试图引进符号 A[f(x)] 取代 ∫f(x)dx 。他的书比昨天报纸消失的都快。相反，学生有责任读懂符号 ∫f(x)dx,∫baf(x)dx 。就像我们认真阅读所有单词，从而可以区分类似于”peak”和”peek”，”venal”和”venal”，”manor”和“manner”，数学必须我们更加认真的阅读。

根据前面学习到的经验，我们知道(或许可以计算)许多不定积分和定积分我们都能求解。尤其是，定积分(3)也不是那么难计算了。

例2：计算

∫10x47+x5−−−−−√3dx

解：为了清楚起见，我们分别考虑不定积分。换元

u=7+x5du=5x4dx

从而

∫x47+x5−−−−−√3dx=∫(7+x5)−1/3x4dx=∫u−1/3(15du)=15∫u−1/3du=15⋅32u2/3=310(7+x5)2/3

利用基本定理得

∫10x47+x5−−−−−√3dx=310(7+x5)2/3∣∣10=310(4−72/3)=310(4−49−−√3)

例3：计算

∫21(1+1x)4dxx2

解：换元

u=1+1x,du=−dxx2

所以

∫(1+1x)4dxx2=∫u4(−du)=−15u5=−15(1+1x)5

根据基本定理

∫21(1+1x)4dxx2=−15(1+1x)5∣∣21=−15(24332−32)=781160

例4：求曲线 y=cosx 下面，从 x=0 到 x=b 所围成的面积，其中 0<b≤π/2

解：面积(看图1)可以用定积分给出

∫b0cosxdx

但是我们熟悉不定积分

∫cosxdx=sinx

所以我们立刻得出

∫b0cosxdx=sinx∣∣b0=sinb−sin0=sinb

与求极限和相比，可以清晰的看出基本定理的强大。之前极限和的计算很难，还要知道晦涩的三角恒等式，而知道了基本定理后，这里的计算依然很容易。

注解3：牛顿和莱布尼兹大约在同一时间相互独立的发现了微积分。然而，导数是切线的斜率和定积分是曲线下面积这些概念是在他们之前许多思想家都知道。在这种情况下，为什么是给予牛顿和莱布尼兹创建这个新数学分支的荣誉呢(该分支在西方文明的主要特征中，可以说是支柱)？主要是因为他们是微积分基本定理的主要发现者。他们理解到它的重要性，并开始构建所需的支撑材料，将其成功应用到科学和几何的问题上。

然而，科学历史学家将基本定理的根源追溯到早些时候Barrow 和Pascal的几何工作上，他们的著作影响了牛顿和莱布尼兹。正如牛顿(他不是一个谦虚的人)说过的：如果我看得更远，那是因为我站在巨人的肩膀上。这是他难得一次的自我贬低。这些巨人之一还有费马，他第一个证明图3所述的面积公式。这表明，他必须知道基本定理(这似乎是最便捷的方法)。但不幸的是他没有注意到它。

微积分基本定理无疑是人类思想最伟大的成就之一。当我们考虑数学和物理的后续发展在多大程度的取决于它时，它也是最有影响力的成就之一。在它被发现之前，从公元前三世纪的阿基米德到十七世纪中叶的费马，找出曲线面积、体积和长度问题非常困难，只有天才可能想着去解决他们，并且任何一代都只有少数人。但现在，牛顿、莱布尼兹以及他们的追随者在基本定理的基础上提出了大量的系统方法，之后我们会对这些问题进行探讨。

图3