线段树入门&lazy思想
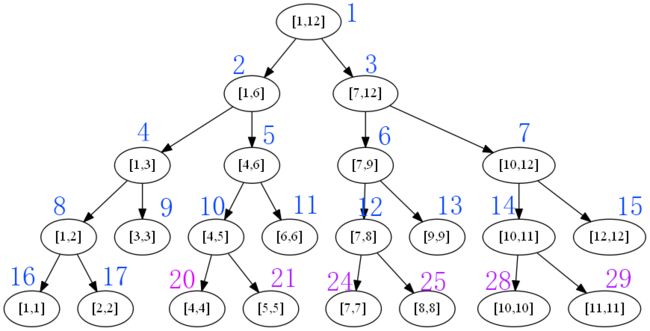
线段树将区间分成若干个子区间,子区间又继续分,直到区间为一个点(区间左值等于右值)
对于父区间[a,b],其子区间为[a,(a+b)/2]和[(a+b)/2+1,b]
用于求区间的值,如区间最值、区间的和等。
代码实现中,约定结点下标从1开始,所以某结点下标为x,那么左儿子下标为2x,右儿子下标为2x+1,父结点下标为x/2。
| 符号 | 等价 | 意义 |
|---|---|---|
| rt<<1 | rt*2 | 左子树的编号 |
| rt<<1|1 |
rt*2+1 | 右子树的编号 |
| (l+r)>>1 |
(l+r)/2 | 区间长度的一半 |
常用宏定义
#define Mid ((l+r)>>1) //注意括号
#define lson rt<<1,l,Mid //左结点
#define rson rt<<1|1,Mid+1,r //右结点建树
建树丛根结点开始,递归建立左右子树,直到叶子结点,然后反向赋值,父结点的值 = F(左结点的值,右结点的值),这个F是依据题意变的,如果是区间最大则为max()
void build(int rt,int l,int r) //建编号为rt的区间为[l,r]的树,主函数传进来的固定是(1,1,n)
{
if(l==r){ //叶子结点赋初值,注意下标,Max的是编号,val原数组的是l,看图可以理解
Max[rt] = val[l];
}else{ //建左右子树
build(lson);
build(rson);
Max[rt] = max( Max[rt<<1], Max[rt<<1|1]); //父结点Max值为Max(左子结点,右子结点)
}
}查询
查询为区间查询(只是查询某个点的话不需要线段树),即在区间里查询某个特性值,每次查询都是从跟结点开始往下,根据查询区间和当前区间的区间位置判断是要去左右子区间查询,还是直接返回。如果被查询区间是查询区间的子区间则直接返回子区间的值,如在[1,6]里查询[1,12]就返回[1,6]的值,不再往下查询。void query(int rt,int l,int r,int L,int R) //在[l,r]里查询[L,R]的值,[L,R]一直不变,[l,r]变
{
if(L <= l && r <= R){
ans1 = max(ans1,Max[rt]);
ans2 = min(ans2,Min[rt]);
}else{
if( L <= Mid) //查询区间在当前区间的左半区间有内容,如在[1,6]里查询[2,3]
query(lson,L,R);
if( R > Mid) //同理去右子区间,注意不能有else,因为有横跨左右的情况,如[1,6]里查询[2,5]
query(rson,L,R);
}
}更新
更新分为单点更新和区间更新,区间更新等会在下面讲述,而单点更新跟普通区间查询差不多
void update(int rt,int l,int r,int pos,int num)
{
if(l == r && r == pos){ //到对应的叶结点
Max[rt] = num;
}else{
if( pos <= Mid)
update(lson,pos,num);
if( pos > Mid) //或者直接else,点不可能同时在两个区间里
update(rson,pos,num);
Max[rt] = max( Max[rt<<1], Max[rt<<1|1]);
}
}数组大小要为原数据范围的4倍,证明点这里
题目
POJ 3264 Balanced Lineup 求区间的最大值-最小值
#include
#include
#include
using namespace std;
#define FOR( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define RE freopen("1.in","r",stdin);
#define bug(x) cout<<#x<<":"<<(x)<>1) //括号!
#define lson rt<<1,l,Mid
#define rson rt<<1|1,Mid+1,r
const int maxn= 50005;
const int inf=0x3f3f3f3f;
int Max[maxn<<2],Min[maxn<<2];
int ans1,ans2;
void build(int rt,int l,int r)
{
if(l==r){
scanf("%d",&Max[rt]);
Min[rt] = Max[rt];
}else{
build(lson);
build(rson);
Max[rt] = max( Max[rt<<1], Max[rt<<1|1]);
Min[rt] = min( Min[rt<<1], Min[rt<<1|1]);
}
}
void query(int rt,int l,int r,int L,int R)
{
if(L <= l && r <= R){
ans1 = max(ans1,Max[rt]);
ans2 = min(ans2,Min[rt]);
}else{
if( L <= Mid)
query(lson,L,R);
if( R > Mid)
query(rson,L,R);
}
}
int main()
{
int n,m,L,R;
while(scanf("%d%d",&n,&m)!=EOF){
build(1,1,n);
while(m--){
ans1 = -inf,ans2 = inf;
scanf("%d%d",&L,&R);
query(1,1,n,L,R);
printf("%d\n", ans1-ans2);
}
}
return 0;
}
HDU 1754 I Hate It单点更新,区间查询最大
#include
#include
#include
using namespace std;
#define FOR( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define RE freopen("1.in","r",stdin);
#define bug(x) cout<<#x<<":"<<(x)<>1)
#define lson rt<<1,l,Mid
#define rson rt<<1|1,Mid+1,r
const int maxn= 200000+5;
const int inf=0x3f3f3f3f;
int Max[maxn<<2];
int ans1,ans2;
void build(int rt,int l,int r)
{
if(l==r){
scanf("%d",&Max[rt]);
}else{
build(lson);
build(rson);
Max[rt] = max( Max[rt<<1], Max[rt<<1|1]);
}
}
void update(int rt,int l,int r,int pos,int num)
{
if(l == r && r == pos){
Max[rt] = num;
}else{
if( pos <= Mid)
update(lson,pos,num);
if( pos > Mid)
update(rson,pos,num);
Max[rt] = max( Max[rt<<1], Max[rt<<1|1]);
}
}
int query(int rt,int l,int r,int L,int R)
{
if(L <= l && r <= R){
return Max[rt];
}else{
int tmp = -1;
if( L <= Mid)
tmp = max(tmp,query(lson,L,R));
if( R > Mid)
tmp = max(tmp,query(rson,L,R));
return tmp;
}
}
int main()
{
// RE
int n,m,L,R;
char op;
while(scanf("%d%d",&n,&m)!=EOF){
build(1,1,n);
getchar();
while(m--){
scanf("%c%d%d%*c",&op,&L,&R);
if(op=='Q')
printf("%d\n",query(1,1,n,L,R));
else
update(1,1,n,L,R);
}
}
return 0;
}
HDU 1166 敌兵布阵
单点更新,查询区间和【此题树状数组解法转见→】
#include
#include
#include
using namespace std;
#define FOR( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define RE freopen("1.in","r",stdin);
#define bug(x) cout<<#x<<":"<<(x)<>1)
#define lson rt<<1,l,Mid
#define rson rt<<1|1,Mid+1,r
const int maxn= 50000+5;
const int inf=0x3f3f3f3f;
int sum[maxn<<2];
int ans1,ans2;
void build(int rt,int l,int r)
{
if(l==r){
scanf("%d",&sum[rt]);
}else{
build(lson);
build(rson);
sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
}
void update(int rt,int l,int r,int pos,int num)
{
if(l == r && r == pos){
sum[rt] += num;
}else{
if( pos <= Mid)
update(lson,pos,num);
else
update(rson,pos,num);
sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
}
int query(int rt,int l,int r,int L,int R)
{
if(L <= l && r <= R){
return sum[rt];
}else{
int tmp = 0;
if( L <= Mid)
tmp += query(lson,L,R);
if( R > Mid)
tmp += query(rson,L,R);
return tmp;
}
}
int main()
{
// RE
int n,m,L,R,t;
char op[10];
scanf("%d",&t);
for(int cas=1;cas<=t;cas++){
scanf("%d",&n);
build(1,1,n);
printf("Case %d:\n",cas);
while(scanf("%s",op),op[0]!='E'){
scanf("%d%d",&L,&R);
if(op[0]=='Q')
printf("%d\n", query(1,1,n,L,R));
else if(op[0]=='A')
update(1,1,n,L,R);
else
update(1,1,n,L,-R);
}
}
return 0;
}
区间成段更新
Lazy:正常来说,区间改值,当更改某个区间的值的时候,子区间也该跟着更改,这样容易TLE。
Lazy思想就是更新到某个区间的时候,就先给这个区间打上标记,标记内容是需要更新的值,并把子区间的值改为子区间对应的值,清除该区间的lazy标记;然后return,不去更新子区间。当下一次更新或查询等需要访问该区间的子区间的时候再把该区间的lazy和其他信息送回子区间。
举个简单粗暴的例子:
对应下面的那个图,假如目的是求和,现在要给[1,6] 的值都加2,那么我们从[1,12]->[1,6],然后[1,6]的sum值加上区间长度[ (6-1+1)*2 ],再把[1,6]的add[i]设置为2,就不再往下更新了【这里极大提高效率】。下一次更新/查询[1,6]的子区间时,我们将[1,6]原存的add值下传给[1,6]的两个直接子区间,再往下更新。假设在这种情况下,我们再更新[1,6]加3,则[1,6]的add值为2+3=5,然后我们查询[1,3],则从上往下经过[1,6]时把[1,6]的add值给了子区间[1,3]和[4,6],同时把sum[子区间]跟着子区间长度和add[父结点]改动,清除add[父节点]。【如果是查询间接子区间,则连续传递add值,也就是连续pushDown】
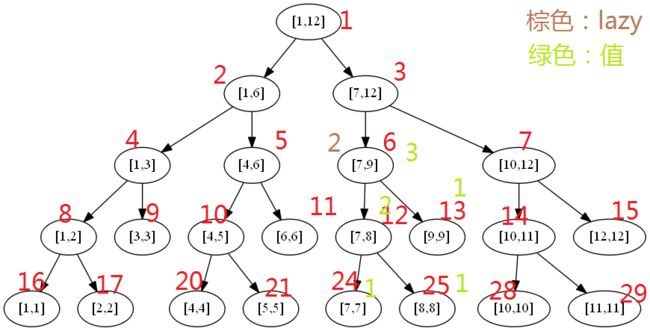
详细例子:假设update()是区间改值,query()是求和,所有叶子区间的和都为1,则[7,8]和[7,9]在build()的时候就附上了值(图中绿色字体)。假设此时我们更新[7,9]的值,改为2,则线段树从[1,12]->[7,12]->[7,9],然后把[7,9]打上值为2的标记,求和(求和直接用区间长度*此时更新的值),然后不去更新[7,8]和[9,9]了,他们值仍然是2和1,lazy值为0。
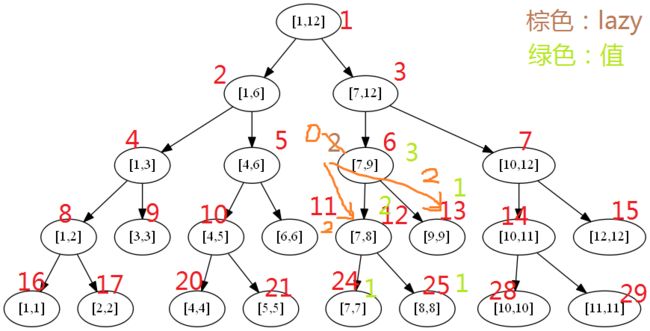
然后我们查询[7,8],当遍历经过[7,9]时
if(add[i])
pushDown(i);成立,把[7,9]的lazy标记2传给子区间[7,8]和[9,9],分别求这2个子区间的和,把[7,9]的lazy标记去掉,然后继续遍历,到[7,8]的时候直接返回答案。
HDU 1698 Just a Hook 区间改值,求和
#include
#include
#include
#include
using namespace std;
#define ll long long
#define FOR( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define RE freopen("1.in","r",stdin);
#define WE freopen("1.out","w",stdout);
#define MOD 10009
#define bug(x) cout<<#x<<":"<<(x)<>1)
#define lson rt<<1,l,Mid
#define rson rt<<1|1,Mid+1,r
const int maxn = 100010;
int sum[maxn<<2],add[maxn<<2];
void build(int rt,int l,int r)
{
add[rt] = 0;
if(l == r){
sum[rt] = 1;
}else{
build(lson);
build(rson);
sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
}
void pushDown(int rt,int len)
{
add[rt<<1] = add[rt<<1|1] = add[rt];
sum[rt<<1] = (len-(len>>1))*add[rt];
sum[rt<<1|1] = (len>>1)*add[rt];
add[rt] = 0;
}
void update(int rt,int l,int r,int L,int R,int z)
{
if(L <= l && r <= R){
add[rt] = z;
sum[rt] = (r-l+1)*z;
}else{
if(add[rt])
pushDown(rt,r-l+1);
if(L <= Mid)
update(lson,L,R,z);
if(R > Mid)
update(rson,L,R,z);
sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
}
int main()
{
// RE;
int t,n,q,x,y,z;
int cnt=1;
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&q);
build(1,1,n);
while(q--){
scanf("%d%d%d",&x,&y,&z);
update(1,1,n,x,y,z);
}
printf("Case %d: The total value of the hook is %d.\n", cnt++,sum[1]);
}
return 0;
}
相关链接:线段树题目合集 二维线段树 线段树模板