cs231n Lecture 5
说明
除特殊说明,本文以及这个系列文章中的所有插图都来自斯坦福cs231n课程。
转载请注明出处;也请加上这个链接http://vision.stanford.edu/teaching/cs231n/syllabus.html
Feel free to contact me or leave a comment.
Abstract
想不到我在2月初就已经看完了这个lecture. 看了我那天做的笔记,虽然寥寥草草,可也算简单的描述这个节课的主要内容。我对其加以整理,形成该文:Training Neural Networks.
我们前几次课已经学了简单的loss function以及optimazation相关的知识,并简单介绍了Neural Network.
Mini-batch SGD
Loop:
- Sample a batch of data
- Forward prop it through the graph, get loss
- Backprop to calculate the gradients
- Update the parameters using the gradient
Computational Graph,Chain rule.
Hint
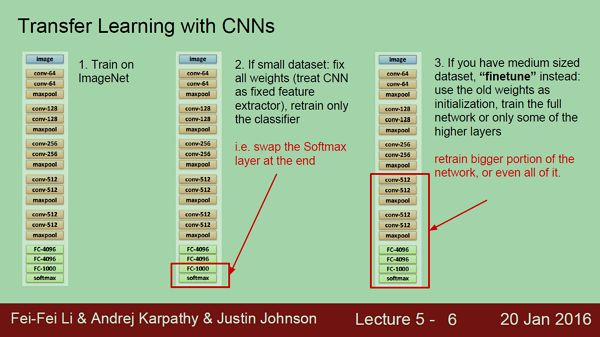
“ConvNets need a lot of data to train”
Finetuning! We rarely ever train ConvNets from scratch.
A bit of history
Frank Rosenblatt, ~1957: Perceptron
No back proportion.
Widrow and Hoff, ~1960: Adaline/Madaline
No back proportion.
Rumelhart et al. 1986: First time back-propagation became popular became popular
First time back-propagation became popular became popular
[Hinton and Salakhutdinov 2006]
First strong results
Context-Dependent Pre-trained Deep Neural Networks for Large Vocabulary Speech Recognition
George Dahl, Dong Yu, Li Deng, Alex Acero, 2010
Imagenet classification with deep convolutional neural networks
Alex Krizhevsky, Ilya Sutskever, Geoffrey E Hinton, 2012
Overview
这是接下来两节课的主要内容.
- One time setup
activation functions, preprocessing, weight
initialization, regularization, gradient checking - Training dynamics
babysitting the learning process,
parameter updates, hyperparameter optimization - Evaluation
model ensembles
Activation Functions
Sigmoid
- Squashes numbers to range [0,1]
- Historically popular since they have nice interpretation as a saturating “firing rate” of a neuron
3 problems:
- Saturated neurons “kill” the gradients
- Sigmoid outputs are not zerocentered
- exp() is a bit compute expensive
问题1是因为:What happens when x = -10?What happens when x = 0?What happens when x = 10?
Grdient在-10,10都是非常低,几乎0;在大的网络中,如果有些节点的梯度为0,那么它是无法back proportion的,也就意味着gradient vanishing.
问题2不太懂为什么数据要zerocentered. 但是结合下图的解释就是当输入x都是整数时,在back proportion时W的梯度要么全为正(输出为正)要么全为负(输出为负),这样在梯度更新的道路将是zig zag,这里也没太懂。
问题3,其实在CNN中计算消耗大多在卷积操作上;exp()这些都是小细节。
tanh(x)
- Squashes numbers to range [-1,1]
- zero centered (nice)
- still kills gradients when saturated
ReLU (Rectified Linear Unit)
- Computes f(x) = max(0,x)
- Does not saturate (in +region)
- Very computationally efficient
Converges much faster than sigmoid/tanh in practice
Not zero-centered output
- An annoyance:what is the gradient when x < 0?
ReLU更像是一个pass gate,如果x大于0,那么梯度为1,x小于0,那么梯度为0,并且这些数据将永远不会更新!恰好=0时,是一个未定义点,可以为0,也可以为1.
=> people like to initialize ReLU neurons with slightly positive biases (e.g. 0.01)
Leaky ReLU
- Does not saturate
- Computationally efficient
- Converges much faster than sigmoid/tanh in practice!
- will not “die”.
Parametric Rectifier (PReLU)
α在训练过程中像其它参数一样更新。
Exponential Linear Units (ELU)
- All benefits of ReLU
- Does not die
- Closer to zero mean outputs
- Computation requires exp()
Maxout “Neuron”
- Does not have the basic form of dot product ->nonlinearity
- Generalizes ReLU and Leaky ReLU
- Linear Regime! Does not saturate! Does not die!
Problem: doubles the number of parameters/neuron
In practice:
- Use ReLU. Be careful with your learning rates
- Try out Leaky ReLU / Maxout / ELU
- Try out tanh but don’t expect much
- Don’t use sigmoid
Data Preprocessing
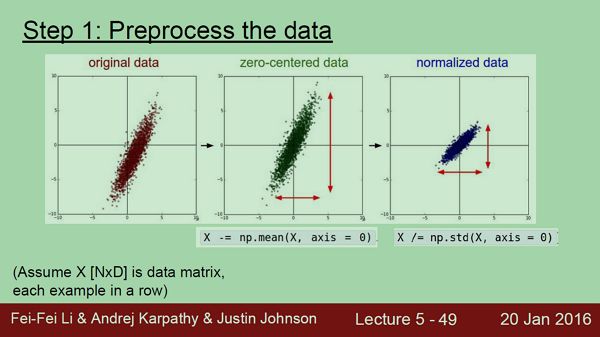
从下面这张slide看上看到,zero-centered就是减去均值mean.
除了上面两种,我们还常用到PCA and Whitening,但是尽管这种方式在机器学习中很常见,但是PCA and Whitening在神经网络对图像预处理中我们很少用,常用的就是下面Subtract the mean image and Subtract the per-channel mean这两种.
Not common to normalize variance, to do PCA or whitening
Weight Initialization
Q: what happens when W=0 init is used?
Small random numbers
(gaussian with zero mean and 1e-2 standard deviation)
Works ~okay for small networks, but can lead to non-homogeneous distributions of activations across the layers of a network.
E.g. 10-layer net with 500 neurons on each layer, using tanh nonlinearities
W = np.random.randn(fan_in,fan_out)*0.01 #layer initialization
All activations become zero!
Q: think about the backward pass. What do the gradients look like?
*1.0 instead of *0.01
W = np.random.randn(fan_in,fan_out)*1.0 #layer initialization
Almost all neurons completely saturated, either -1 and 1. Gradients will be all zero.
Reasonable initialization
(Mathematical derivation assumes linear activations)
“Xavier initialization” [Glorot et al., 2010]
He et al., 2015(note additional /2)
Proper initialization is an active area of research…
Understanding the difficulty of training deep feedforward neural networks by Glorot and Bengio, 2010
Exact solutions to the nonlinear dynamics of learning in deep linear neural networks by Saxe et al, 2013
Random walk initialization for training very deep feedforward networks by Sussillo and Abbott, 2014
Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification by He et al., 2015
Data-dependent Initializations of Convolutional Neural Networks by Krähenbühl et al., 2015 All you need is a good init, Mishkin and Matas, 2015
Batch Normalization
[Ioffe and Szegedy, 2015]
- compute the empirical mean and variance independently for each dimension.
- Normalize
Improves gradient flow through the network
Allows higher learning rates
Reduces the strong dependence on initialization
Acts as a form of regularization in a funny way, and slightly reduces the need for dropout, maybe
Babysitting the Learning Process
Step 1: Preprocess the data
Step 2: Choose the architecture
Loss barely changing: Learning rate is probably too low
Hyperparameter Optimization
Summary
We looked in detail at:
- Activation Functions (use ReLU)
- Data Preprocessing (images: subtract mean)
- Weight Initialization (use Xavier init)
- Batch Normalization (use)
- Babysitting the Learning process
- Hyperparameter Optimization (random sample hyperparams, in log space when appropriate)
- TODO
Look at:
- Parameter update schemes
- Learning rate schedules
- Gradient Checking
- Regularization (Dropout etc)
- Evaluation (Ensembles etc)