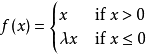常见激活函数原理及其图像python绘制（附源代码）

激活函数简介

神经网络中用于连接上层神经元输出与下层神经元输入的函数，根据不同的功能有不同的激活函数。

符号函数

符号函数简介

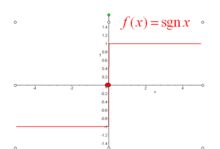
返回输入参数的正负号，用1指代+号，-1指代-号。

符号函数图象

定义公式

$$f(x)\{\begin{array}{ll}1,& x>0\\ 0,& x=0\\ -1,& x<0\end{array}$$

图像

Sigmoid函数

S型Sigmoid函数简介

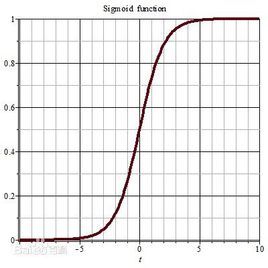
Sigmoid函数也称Logistic函数，由于其单增以及反函数单增，平滑且易于求导等优点，在计算机学科中，广泛用于神经网络激活函数以及逻辑回归，将变量映射到**(0，1)**间。

S型函数图像

定义公式

图象

双曲正切型Sigmoid激活函数

双曲正切型Sigmoid函数简介

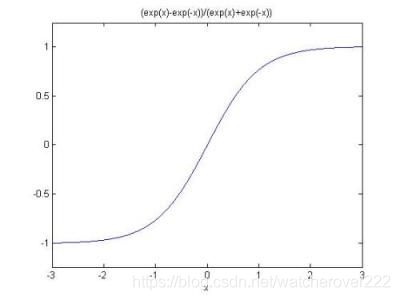
双曲正切函数（hyperbolic tangent function）是双曲函数的一种。双曲正切函数在数学语言上一般写作tanh，也可简写成th。双曲正切函数将输入值压缩在**(-1，1)**间。

定义公式

函数图像

图象

ReLu函数

函数简介

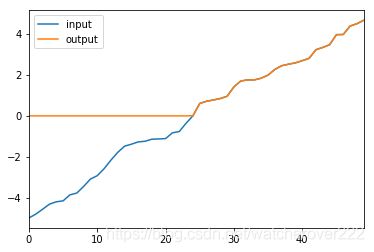
线性整流函数（Rectified Linear Unit, ReLU)，又称修正线性单元，是人工神经网络常用的激活函数。

函数图像

定义公式

f(x)=max(0, x)

拓展

线性整流函数在此基础上还有其他用于深度学习的变种，如带泄露线性整流(Leaky ReLU)，带泄露随机线性整流(Randomized Leaky ReLU)，以及噪声线性整流(Noisy ReLU)。

带泄露线性整流

在输入值为负数的时候，带泄露线性整流(Leaky ReLU)的梯度为一个常数λ∈（0，1），而不是0。即。

带泄露随机线性整流

带泄露随机线性整流（Randomized Leaky ReLU,RReLU）最早是在Kaggle全美数据科学大赛（NDSB）中被首先提出并使用的。相比于普通带泄露线性整流函数，带泄露随机线性整流在负输入值段的函数梯度是一个取自连续性均匀分布概率模型的随机变量，即,，其中。

噪声线性整流

噪声线性整流（Noisy ReLU）是修正线性单元在考虑高斯噪声的基础上进行改进的变种激活函数。对于神经元的输入值，噪声线性整流加上了一定程度的正态分布的不确定性，即，其中随机变量。

图象

线性分段函数

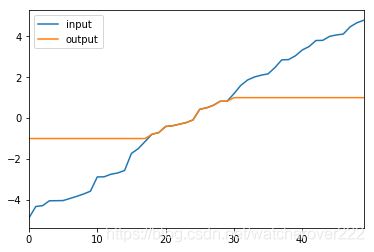
线性分段函数简介

可根据实际需要编写自己需要的线性分段激活函数。

公式

$$f(x)\{\begin{array}{ll}-1,& ifx\in (-\infty ,-1)\\ x,& ifx\in [-1,1]\\ 1,& ifx\in (1,+\infty )\end{array}$$

图象

代码

# -*- coding: utf-8 -*-
"""
Created on Tue Oct  8 20:09:49 2019

@author: C
"""

import numpy as np
import pandas as pd

def draw (type):
    inputs = np.random.uniform (-5, 5, 50)
    inputs.sort()
    if type == 'sigmoid':    
        outputs = sigmoid(inputs)
    elif type == 'tanh':
        outputs = tanh(inputs)
    elif type == 'relu':
        outputs = relu(inputs)
    elif type == 'sgn' :
        outputs = sgn(inputs.copy())
    else :
        outputs = piecewise (inputs.copy())
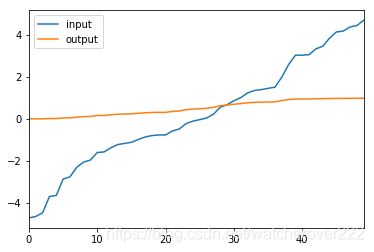
    df = pd.DataFrame(np.vstack((inputs, outputs))).T.rename(columns={0:'input',1:'output'})
    df.plot()
    return 
    
def sgn (x):
    mask = x>0
    x[mask] = 1
    mask = x==0
    x[mask] = 0
    mask = x<0
    x[mask] = -1
    return x
    
def piecewise (x):
    mask = x<-1
    x[mask] = -1
    mask = x>1
    x[mask] = 1
    return x

def tanh (x):
    return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))

def sigmoid (x):
    return 1.0/(1+np.exp(-x))

def relu (x):
    return np.maximum(x, 0)

type = input ()
draw (str(type))

reference

1.百度百科-relu函数.
2.百度百科-sigmoid函数.
3.百度百科-符号函数.

写在最后：

Il n’ya qu’un héroïsme au monde : c’est de voir le monde tel qu’il est et de l’aimer." Romain Rolland.