《MATLAB神经网络超级学习手册》——第2章 MATLAB基础 2.1 基本概念
本节书摘来自异步社区《MATLAB神经网络超级学习手册》一书中的第2章,第2.1节,作者:MATLAB技术联盟 , 刘冰 , 郭海霞著,更多章节内容可以访问云栖社区“异步社区”公众号查看
第2章 MATLAB基础
数据类型、常量与变量是MATLAB程序语言入门时必须引入的一些基本概念。数组是一种在高级语言中被广泛使用的构造型数据结构。在MATLAB中,为用户提供曲线拟合图形界面,用户可以在该界面上直接进行曲线拟合。
本章除了介绍以上内容外,还将简单介绍M文件中的一些概念。
2.1 基本概念
MATLAB神经网络超级学习手册
数据类型、常量与变量是程序语言入门时必须引入的一些基本概念,MATLAB 虽是一个集多种功能于一体的集成软件,但就其语言部分而言,这些概念同样不可缺少。
本节除了引入这些概念之外,还将介绍诸如向量、矩阵、数组、运算符、函数和表达式等概念。
2.1.1 MATLAB数据类型概述
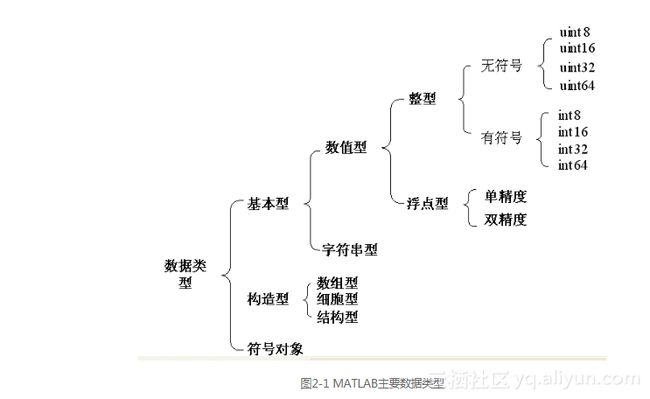
数据作为计算机处理的对象,在程序语言中可分为多种类型,MATLAB作为一种可编程的语言当然也不例外。MATLAB的主要数据类型如图2-1所示。
MATLAB数值型数据划分成整型和浮点型的用意和C语言有所不同。MATLAB的整型数据主要为图像处理等特殊的应用问题提供数据类型,以便节省空间或提高运行速度。对一般数值运算,绝大多数情况是采用双精度浮点型的数据。
MATLAB的构造型数据基本上与C++的构造型数据相衔接,但它的数组却有更加广泛的含义和不同于一般语言的运算方法。
符号对象是MATLAB所特有的一类为符号运算而设置的数据类型。严格地说,它不是某一类型的数据,它可以是数组、矩阵、字符等多种形式及其组合,但它在MATLAB的工作空间中的确又是另立的一种数据类型。
在使用中,MATLAB数据类型有一个突出的特点:在对不同数据类型的变量被引用时,一般不用事先对变量的数据类型进行定义或说明,系统会依据变量被赋值的类型自动进行类型识别,这在高级语言中是极有特色的。
提示:
这样处理的好处是,在书写程序时可以随时引入新的变量而不用担心会出什么问题,给应用带来了很大方便。但缺点是有失严谨,会给搜索和确定一个符号是否为变量名带来更多的时间开销。
2.1.2 常量与变量
常量是程序语句中取不变值的量,如表达式 y=0.618*x,其中就包含一个0.618这样的数值常数,它便是一数值常量。而另一表达式s='Tomorrow and Tomorrow'中,单引号内的英文字符串“Tomorrow and Tomorrow”则是一字符串常量。
在MATLAB中,有一类常量是由系统默认给定一个符号来表示的,例如pi,它代表圆周率π这个常数,即 3.1415926…,类似于C语言中的符号常量,这些特殊常量有时又称为系统预定义的变量,见表2-1。
变量是在程序运行中其值可以改变的量,变量由变量名来表示。在MATLAB中变量名的命名有自己的规则,可以归纳成如下几条。
(1)变量名必须以字母开头,且只能由字母、数字或者下画线3类符号组成,不能含有空格和标点符号(如( ),。%)等。
(2)变量名区分字母的大小写。例如,“a”和“A”是不同的变量。
(3)变量名不能超过63个字符,第63个字符后的字符被忽略,对于MATLAB 6.5版以前的变量名不能超过31个字符。
(4)关键字(如if、while等)不能作为变量名。
(5)最好不要用表2-1中的特殊常量符号作变量名。
2.1.3 标量、向量、矩阵与数组
标量、向量、矩阵和数组是MATLAB运算中涉及的一组基本运算量。它们各自的特点及相互间的关系可以描述如下。
(1)数组不是一个数学量,而是一个用于高级语言程序设计的概念。如果数组元素按一维线性方式组织在一起,那么称其为一维数组,一维数组的数学原型是向量。
如果数组元素分行、列排成一个二维平面表格,那么称其为二维数组,二维数组的数学原型是矩阵。
如果元素在排成二维数组的基础上,再将多个行、列数分别相同的二维数组叠成一个立体表格,便形成三维数组。依此类推下去,便有了多维数组的概念。
说明:
在MATLAB中,数组的用法与一般高级语言不同,它不借助于循环,而是直接采用运算符,有自己独立的运算符和运算法则。
(2)矩阵是一个数学概念,一般高级语言并未引入将其作为基本的运算量,但 MATLAB 是个例外。
一般高级语言是不认可将两个矩阵视为两个简单变量而直接进行加减乘除的,要完成矩阵的四则运算必须借助于循环结构。当MATLAB将矩阵引入作为基本运算量后,运算方式并没有完全遵守上述规定。MATLAB不仅实现了矩阵的简单加减乘除运算,而且许多与矩阵相关的其他运算也因此大大简化了。
(3)向量是一个数学量,一般高级语言中也未引入,它可视为矩阵的特例。从MATLAB的工作空间窗口可以查看到:一个n维的行向量是一个1×n 阶的矩阵,而列向量则当成n×1阶的矩阵。
(4)标量的提法也是一个数学概念,但在MATLAB中,一方面可将其视为一般高级语 言的简单变量来处理,另一方面又可把它当成1×1阶的矩阵,这一看法与矩阵作为MATLAB的基本运算量是一致的。
(5)在MATLAB中,二维数组和矩阵其实是数据结构形式相同的两种运算量。二维数组和矩阵的表示、建立、存储根本没有区别,区别只在它们的运算符和运算法则不同。
例如,向命令窗口中输入a=[1 2;3 4]这个量,实际上它有两种可能的角色:矩阵a或二维数组a。这就是说,单从形式上是不能完全区分矩阵和数组的,必须再看它使用什么运算符与其他量之间进行运算。
(6)数组的维和向量的维是两个完全不同的概念。数组的维是从数组元素排列后所形成的空间结构去定义的:线性结构是一维,平面结构是二维,立体结构是三维,当然还有四维以至多维。向量的维相当于一维数组中的元素个数。
下面介绍几个向量和矩阵的代数运算示例。
【例2-1】向量点积运算。
解:在MATLAB的Command Window窗口输入以下命令。
>> A=1:10;
>> B=linspace(1,10,10);
>> AT=A';
>> BT=B';
>> e=dot(A,B)
>> f=dot(AT,BT)
其运算结果如下。
e =
385
f =
385
在数学描述中,向量A、B的叉积是一新向量C,C的方向垂直于A与B所决定的平面。
【例2-2】合法向量叉积运算。
解:在Command Window窗口输入以下命令。
>>A=1:3,
>>B=3:5
>>E=cross(A,B) %该函数计算的是A、B叉积后各分量的元素值,且A、B只能是三维向量其运算结果如下。
A =
1 2 3
B =
3 4 5
E =
-2 4 -2
【例2-3】求给定矩阵的行列式值。
解:在Command Window窗口输入以下命令并得到其结果如下所示。
>> A=[3 2 4;1 -1 5;2 -1 3],D1=det(A)
A =
3 2 4
1 -1 5
2 -1 3
D1 =
24
>> B=ones(3),D2=det(B),C=pascal(4),D3=det(C)
B =
1 1 1
1 1 1
1 1 1
D2 =
0
C =
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
D3 =
1
【例2-4】已知矩阵A = left( {begin{array}{{20}c} 1 & 3 \ 2 & { - 1} \ end{array} } right),B = left( {begin{array}{{20}c} 3 & 0 \ 1 & 2 \ end{array} } right),求 A+B,2A,2A - 3B,AB。
解:在Command Window窗口输入以下命令。
>> A=[1 3;2 -1];
>>B=[3 0;1 2];
得到结果如下所示。
>> A+B
ans =
4 3
3 1
>> 2*A
ans =
2 6
4 -2
因为矩阵加减运算的规则是对应元素相加减,所以参与加减运算的矩阵必须是同阶矩阵。数与矩阵的加减乘除的规则很简单,但矩阵相乘有定义的前提是两矩阵内阶相等。
2.1.4 运算符
MATLAB运算符可分为3大类,即算术运算符、关系运算符和逻辑运算符。下面分类给出它们的运算符和运算法则。
1.算术运算符
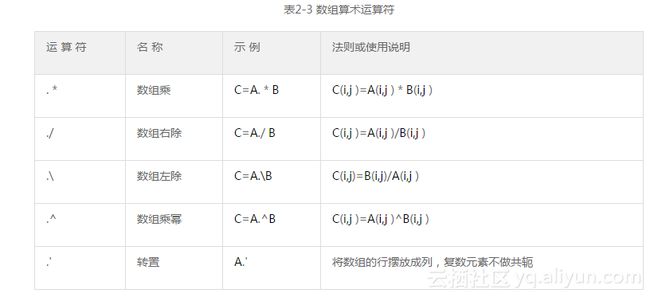
算术运算因所处理的对象不同,分为矩阵和数组算术运算两类。表 2-2给出的是矩阵算术运算的符号、名称、示例和使用说明,表2-3给出的是数组算术运算的符号、名称、示例和使用说明。
针对表2-2和表2-3需要说明以下几点。
(1)矩阵的加、减、乘运算是严格按矩阵运算法则定义的,而矩阵的除法虽和矩阵求逆有关系,但却分了左、右除,因此不是完全等价的。乘幂运算更是将标量幂扩展到矩阵可作为幂指数。总的来说,MATLAB接受了线性代数已有的矩阵运算规则,但又不仅止于此。
(2)表2-3中并未定义数组的加减法,是因为矩阵的加减法与数组的加减法相同,所以未做重复定义。
(3)不论是加减乘除,还是乘幂,数组的运算都是元素间的运算,即对应下标元素一对一的运算。
(4)多维数组的运算法则,可依元素按下标一一对应参与运算的原则将表2-3推广。
需要明确指出的是,MATLAB的关系运算虽可看成矩阵的关系运算,但严格地讲,把关系运算定义在数组基础之上更为合理。因为从表2-4所列法则不难发现,关系运算是元素一对一的运算结果。数组的关系运算向下可兼容一般高级语言中所定义的标量关系运算。
3.逻辑运算符
逻辑运算在MATLAB中同样需要,为此MATLAB定义了自己的逻辑运算符,并设定了相应的逻辑运算法则,见表2-5。
同样地,MATLAB的逻辑运算也是定义在数组的基础之上,向下可兼容一般高级语言中所定义的标量逻辑运算。为提高运算速度,MATLAB还定义了针对标量的先决与和先决或运算。
先决与运算是当该运算符的左边为1(真)时,才继续与该符号右边的量做逻辑运算。先决或运算是当运算符的左边为1(真)时,就不需要继续与该符号右边的量做逻辑运算,而立即得出该逻辑运算结果为1(真);否则,就要继续与该符号右边的量运算。
4.运算符的优先级
和其他高级语言一样,当用多个运算符和运算量写出一个MATLAB表达式时,运算符的优先次序是一个必须明确的问题。表2-6列出了运算符的优先次序。
MATLAB运算符的优先次序在表2-6中依从上到下的顺序,分别由高到低。而表中同一行的各运算符具有相同的优先级,而在同一级别中又遵循有括号先括号运算的原则。
2.1.5 命令、函数、表达式和语句
有了常量、变量、数组和矩阵,再加上各种运算符即可编写出多种MATLAB的表达式和语句。但在MATLAB的表达式或语句中,还有一类对象会时常出现,那便是命令和函数。
1.命令
命令通常就是一个动词,在第1章中已经有过接触,例如clear命令,用于清除工作空间。还有的可能在动词后带有参数,例如“addpath F:MATLAB文件M文件-end”命令,用于添加新的搜索路径。在MATLAB中,命令与函数都组织在函数库里,函数库general就是专门用来存放通用命令的。一个命令也是一条语句。
2.函数
函数对MATLAB而言,有相当特殊的意义,这不仅因为函数在MATLAB中应用面广,更在于其种类和数量多。仅就MATLAB的基本部分而言,其所包括的函数类别就达二十多个,而每一类中又有少则几个,多则几十个函数。
除了基本部分之外,还有各种工具箱,而工具箱实际上也是由一组组用于解决专门问题的函数构成。不包括MATLAB网站上外挂的工具箱函数,就目前MATLAB自带的工具箱已多达几十种,可见MATLAB其函数之多。从某种意义上说,函数就代表了MATLAB,MATLAB全靠函数来解决问题。
函数最一般的引用格式如下。
函数名(参数1,参数2,…)
例如,引用正弦函数就书写成sin(A),A就是一个参数,它可以是一个标量,也可以是一个数组,而对数组求其正弦是针对其中各元素求正弦,这是由数组的特征决定的。
3.表达式
用多种运算符将常量、变量(含标量、向量、矩阵和数组等)、函数等多种运算对象连接起来构成的运算式就是MATLAB的表达式。
例如,A+B&C -sin(A pi)就是一个表达式。请分析它与表达式(A+B)&C -sin(A pi)有无区别。
4.语句
在MATLAB中,表达式本身即可视为一个语句。而典型的MATLAB语句是赋值语句,其一般的结构如下。
变量名=表达式
例如,F=(A+B)&C-sin(A pi)就是一个赋值语句。
除赋值语句外,MATLAB还有函数调用语句、循环控制语句、条件分支语句等。这些语句将会在后面章节逐步介绍。