numpy5傅里叶变换示例

介绍

傅里叶这一张如果之后会用到，我会在进行扩展，这里先讲解最基本的用法。

定义

如我讲解有问题：希望各位指出。
这里有一个介绍傅里叶变换的博客，讲得很好，如果不知道傅里叶变换是什么，可以在这里看。https://www.cnblogs.com/h2zZhou/p/8405717.html
关键字解释：
傅里叶变换和反傅里叶变换是将声音在时域和频域之间的转换。
时域：以时间作为参照来观察动态世界的方法我们称其为时域分析。
频域：以震动频率为参照。
原文中以音乐和乐谱的关系来讲解时域和频域，其实是很容易让人误解的，因为乐谱毕竟也是按照时间先后顺序进行排列的。
但是频域不同，频域的概念更像你在同一时刻把乐谱上所有的声音都弹出来，而弹出来之后，声音会随着时间的变化自动变成你需要的音乐。因为两者之间的音符不同，频域的音符是连续的，是从头贯穿到尾的，但是时域的音符则是间断的，是只有那一时刻才有的。
很难理解，所以说文中这么形容频域：世界是永恒不变的
在频域的世界里，音乐在播放的第一时刻就已经决定了后面的所有的形容。

快速傅里叶变换模块（fft）

傅里叶定理：任何一个周期函数总可以被分解为若干不同振幅、频率和相位的正弦函数的叠加。
f(x) = 4/1pi sin(1x) + 4/3pi sin(3x) + 4/5pi sin(5x) +4/7pi sin(7x) + …
非周期函数可被视为周期无穷大的周期函数，傅里叶级数变成傅里叶积分。在工程上，从这些连续的频率中再选取离散的频率采样，得到离散化的频率序列，这就是离散傅里叶形式。

时间域的离散     ->      频率域的离散
x1->y1                        f1 -> A1 fai1     A1sin(f12pi x+fai1)
x2->y2                        f2 -> A2 fai2     A2sin(f22pi x+fai2)
...                                  ...
xn->yn                        fn -> An fain    Ansin(fn2pi x+fai2)
     \_________FFT变换_________^            +)------------------------
                                                                y = f(x)
    ^_______________IFFT反变换_________________/
import np.fft as nf
nf.fftfreq(时间域离散样本的个数，时间域离散样本的间隔（即采样周期）)
                                                        采样周期=1/采样频率
    ->频率域的离散样本系列(f1,f2,...,fn)，单位Hz
nf.fft([y1,y2,...,yn])->[(A1,fai1), (A2,fai2), ...]
                                         \     /
                                         a+bj
                                         模正比A1
                                         幅角就是fai1
nf.ifft([(A1,fai1), (A2,fai2), ...])->[y1,y2,...,yn]

import numpy as np
import numpy.fft as nf
import matplotlib.pyplot as mp
times = np.linspace(0, 2 * np.pi, 201)
#画五根曲线
sigs1 = 4 / (1 * np.pi) * np.sin(1 * times)
sigs2 = 4 / (3 * np.pi) * np.sin(3 * times)
sigs3 = 4 / (5 * np.pi) * np.sin(5 * times)
sigs4 = 4 / (7 * np.pi) * np.sin(7 * times)
sigs5 = 4 / (9 * np.pi) * np.sin(9 * times)
#将曲线结合在一起
sigs6 = sigs1 + sigs2 + sigs3 + sigs4 + sigs5
#时间-强度格式转换为频率-振幅的格式
# 频率序列，将数据按照这个序列展开
freqs = nf.fftfreq(times.size, times[1] - times[0])
# 强度（振幅）
ffts = nf.fft(sigs6)
print(ffts)
#获取振幅的值（即取模）
pows = np.abs(ffts)
print(pows)
# pows=ffts
#逆傅里叶变换
sigs7 = nf.ifft(ffts).real
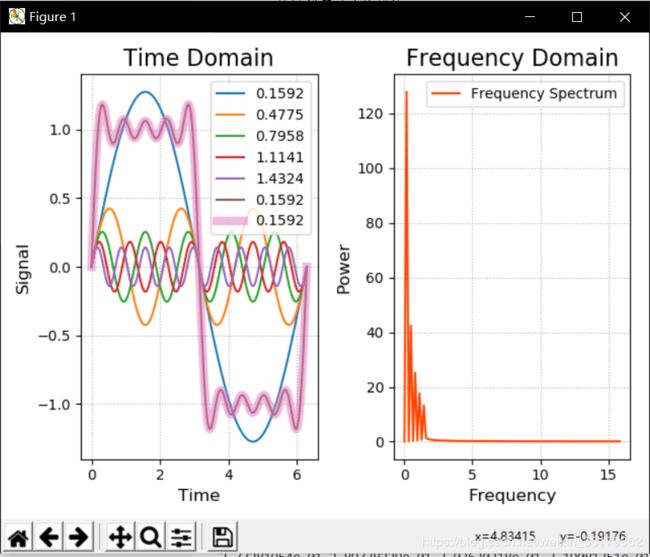
mp.subplot(121)
mp.title('Time Domain', fontsize=16)
mp.xlabel('Time', fontsize=12)
mp.ylabel('Signal', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(times, sigs1, label='{:.4f}'.format(
        1 / (2 * np.pi)))
mp.plot(times, sigs2, label='{:.4f}'.format(
        3 / (2 * np.pi)))
mp.plot(times, sigs3, label='{:.4f}'.format(
        5 / (2 * np.pi)))
mp.plot(times, sigs4, label='{:.4f}'.format(
        7 / (2 * np.pi)))
mp.plot(times, sigs5, label='{:.4f}'.format(
        9 / (2 * np.pi)))
mp.plot(times, sigs6, label='{:.4f}'.format(
        1 / (2 * np.pi)))
mp.plot(times, sigs7, label='{:.4f}'.format(
        1 / (2 * np.pi)), alpha=0.5, linewidth=6)
mp.legend()
mp.subplot(122)
mp.title('Frequency Domain', fontsize=16)
mp.xlabel('Frequency', fontsize=12)
mp.ylabel('Power', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(freqs[freqs >= 0], pows[freqs >= 0],
        c='orangered', label='Frequency Spectrum')
mp.legend()
mp.tight_layout()

mp.show()

实例：音频滤波

.wav文件记录一段声音在每一个采样时刻的位移，即位移关于时间的函数：s=f(t)，以时间域的方式表现声音。
数学中的函数：y = 3x^2+2x+1
计算机中的函数：多个存在对应关系的数组
1 2 3 4 5 …
6 17 34 57 86 …
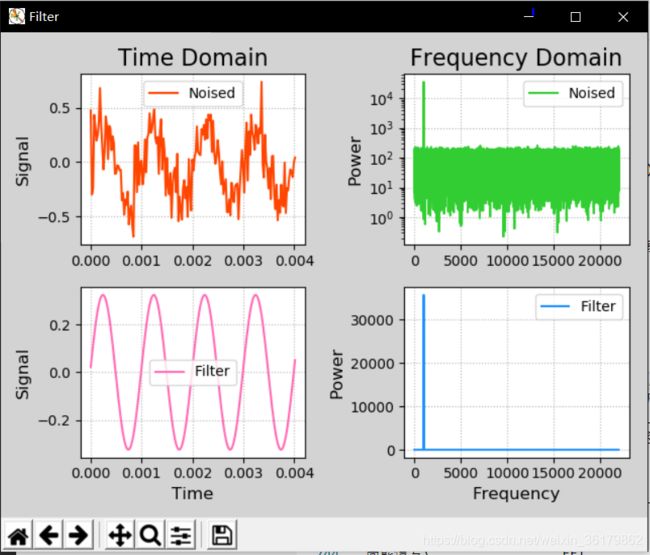
含有噪声的 FFT 含有噪声的 频率滤波 不含噪声的
时间域信号 -------> 频率域谱线 ----------> 频率域谱线

# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import numpy as np
import numpy.fft as nf
import scipy.io.wavfile as wf
import matplotlib.pyplot as mp
sample_rate, noised_sigs = wf.read(
    r'C:\Users\Cs\Desktop\数据分析\DS+ML\DS\data\noised.wav')
print(sample_rate,noised_sigs)
#存储的时候放大了2**15，（不然有些浮点数太小会直接被忽略？）所以这里先还原数值
noised_sigs = noised_sigs / 2 ** 15
#记录的次数，每个之间跨度为1/比率
times = np.arange(len(noised_sigs)) / sample_rate
print("times:",times)
print("rate:",sample_rate)
#频率序列
freqs = nf.fftfreq(times.size, 1 / sample_rate)
#进行傅里叶变换
noised_ffts = nf.fft(noised_sigs)
#获得复数的模，即振幅绝对值
noised_pows = np.abs(noised_ffts)
#armax()返回最大值的下标，将能量值较小的噪声过滤掉
fund_freq = np.abs(freqs[noised_pows.argmax()])
print("fund_freq:",fund_freq)
#生成筛子数组，这里是噪声的下标
noised_indices = np.where(np.abs(freqs) != fund_freq)
# 过滤噪声
filter_ffts = noised_ffts.copy()
filter_ffts[noised_indices] = 0
#过滤噪声之后的声音的模
filter_pows = np.abs(filter_ffts)
#逆傅里叶变换，得到的是类似： \
# 0.02333286-3.29975402e-17j格式的数据，这里过滤掉虚数部分，为啥要过滤掉虚数？？
filter_sigs = nf.ifft(filter_ffts).real
# 保存过滤后的数据
wf.write(r'C:\Users\Cs\Desktop\数据分析\DS+ML\DS\data\filter2.wav', sample_rate,
         (filter_sigs * 2 ** 15).astype(np.int16))
mp.figure('Filter', facecolor='lightgray')
mp.subplot(221)
mp.title('Time Domain', fontsize=16)
mp.ylabel('Signal', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(times[:178], noised_sigs[:178],
        c='orangered', label='Noised')
mp.legend()
mp.subplot(222)
mp.title('Frequency Domain', fontsize=16)
mp.ylabel('Power', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
#半对数坐标系，按照振幅值画折线。
mp.semilogy(freqs[freqs >= 0],
            noised_pows[freqs >= 0], c='limegreen',
            label='Noised')
mp.legend()
mp.subplot(223)
mp.xlabel('Time', fontsize=12)
mp.ylabel('Signal', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(times[:178], filter_sigs[:178],
        c='hotpink', label='Filter')
mp.legend()
mp.subplot(224)
mp.xlabel('Frequency', fontsize=12)
mp.ylabel('Power', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(freqs[freqs >= 0], filter_pows[freqs >= 0],
        c='dodgerblue', label='Filter')
mp.legend()
mp.tight_layout()
mp.show()