【反馈】传递函数（系统函数）----------来自《企业级编程与控制理论》
前言
相当简单的东西。关于方框图代数、拉普拉斯变换……
传递函数
y ( s ) = H ( s ) u ( s ) y(s) = H(s)u(s) y(s)=H(s)u(s)
输入/激励：u(s)
传递函数：H(s)
输出/响应：y(s)
H(s)传递函数不以任何方式依赖于外部“强制”函数u(s):它完全由微分方程独立确定。通过这种方式，它封装了系统所有内部动态特性。
微分方程包含的关于系统行为的所有信息，也都包含在传递函数中。由于H(s)仅仅是关于s的函数，比起微分方程，传递函数比较好用。
部分拉普拉斯编程的函数对应关系
| 时间空间f(t) | 频率空间F(s) |
|---|---|
| 1 | 1/s |
| t | 1/s2 |
| tn | n!/(sn + 1) |
| e(-t/T)/T | 1/(1+sT) |
| coswt | s/(s2 +w2) |
| sinwt | w/(s2+w2) |
| f(t) | F(s) |
| af(t)+bg(t) | aF(s)+bG(s) |
| eatf(t) | F(s-a) |
| f(t-T) | e-TsF(s) |
| f(t/a) | aF(as) |
| df(t)/dt | sF(s) - f(t=0) |
| \int_0^tf(u)du | F(s)/s |
方框代数
y ( s ) = G ( s ) ∗ H ( s ) u ( s ) y(s) = G(s)*H(s)u(s) y(s)=G(s)∗H(s)u(s)
对于系统G和系统H来说，G(s)和H(s)分别是各自的传递函数，而整体的传递函数就是G(s)*H(s)
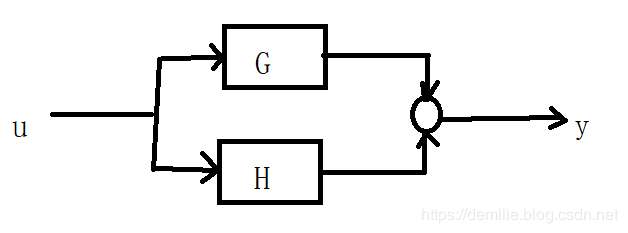
y ( s ) = G ( s ) u ( s ) + H ( s ) u ( s ) y(s) = G(s)u(s) + H(s)u(s) y(s)=G(s)u(s)+H(s)u(s)
这个系统整体的传递函数就是G(s) + H(s)
- 圆形○表示相加
- H表示受控系统，K表示控制器。-1方框是取y的相反数（有些系统中取相反数是在箭头旁画个负号，没有-1框）。
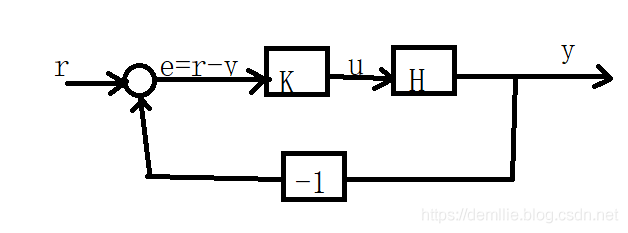
把K和H看做一个整体有 y = H K ( r − y ) y= HK(r - y) y=HK(r−y)推导出 y = H K 1 + H K r y = \frac{HK}{1+HK}r y=1+HKHKr
传递函数就是 H K 1 + H K \frac{HK}{1+HK} 1+HKHK
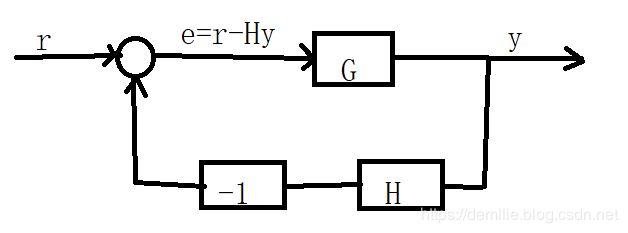
- G即是控制器也是受控系统，H是控制器
由 y = G ( r − H y ) y = G(r - Hy) y=G(r−Hy)有 y = G 1 + G H r y = \frac{G}{1 + GH}r y=1+GHGr
传递函数为 G 1 + G H \frac{G}{1+GH} 1+GHG
PID控制器
简单的反馈的控制器有两种，开关控制器（bang-bang）和三项控制器（PID）。当然，比三项控制器更复杂的比比皆是。
u p i d ( t ) = k p e ( t ) + k i ∫ 0 t e ( t ) d t + k d ∂ e ( t ) ∂ t u_{pid}(t) = k_pe(t)+k_i\int_0^te(t)dt+k_d\frac{\partial e(t)}{\partial t } upid(t)=kpe(t)+ki∫0te(t)dt+kd∂t∂e(t)
拉普拉斯变换得到频域下的表达式
u p i d ( s ) = [ k p + k i s + k d s ] e ( s ) u_{pid}(s) = [k_p + \frac{k_i}{s} + k_ds]e(s) upid(s)=[kp+ski+kds]e(s)
传递函数为
[ k p + k i s + k d s ] [k_p + \frac{k_i}{s} + k_ds] [kp+ski+kds]
另一种PID控制器传递函数形式为
k [ 1 + 1 s T i + s T d ] k[1+\frac{1}{sT_i} + sT_d] k[1+sTi1+sTd] k = k p T i = k p k i T d = k d k p k=k_p \;\;\;\;\;\;\;\;\;\;\;\;\;T_i = \frac{k_p}{k_i}\;\;\;\;\;\;\;\;\;\;\;\;\;T_d=\frac{k_d}{k_p} k=kpTi=kikpTd=kpkd
控制器参数变化的一般影响
K ( s ) = k p + k i s + k d s K(s)=k_p+\frac{k_i}{s}+k_ds K(s)=kp+ski+kds
- 增加 K p K_p Kp：增加速度，降低稳定性，增加噪音
- 增加 K i K_i Ki：降低速度，降低稳定性，减少噪声，消除稳态误差速度更快，增加振荡的幅度
- 增加 K d K_d Kd：增加速度，增加稳定性，快速增加噪音
比例控制器局限
error为零时控制器输出为零，这时调节不了。此时系统不一定稳定，即我仍然需要非零输出
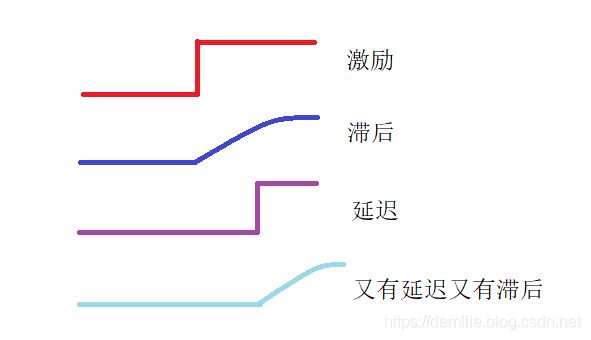
滞后与延迟
规定：滞后是给系统激励（输入）后马上反应，但是过一段时间才缓缓达到要求。延迟是给系统激励后过一段时间再反应。
（如果其他地方关于滞后和延迟的解释和这个不同的话，按其他的来）
通过微分方程得到传递函数：阶梯响应
前面说了传递函数与输入无关，所以传递函数是由齐次方程确定的，是零输入响应——至于为什么没有零状态和全响应，估计是这本书只取这种最简单的情况才能使能让传递函数和输入分离开。
对于系统的阶梯响应的动态特性，可以用微分方程 d y ( t ) d t + y ( t ) T = 0 \frac{dy(t)}{dt} + \frac{y(t)}{T}=0 dtdy(t)+Ty(t)=0来描述。其传递函数为 H ( s ) = 1 1 + s T H(s) = \frac{1}{1+sT} H(s)=1+sT1(这是标准化后的，即当s=0时，H(s)=1)
当输入是1时，1的拉布拉斯变换结果是 1 s \frac{1}{s} s1,则频域下的阶梯响应为
Y ( s ) = H ( s ) U ( s ) = 1 1 + s T 1 s = 1 s − T 1 + s T Y(s)=H(s)U(s)=\frac{1}{1+sT}\frac{1}{s}=\frac{1}{s}-\frac{T}{1+sT} Y(s)=H(s)U(s)=1+sT1s1=s1−1+sTT
时域下的阶梯响应为
y ( t ) = 1 − e − t / T y(t)=1-e^{-t/T} y(t)=1−e−t/T
很明显，这个响应是滞后的，还是简单的，因为没有振荡和冲击等行为。这样的简单滞后提供了任何缓慢过程的最简单的描述，是输出基本遵循其输入的过程。
斜波输入
仍然是上面那个传递函数，只不过输入换成 t t t 。于是 Y ( s ) = 1 1 + s T 1 s 2 = 1 s 2 − T s + T 2 1 + s T Y(s)=\frac{1}{1+sT}\frac{1}{s^2} =\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{1+sT} Y(s)=1+sT1s21=s21−sT+1+sTT2
时域下 y ( t ) = T ( t T − ( 1 − e − t / T ) ) y(t)=T(\frac{t}{T} - (1-e^{-t/T})) y(t)=T(Tt−(1−e−t/T))
斜波振荡器
外力驱动的阻尼振荡器： d 2 f ( t ) d t 2 + 2 ζ ω d y ( t ) d t + ω 2 y ( t ) = ω 2 f ( t ) \frac{d^2f(t)}{dt^2}+2\zeta\omega\frac{dy(t)}{dt}+\omega^2y(t)=\omega^2f(t) dt2d2f(t)+2ζωdtdy(t)+ω2y(t)=ω2f(t)
进行拉布拉斯变换后： s 2 Y ( s ) + 2 ζ ω s Y ( s ) + ω 2 Y ( s ) = ω 2 F ( s ) s^2Y(s)+2\zeta\omega sY(s)+\omega^2Y(s)=\omega^2F(s) s2Y(s)+2ζωsY(s)+ω2Y(s)=ω2F(s)
则斜波振荡器的传递函数为
H ( s ) = ω 2 s 2 + 2 ζ ω s + ω 2 H(s)=\frac{\omega^2}{s^2+2\zeta\omega s+\omega^2} H(s)=s2+2ζωs+ω2ω2
来自《企业级编程与控制理论》