计算机基础学习笔记 | 数据结构基础

学习资料

• 极客时间：数据结构与算法之美
• 《小灰的漫画算法之旅》

基础

• 数据结构：数据的组织、管理、存储格式，其目的是为了高效的访问和修改数据
• 算法：一系列程序指令，用于处理特定的运算和逻辑问题

十种常用数据结构

• 数组
• 链表
• 栈
• 队列
• 散列表
• 二叉树
• 堆
• 跳表
• 图
• Trie 树

十种常用的算法

• 递归
• 排序
• 二分查找
• 搜索
• 哈希算法
• 贪心算法
• 分治算法
• 回溯算法
• 动态规划
• 字符串匹配算法

时间复杂度

网图，侵权请联系删除

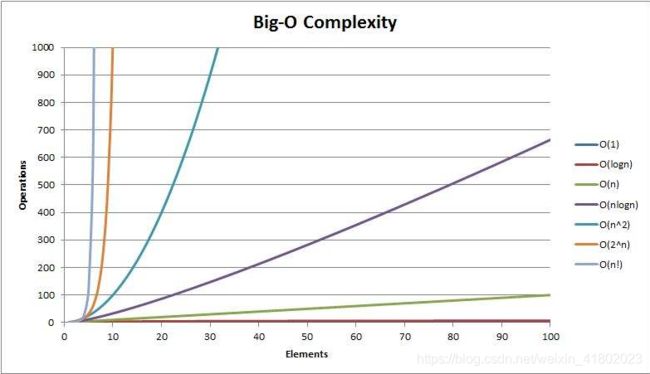
大O表达法，用来大概表示需要进行的时间

• 忽略低阶、常量、系数三部分并不左右增长趋势
  几个方法：
• 之关系循环次数最多的一段代码
• 加法法则：总复杂度等于量级最大的那段代码的复杂度
• 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

常见时间复杂度：

• 多项式量级
• 非多项式量级（O(2^n) 和 O(n!) ）

多项式时间复杂度

• O(1)

int i = 1;
int j = 2;
int sum = i + j;

• O(logn)

    i = 1;
    while(i <= n){
        i = i * 2;
    }

2^x = n,则 x = log2(n),忽略底数O(logn)

• O(m + n)、O( m * n)

由多个数据规模来决定时间复杂度：不能确定m、n的值，则为 O(m + n)

int cal(int m, int n) {
  int sum_1 = 0;
  int i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  int sum_2 = 0;
  int j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

空间复杂度

常见为O(1)、O(n)、O(n^2)

• 常量空间O(1)：算法的存储空间大小固定，和输入规模无直接关系
• 线性空间O(n)：线性集合（数组），且集合大小和输入规模n成正比
• 二维空间O(n^2)：二维数组
• 递归空间：与递归深度成正比

基础数据结构

数组 array

在内存中顺序存储（占用一片连续的内存地址）；每个元素有着自己的下标，可以通过下标查找元素；

• 数组插入、删除的时间复杂度：O(n)
• 数组查找、更新的时间复杂度：O(1)
• 优势：查找效率高，只需要给出下标
• 劣势：插入、删除效率低，需要移动大量元素

读取元素

因为数组在内存中顺序存储，所以可以直接通过下标读取到对应的数组元素 ，这种读取元素的方式叫做随机读取

 int[] array = new int[]{3,1,2,5,4,9,7,2}; 
 // 输出数组中下标为3的元素 
 System.out.println(array[3]);

更新元素

直接通过下标赋值

 int[] array = new int[]{3,1,2,5,4,9,7,2}; 
 // 给数组下标为5的元素赋值 
 array[5] = 10; 
 // 输出数组中下标为5的元素 
 System.out.println(array[5])

插入元素

存在三种情况

• 尾部插入
• 中间插入
• 超范围插入

尾部插入

直接插入到尾部空闲位置，等同于更新元素

中间插入

先把插入元素以及后面的元素向后移动，再将要插入的元素放到对应的数据位置

超范围插入

需要进行数组扩容：创建一个新的数组，再将旧数组的元素复制过去

删除元素

将元素逐个向左移位

链表 （linked list）

链表是一种在物理上非连续、非顺序的数据结构，由若干节点（node）所组成，在内存中的存储方式是随机存储；
单向链表的每一节点又包含两部分，一部分存放数据data，一部分是指向下一个节点的指针next；第一个节点成为头节点，最后一个节点称为尾节点
双向列表不仅拥有data、next部分，还存放指向前置节点的prev指针

查找节点

只能根据头节点开始向后一个一个节点逐一查找，时间复杂度：最坏的情况是O(n)

更新节点

如果不考虑查找节点的过程，链表更新直接替换新数据即可，时间复杂度O(n)

插入节点

• 尾部插入：把最后一个节点的next指针指向新插入的节点即可
• 头部插入：1、把新节点的next指向原头结点；2、把新节点变为链表的头节点
• 中间插入：1、新节点的next指向插入位置的节点；2、插入位置的前一个节点指向新节点

删除节点

• 尾部删除：尾节点直接指向空
• 头部删除：将头节点指向原头节点的next指针
• 中间删除：将要删除节点的前置节点指向要删除节点的下一个节点

数组和链表的对比

无	查找	更新	插入	删除
数组	O(1)	O(1)	O(n)	O(n)
链表	O(n)	O(1)	O(1)	O(1)

• 数组适合读取操作多、写操作少的场景
• 链表适合插入、删除多的情况
• 数组和链表都属于“物理结构”，是存在的存储结构；与之相对应的是逻辑结构，是抽象、依赖物理结构存在的

逻辑结构

• 栈
• 队列 （就像一个不封底的兵乓球桶，）
• 散列表

栈

• 就像一个封底的乒乓球桶，先放进去的后拿出来，即“先进后出”
• 可以用数组或者链表实现
• 入栈（push）：只允许栈顶一侧入栈，时间复杂度：O(1)
• 出栈（pop）：只允许栈顶元素出栈，时间复杂度：O(1)

队列

• 就像隧道，通过隧道的车辆只能从一边出、一边入，并且先驶入的先出来，不能“超车”，也不能“逆行”
• 可以用数组或者链表实现
• 入队（enqueue）：只允许在队尾位置放入元素
• 出队（dequeue）：只允许在队头一侧移除元素
• 循环队列：使数组形式存在的队列，在不断的出队入队中维持队列容量的恒定；具体操作：当队列满的时候，队尾指针指向数组的首位，直到（队尾指针+1）%数组长度 = 队头下标表示队列真的存满了

散列表（哈希表）

• 存在 键-值的映射关系（Key-Vaule），时间复杂度接近于O(1)
• 本质上也是数组，通过哈希函数将Key转换成对应的下标
• 通过 开放寻址法 和链表法来解决哈希冲突

写操作

• 通过哈希函数将key值转换为下标
• 如果下标无元素，则将元素填充到该下标；如果该下标下已经有元素了（哈希冲突），则使用开发寻址法（寻找下一个空档位置）或者链表法（将原元素的next下标指向要添加的元素）

写操作

• 通过哈希函数，将key转化为数组下标
• 通过这个下标找到对应的元素，再通过链表一个个比对key值是否相等

扩容

• 创建一个长度为原数组两倍的新的空数组
• 遍历所有元素，重新Hash后，添加到新数组中

应用

• 栈的应用：递归、回溯历史（回退栈）
• 队列的应用：对历史的“回放”

例如在多线程中，争夺公平锁的等待队列，就是按照访问顺序来决定线程在队列中的
次序的。

• 双端队列：可以在队头的一端入队或出队，也可以从队尾的一端入队或出队
• 优先队列：优先级高的节点先出队
• 散列表代表：HashMap

树

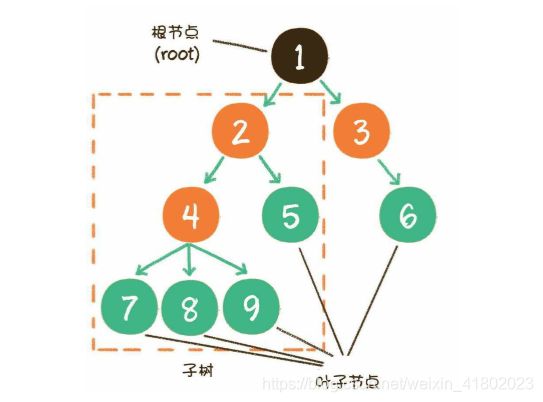
1. 有且仅有一个特定的称为根的节点。
2. 当n>1时，其余节点可分为m（m>0）个互不相交的有限集，每一个集合本身又是一 个树，并称为根的子树

• 节点1是根节点（root）,节点5、6、7、8是树的末端，没有“孩子”，被 称为叶子节点（leaf）。图中的虚线部分，是根节点1的其中一个子树。
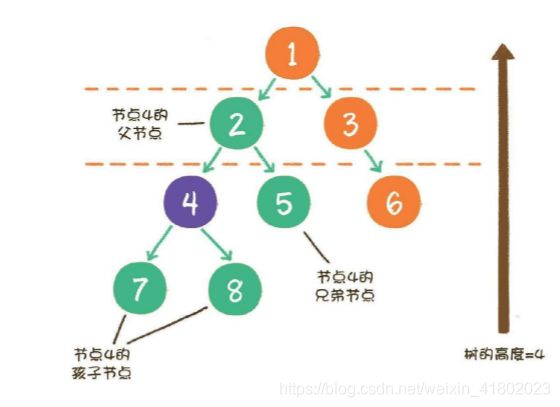
• 节点4的上一级节点，是节点4的父节点（parent）；从节点4衍生出来的 节点，是节点4的孩子节点（child）；和节点4同级，由同一个父节点衍生出来的节点， 是节点4的兄弟节点（sibling）
• 树的最大层级数，被称为树的高度或深度。显然，上图这个树的高度是4。

二叉树

• 是树的一种特殊的形式
• 每个节点最多（0、1、2）有两个子节点（左孩子、右孩子）
• 满二叉树定义：一个二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上， 那么这个树就是满二叉树
• 完全二叉树：对一个有n个节点的二叉树，按层级顺序编号，则所有节点的编号为从1到n。如果这 个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同，则这个二叉树为完 全二叉树。

满二叉树和完全二叉树的区别：满二叉树要求所有分支都是满的；而完全 二叉树只需保证最后一个节点之前的节点都齐全即可

链表实现

• 存储数据的data变量
• 指向左孩子的left指针
• 指向右孩子的right指针

数组实现

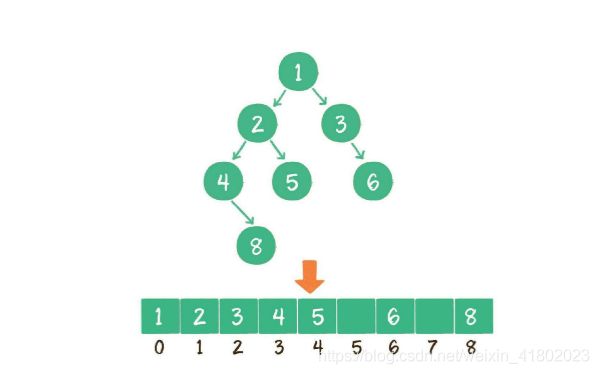
当子孩子没有数据时数组相应的位置会空出来，可以方便计算节点位置

• 当一个父节点下标是parent，则左孩子下标为：2 * parent + 1；右孩子下标为：2 * parent + 2
• 如果一个左孩子的下标是leftChild，则父节点下标位 （leftChild - 1）/ 2

应用

• 二叉查找树
• 也叫二叉排序树，特点：

• 如果左子树不为空，则左子树上所有节点的值均小于根节点的值
• 如果右子树不为空，则右子树上所有节点的值均大于根节点的值
• 左、右子树也都是二叉查找树
  自平衡：
  特殊情况下，会导致“失衡”，解决方法：自平衡（红黑树、AVL树、树堆）

二叉树的遍历

• 前序遍历：输出顺序 根节点 -> 左子树 -> 右子树
• 中序遍历：输出顺序 左子树 -> 根节点-> 右子树
• 后序遍历：输出顺序 左子树 -> 右子树 -> 根节点
• 层序遍历（广度优先遍历，一层层遍历）

 /**
     * 按前序遍历的顺序构建二叉树
     * @param inputList
     * @return
     */
    public static TreeNode createBinaryTree(LinkedList<Integer> inputList){

        if (inputList == null || inputList.isEmpty()) return null;

        TreeNode node = null;
        Integer data = inputList.removeFirst();
        if (data != null){
            node = new TreeNode(data);
            node.leftNode = createBinaryTree(inputList);
            node.rightNode = createBinaryTree(inputList);
        }


        return node;

    }

    /**
     * 二叉树的前序遍历
     * @param node
     */
    public static void preOrderTraveral(TreeNode node){

        if (node == null) return;

        System.out.print(node.data);
        preOrderTraveral(node.leftNode);
        preOrderTraveral(node.rightNode);

    }

    /**
     * 二叉树的中序遍历
     * @param node
     */
    public static void inOrderTraveral(TreeNode node){
        if (node == null) return;

        inOrderTraveral(node.leftNode);
        System.out.print(node.data);
        inOrderTraveral(node.rightNode);
    }

    /**
     * 二叉树的后序遍历
     * @param node
     */
    public static void postOrderTraveral(TreeNode node){
        if (node == null) return;

        postOrderTraveral(node.leftNode);
        postOrderTraveral(node.rightNode);
        System.out.print(node.data);
    }

二叉堆

本质上是一种完全二叉树，有两种类型：1. 最大堆 2.最小堆
最大堆：任何一个父节点的值，都大于或等于它左、右孩子节点 的值。
最小堆：的任何一个父节点的值，都小于或等于它左、右孩子节点的值。
两类操作：“上浮”和下沉
操作：

• 删除：是单一节点的下沉，时间复杂度O(logn)
• 插入：是单一节点的上浮，时间复杂度O(logn)
• 构建：需要所有非叶子节点依次下沉，时间复杂度O(n)

应用：

• 实现优先队列
• 堆排序

     /**
     * 堆的上浮操作
     * @param array 插入新数据后未调整的堆
     */
    public static void upAdjust(int[] array){
        int childIndex = array.length - 1;
        int parentIndex = (childIndex - 1)/2; // 找到父节点

        int temp = array[childIndex]; // temp 保存插入的叶子节点值，用于最后的赋值

        while (childIndex > 0 && temp < array[parentIndex]){
            array[childIndex] = array[parentIndex];
            childIndex = parentIndex;
            parentIndex = (childIndex - 1)/2;
        }

        array[childIndex] = temp;

    }


    /**
     * 堆的下沉操作
     * @param array 待调整的堆
     * @param parentIndex 要“下沉”的父节点
     * @param length 堆的有效长度
     */
    public static void downAdjust(int[] array,int parentIndex,int length){

        int temp = array[parentIndex];
        int childIndex = 2 * parentIndex + 1; // 找到左孩子

        while (childIndex < length){

            // 如果存在右孩子，且右孩子比左孩子小，将指针指向右孩子
            if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]){
                childIndex++;
            }

            // 如果父节点小于两个子孩子的值，则跳出
            if (temp < array[childIndex]) break;

            array[parentIndex] = array[childIndex];
            parentIndex = childIndex;
            childIndex = 2 * parentIndex + 1;

        }

        array[parentIndex] = temp;
    }


    public static void buildHeap(int[] array){

        // 从最后一个非叶子节点开始，依次做“下沉”调整
        for (int i = (array.length - 2)/2;i >= 0;i--){
            downAdjust(array,i,array.length);
        }

    }

二叉堆的应用：优先队列

队列遵循先进先出（FIFO）原则，优先队列不再遵循先进先出的原则，而是分为两种情况：

• 最大优先队列，无论入队顺序如何，都是当前最大的元素优先出队
• 最小优先队列，无论入队顺序如何，都是当前最小的元素优先出

特性：
入队：在数组末插入新节点，让新节点“上浮”到合适的位置，时间复杂度：O（logn）
出队：将堆顶的元素出栈，再将最后一个元素移到对顶，再进行“下沉”操作，时间复杂度：O（logn）

  private int[] array;
    private int size; // 当前队列大小


    public PriorityQueue() {

        // 初始长度为 32
        array = new int[32];

    }


    /**
     * 入队
     * @param val
     */
    public void enqueue(int val){
        if (size > array.length) resize();

        array[size++] = val;
        HeapHelper.upAdjust(array,size); // 上浮调整，传入有效长度
    }

    /**
     * 出队
     * @return
     * @throws Exception
     */
    public int dequeue() throws Exception {
        if (size <= 0) throw new Exception("no more data");
        int head = array[0];
        array[0] = array[--size];
        HeapHelper.downAdjust(array,0,size);// 0：要下沉的节点，这里是第一个，size：有效长度
        return head;

    }

树知识点小节

这里直接搬书里的

• 什么是树
  树是n个节点的有限集，有且仅有一个特定的称为根的节点。当n>1时，其余节点可 分为m个互不相交的有限集，每一个集合本身又是一个树，并称为根的子树。
• 什么是二叉树
  二叉树是树的一种特殊形式，每一个节点最多有两个孩子节点。二叉树包含完全二叉 树和满二叉树两种特殊形式。
• 二叉树的遍历方式有几种
  根据遍历节点之间的关系，可以分为前序遍历、中序遍历、后序遍历、层序遍历这4 种方式；从更宏观的角度划分，可以划分为深度优先遍历和广度优先遍历两大类。
• 什么是二叉堆
  二叉堆是一种特殊的完全二叉树，分为最大堆和最小堆。
  在最大堆中，任何一个父节点的值，都大于或等于它左、右孩子节点的值。
  在最小堆中，任何一个父节点的值，都小于或等于它左、右孩子节点的值。
• 什么是优先队列
  优先队列分为最大优先队列和最小优先队列。
  在最大优先队列中，无论入队顺序如何，当前最大的元素都会优先出队，这是基于最 大堆实现的。
  在最小优先队列中，无论入队顺序如何，当前最小的元素都会优先出队，这是基于最 小堆实现的。