【读书笔记】《王道论坛计算机考研机试指南》第六章

第六章 搜索

枚举

枚举是最简单也是最直白的搜索方式，它依次尝试搜索空间中所有的解，测试其是否符合条件，若符合则输出答案，否则继续测试下一组解。
但是在使用枚举这种相对较为暴力的算法来进行解题时， 我们对其时间复杂度要做特别的关注。枚举问题的时间复杂度往往与需要枚举的情况个数有关，因为我们必须不遗不漏的枚举每一种可能成为答案的情况。所以搜索空间越大，枚举的时间复杂度就越高。所以，我们在对某一问题进行枚举时，必须保证其时间复杂度在题目时限可以接受的范围内。

该例就是非常适合枚举的一例考研机试真题。首先，它需要枚举的情况十分简单，只需简单的枚举x, y的值即可，而z可由100-x-y的值得到。其次，它的枚举量仅有100*100数量级，在题目给定的时间范围内可以枚举完毕。所以，对于此类枚举情况不多，非常适合枚举的考题，无需再去考虑另外更具技巧的解法，毫不犹豫的暴力即可。

#include
int main(){
	int n;
	while(scanf("%d",&n) != EOF) {
		for(int x=0;x<=100;x++) { //枚举x的值
			for(int y=0;y<=100-x;y++){//枚举y的值，注意它们的和不可能超过100
				int z=100-x-y; //计算z的值
				if(x*5*3+y*3*3+z<=n*3){//考虑到一只小小鸡的价格为1/3,为避免除法带来的精度损失，这里采用了对不等式两端所有数字都乘3的操作，这也是避免除法的常用技巧
					printf("x=%d,y=%d,z=%d\n",x,y,z); //输出
				}
			}
		}
	}
	return 0;
}

我们回顾第二章讨论过的查找的几个要素：

1. 查找空间。在枚举问题中，所有可能成为答案的解组成了其查找空间。枚举过程即枚举查找空间中的每一个解。在枚举过程中，要做到不遺漏，不重复。
2. 查找目标。即查找到一组符合问题要求的解。为此，我们必须对枚举出来的每一个解进行相关判定。
3. 查找方式。与之前所讨论的查找方式相比,枚举的查找方式依旧比较原始，它简单的依次遍历所有的解，直到得到符合要求的解。

广度优先搜索(BFS)

Problem 1


所谓广度优先搜索,即在遍历解答树时使每次状态转移时扩展出尽可能多的新状态，并且按照各个状态出现的先后顺序依次扩展它们。其在解答树上的表现为对解答树的层次遍历，先由根结点扩展出所有深度为1的结点，再由每一个深度为1的结点扩展出所有深度为2的结点，依次类推，且先被扩展的结点其深度不大于后被扩展的结点深度。在这里，深度与所需的行走时间等价。这样,当搜索过程第一次查找到状态中坐标为终点的结点，其记录的时间即为所需最短时间。
但是，即便这样所需查找的状态还是非常得多，最坏情况下，因为每个结点都能扩展出六个新结点，那么仅走了10步，其状态数就会达到6的十次方，需要大量的时间才能依次遍历完这些状态。那么，我们必须采取相应的措施来制约状态的无限扩展。这个措施被称为剪枝。
首先，使用如下结构体保存每一个状态：

struct N {
	int x,y,z; //位置坐标
	int t; //所需时间
};

其次，为了实现各个状态按照其被查找到的顺序依次转移扩展，我们需要使用一个队列。即将每次扩展得到的新状态放入队列中,待排在其之前的状态都被扩展完成后，该状态才能得到扩展。
最后，为了防止对无效状态的搜索，我们需要一个标记数组mark[x][y][z],当已经得到过包含坐标(x, y, z)的状态后，即把mark[x][y][z]置为true，当下次再由某状态扩展出包含该坐标的状态时，则直接丢弃，不对其进行任何处理。
在明确了以上三点后，我们给出该题代码。

#include 
#include 
using namespace std;
bool mark[50][50][50]; //标记数组
int maze[50][50][50]; //保存立方体信息
struct N { //状态结构体
	int x,y,z;
	int t;
};
queue<N> Q; //队列，队列中的元素为状态
int go[][3]={ /*坐标变换数组，由坐标(x,y,z)扩展得到的新坐标均可通过
(x+go[i][0]，y+go[i][1], Z+go[i][2])得到*/
1,0,0,
-1,0,0,
0,1,0,
0,-1,0,
0,0,1,
0,0,-1
};
int BFS(int a,int b,int c) { //广度优先搜索，返回其最少耗时
	while(Q.empty()==false) { //当队列中仍有元素可以扩展时循环
		N now=Q.front(); //得到队头状态
		Q.pop(); //从队列中弹出队头状态
		for(int i=0;i<6;i++){//依次扩展其六个相邻节点
			int nx=now.x + go[i][0];
			int ny=now.y + go[i][1];
			int nz=now.z + go[i][2]; //计算新坐标
			if(nx<0||nx>=a||ny<0||ny>=b||nz<0||nz>=c)
			continue; //若新坐标在立方体外，则丢弃该坐标
			if (maze[nx][ny][nz]==1) continue; //若该位置为墙，则丢弃该坐标
			if (mark[nx][ny][nz]==true) continue; //若包含该坐标的状态已经被得到过，则丢弃该状态
			N tmp; //新的状态
			tmp.x=nx;
			tmp.y=ny;
			tmp.z=nz; //新状态 包含的坐标
			tmp.t=now.t+1; //新状态的耗时
			Q.push(tmp); //将该状态放入队列
			mark[nx][ny][nz]=true; //标记该坐标
			if(nx=a-1&&ny=b-1&&nz=c-1) return tmp.t;
			//若该坐标即为终点，可直接返回其耗时
		}
	}
	return -1;
}
int main(){
	int T;
	scanf("%d",&T); 
	while(T--) {
		int a,b,c,t;
		scanf("%d%d%d%d",&a,&b,&c,&t);
		for(int i=0;i<a;i++){
			for(int j=0;j<b;j++){
				for(int k=0;k<c;k++){
					scanf("%d",&maze[i][j][k]); //输入立方体信息
					mark[i][j][k]=false; //初始化标记数组
				}
			}
		}
		while(Q.empty()==false) Q.pop(); //清空队列
		mark[0][0][0]==true; //标记起点
		N tmp;
		tmp.t=tmp.y=tmp.x=tmp.z=0; //初始状态
		Q.push(tmp); //将初始状态放入队列
		int rec=BFS(a,b,c); //广度优先搜索
		if (rec <= t) printf("%d\n",rec); //若所需时间符合条件，则输出
		else printf("-1\n"); //否则输出-1
	}
	return 0;
}

我们通过状态之间的相互扩展完成在所有状态集合中的搜索，并查找我们需要的状态。利用这种手段,我们将原本对路径的搜索转化到了对状态的搜索上来。广度优先搜索即对由状态间的相互转移构成的解答树进行的按层次遍历。

Problem 2

与Problem 1一样，我们使用四元组(x, y, z, t)来表示一个状态，其中x、y、z分别表示三个瓶子中的可乐体积，t表示从初始状态到该状态所需的杯子间互相倾倒的次数。状态间的相互扩展，就是任意四元组经过瓶子间的相互倾倒而得到若干组新的四元组的过程。这样，当平分的状态第一次被搜索出来以后，其状态中表示的杯子倾倒次数即是所求。
同样的， 由于要搜索的是最少倒杯子次数，若四元组(x,y,z,t)中t并不是得到体积组x、y、z的最少倒杯子次数，那么该状态为无效状态，我们将其舍弃。其原因与第一例中一致，在程序中的实现方法也与第一例中一致。

#include 
#include 
using namespace std;
struct N { //状态结构体
	int a,b,c;//每个杯子中可乐的体积
	int t; //得到该体积组倾倒次数
};
queue<N> Q; //队列 
bool mark[101][101][101]; /*对体积组(x, y, z)进行标记，即只有第一次得到包
含体积组(x, y, z)的状态为有效状态，其余的舍去*/
void AtoB(int &a,int sa,int &b,int sb) { 
	/*倾倒函数，由容积为sa的杯子倒往容积为sb的杯子，其中引用参数a和b,初始时
	为原始杯子中可乐的体积，当函数调用完毕后，为各自杯中可乐的新体积*/
	if(sb-b>=a){//若a可以全部倒到b中
		b+=a;
		a=0;
	}
	else { //否则 
		a-=sb-b;
		b=sb;
	}
}
int BFS(int s,int n,int m) {
	while(Q.empty()==false) { //当队列非空时，重复循环
		N now=Q.front(); //拿出队头状态
		Q.pop(); //弹出队头状态
		int a,b,c;//a.b.c临时保存三个杯子中可乐体积
		a=now.a;
		b=now.b;
		c=now.c; //读出该状态三个杯子中可乐体积
		AtoB(a,s,b,n);//由a倾倒向b
		if (mark[a][b][c] == false) { //若该体积组尚未出现
			mark[a][b][c]=true; //标记该体积组
			N tmp;
			tmp.a=a;
			tmp.b=b;
			tmp.c=c;
			tmp.t=now.t + 1; //生成新的状态
			if(a==s/2&&b==s/2) return tmp.t;
			if(c==s/2&&b==s/2) return tmp.t;
			if(a==s/2&&c==s/2) return tmp.t; //若该状态已经为平分状态，则直接返回该状态的耗时
			Q.push(tmp); //否则放入队列
		}
		a=now.a;
		b=now.b;
		c=now.c; //重置a. b. c为未倾倒前的体积
		AtoB(b,n,a,s);//由b倾倒向a
		if (mark[a][b][c] == false) { //若该体积组尚未出现
			mark[a][b][c]=true; //标 记该体积组
			N tmp;
			tmp.a=a;
			tmp.b=b;
			tmp.c=c;
			tmp.t=now.t + 1; //生成新的状态
			if(a==s/2&b==s/2) return tmp.t;
			if(c==s/2&b==s/2) return tmp.t;
			if(a==s/2&&c==s/2) return tmp.t; //若该状态已经为平分状态，则直接返回该状态的耗时
			Q.push(tmp); //否则放入队列
		}
		a=now.a;
		b=now.b;
		c=now.c;
		AtoB(a,s,c,m);//由a倾倒向c
		if (mark[a][b][c] == false) { 
			mark[a][b][c]=true; 
			N tmp;
			tmp.a=a;
			tmp.b=b;
			tmp.c=c;
			tmp.t=now.t + 1; //生成新的状态
			if(a==s/2&b==s/2) return tmp.t;
			if(c==s/2&b==s/2) return tmp.t;
			if(a==s/2&&c==s/2) return tmp.t; //若该状态已经为平分状态，则直接返回该状态的耗时
			Q.push(tmp); //否则放入队列
		}
		a=now.a;
		b=now.b;
		c=now.c;
		AtoB(c,m,a,s);//由c倾倒向a
		if (mark[a][b][c] == false) { 
			mark[a][b][c]=true; 
			N tmp;
			tmp.a=a;
			tmp.b=b;
			tmp.c=c;
			tmp.t=now.t + 1; 
			if(a==s/2&b==s/2) return tmp.t;
			if(c==s/2&b==s/2) return tmp.t;
			if(a==s/2&&c==s/2) return tmp.t; 
			Q.push(tmp); 
		}
		a=now.a;
		b=now.b;
		c=now.c;
		AtoB(b,n,c,m);//由b倾倒向c
		if (mark[a][b][c] == false) { 
			mark[a][b][c]=true; 
			N tmp;
			tmp.a=a;
			tmp.b=b;
			tmp.c=c;
			tmp.t=now.t + 1; 
			if(a==s/2&b==s/2) return tmp.t;
			if(c==s/2&b==s/2) return tmp.t;
			if(a==s/2&&c==s/2) return tmp.t; 
			Q.push(tmp); 
		}
		a=now.a;
		b=now.b;
		c=now.c;
		AtoB(c,m,b,n);//由c倾倒向b
		if (mark[a][b][c] == false) { 
			mark[a][b][c]=true; 
			N tmp;
			tmp.a=a;
			tmp.b=b;
			tmp.c=c;
			tmp.t=now.t + 1; 
			if(a==s/2&b==s/2) return tmp.t;
			if(c==s/2&b==s/2) return tmp.t;
			if(a==s/2&&c==s/2) return tmp.t; 
			Q.push(tmp); 
		}
	}
	return -1;
}
int main(){
	int s,n,m;
	while (scanf("%d%d%d",&s,&n,&m) !=EOF) {
		if(s==0) break; //若s为0,则n,m为0则退出
		if(s%2==1){//若s为奇数则不可能平分，直接输出NO
			puts("NO"); 
			continue;
		}
		for(int i=0;i<=s;i++){
			for(int j=0;j<=n;j++){
				for(int k=0;k<=m;k++){
					mark[i][j][k]=false;
				}
			}
		} //初始化状态
		N tmp;
		tmp.a=s;
		tmp.b=0;
		tmp.c=0;
		tmp.t=0; //初始时状态
		while(Q.empty()==false) Q.pop(); //清空队列中状态
		Q.push(tmp); //将初始状态放入队列
		mark[s][0][0]=true; //标记 初始状态
		int rec=BFS(s,n,m); //广度优先搜索
		if (rec==-1) //若为-1输出NO
			puts("NO");
		else printf("%d\n",rec); //否则输出答案
	}
	return 0;
}

最后，我们总结广度优先搜索的几个关键字:

1. 状态。我们确定求解问题中的状态。通过状态的转移扩展，查找遍历所有状态，从而从中寻找我们需要的答案。
2. 状态扩展方式。在广度优先搜索中，我们总是尽可能扩展状态，并先扩展得出的状态先进行下一次扩展。在解答树上的变现为，我们按层次遍历所有状态。
3. 有效状态。对有些状态我们并不对其进行再一次扩展，而是直接舍弃它。因为根据问题分析可知，目标状态不会由这些状态经过若干次扩展得到。即目标状态，不可能存在其在解答树上的子树上，所以直接舍弃。
4. 队列。为了实现先得出的状态先进行扩展，我们使用队列，将得到的状态依次放入队尾，每次取队头元素进行扩展。
5. 标记。为了判断哪些状态是有效的，哪些是无效的我们往往使用标记。
6. 有效状态数。问题中的有效状态数与算法的时间复杂度同数量级，所以在进行搜索之前必须估算其是否在我们所可以接受的范围内。
7. 最优。广度优先搜索常被用来解决最优值问题，因为其搜索到的状态总是按照某个关键字递增(如前例中的时间和倒杯子次数)，这个特性非常适合求解最优值问题。所以一旦问题中出现最少、最短、最优等关键字，我们就要考虑是否是广度优先搜索。

递归

递归是一种十分常用的编码技巧，所谓即递归即函数调用函数本身，调用的方式按照问题的不同人为定义，这种调用方式被称为递归方式。同时，为了不使这样的递归无限的发生，我们必须设定递归的出口，即当函数到达某种条件时停止递归。如下求n阶层的递归程序：

int F(int x) {
if (x==0) return 1;
else return x*F(x-1);

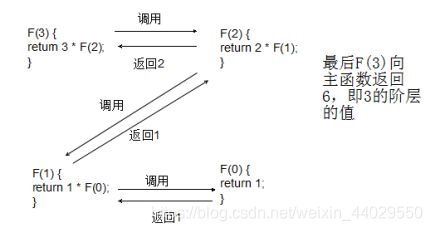
递归方式和递归出口是递归函数两个重要的要素，只要明确了这两个要素，那么递归函数就比较容易编写了。

与原始的汉诺塔问题不同，这里对圆盘的移动做了更多的限制，即每次只允许将圆盘移动到中间柱子上或者从中间柱子上移出，而不允许由第一根柱子直接移动圆盘到第三根柱子。
在这种情况下，我们考虑K个圆盘的移动情况。为了首先将初始时最底下、最大的圆盘移动到第三根柱子上,我们首先需要将其上的K-1个圆盘移动到第三根柱子上，而这恰好等价于移动K-1个圆盘从第一根柱子到第三根柱子。当这一移动完成以后，第一根柱子仅剩余最大的圆盘,第二根柱子为空，第三根柱子按顺序摆放着K-1个圆盘。我们将最大的圆盘移动到此时没有任何圆盘的第二根柱子上，并再次将K-1个圆盘从第三根柱子移动到第二根柱子,此时仍然需要移动K-1个圆盘从第一根柱子到第三根柱子所需的移动次数(第一根柱子和第三根柱子等价)，当这一移动完成以后将最大的圆盘移动到第三根柱子上，最后将K-1个圆盘从第一根柱子移动到第三根柱子上。若移动K个圆盘从第一根柱子到第三根柱子需要F[K]次移动,那么综上所述F[K]的组成方式为，先移动K-1个圆盘到第三根柱子需要F[K-1]次移动， 再将最大的圆盘移动到中间柱子需要1次移动，然后将K-1个圆盘移动回第一根柱子同样需要F[K-1]次移动，移动最大的盘子到第三根柱子需要1次移动，最后将K-1个圆盘也移动到第三根圖盘需要F[K-1]次移动，这样F[K]=3 * F[K-1]+2。即从第一根柱子移动K个圆盘到第三根柱子，需要三次从第一根柱子移动K-1个圆盘到第三根柱子,外加三次对最大圆盘的移动。若函数F(x)返回移动x根子所需要的移动次数，那么其递归方式为3 * F(x-1)+2。
同时我们要确定递归的出口。当x为1时，即移动一个盘子从第一根柱子移动到第三根柱子，其所需的移动次数是显面易见的，为2。即当函数的参数为1时直接返回2。

#include 
#include 
long long F(int num) { //递归函数，返回值较大使用long long类型
	if (num==1) return 2; //当参数为1时直接返回2
	else
		return 3*F(num-1)+2; //否则递归调用F(num-1)
}
int main() {
	int n;
	while (scanf("%d",&n) !=EOF) { 
		printf("%lld\n", F(n));
	}
	return 0;
}

递归的应用

Problem 1


题目大意为由给定的1到n数字中，将数字依次填入环中，使得环中任意两个相邻的数字间的和为素数。对于给定的n；按字典序由小到大输出所有符合条件的解(第一个数恒定为1)。这就是有名的素数环问题。
为了解决该问题，我们可以采用回溯法枚举每一个值。当第一个数位为1确定时，我们尝试放入第二个数，使其和1的和为素数，放入后再尝试放入第三个数，使其与第二个数的和为素数，直到所有的数全部被放入环中，且最后一个数与1的和也是素数，那么这个方案即为答案，输出；若在尝试放数的过程中，发现当前位置无论放置任何之前未被使用的数均不可能满足条件，那么我们回溯改变其上一个数，直到产生我们所需要的答案，或者确实不再存在更多的解。
为了实现这一回溯枚举的过程，我们采用递归的形式：

#include
#include
int ans[22]; //保存环中每一个被放入的数
bool hash[22]; //标记之前已经被放入环中的数
int n;
int prime[]={2,3,5,7,11,13,17,19,23,29,31,37,41}; 
/*素数，若需判断一个数是否为素数则在其之中查找，因为输入不大于16，
故两数和构成的素数必在该数组内*/
bool judge(int x){ //判断一个数是否为素数
	for(int i=0;i<13;i++){
		if(prime[i]==x) return true; //在素数数组中查找，若查找成功则该数为素数
	}
	return false; //否则不是素数
}
void check(){ //检查输出由回溯法枚举得到的解
	if(judge(ans[n]+ans[1])==false) return; //判断最后一个数与第一个数的和是否为素数，若不是则直接返回
	for(int i=1;i<=n;i++){ //输出解，注意最后一个数字后没有空格
		if(i!=1) printf(" ");
		printf("%d",ans[i]);
	}
	printf("\n");
}
void DFS(int num){ //递归枚举，num为当前已经放入环中的数字
	if(num > 1) //当放入的数字大于一个时
		if(judge(ans[num]+ans[num-1])==false) return;
		//判断最后两个数字的和是否为素数，若不是则返回继续枚举第num个数
	if(num==n){ //若已经放入了n个数
		check(); //检查输出
		return; //返回，继续枚举下一组解
	}
	for(int i=2;i<=n;i++){ //放入一个数
		if(hash[i]==false){ //若i还没有被放入环中
			hash[i]=true; //标记i为已经使用
			ans[num+1]=i; //将这个数字放入ans数组中
			DFS(num+1); //继续尝试放入下一个数
			hash[i]=false; // 当回溯回枚举该位数字时，将i重新标记为未使用
		}
	}
}
int main(){
	int cas=0; //记录Case数
	while(scanf("%d",&n)!=EOF){
		cas++; //Case数递增
		for(int i=0;i<22;i++) hash[i]=false; //初始化标记所有数字为未被使用
		ans[1]=1; //第一个数字恒定为1
		printf("Case %d: \n",cas); //输出Case数
		hash[1]=true; //标记1被使用
		DFS(1); //继续尝试放入下一个数字
		printf("\n");
	}
	return 0;
}

递归函数在另一个问题上也具有巨大的优势一一图的遍历。
Problem 2


我们可以这样解决这个问题，首先对图上所有位置均设置一个标记位，表示该位置是否已经被计算过，且该标记仅对地图上为@的点有效。这样我们按从左至右、从上往下的顺序依次遍历地图上所有位置，若遍历到@，且该点未被标记，则所有与其直接相邻、或者间接相邻的@点与其一起组成一个块，该块即为一个。
我们需要计算的块，将该块中所有的@位置标记为已经计算。这样，当所有的位置被遍历过后，我们即得到了所需的答案。

#include 
char maze[101][101]; //保存地图信息
bool mark[101][101]; //为图上每一个点设立一个状态
int n,m; //地图大小为n*m
int go[][2]={1,0,-1,0,0,1,0,-1,1,1,1,-1,-1,-1,-1,1}; //八个相邻点与当前位置的坐标差
void DFS(int x,int y) { //递归遍历所有与x，y直接或间接相邻的@
	for (int i=0;i<8;i++) { //遍历八个相邻点
		int nx=x+go[i][0];
		int ny=y+go[i][1]; //计算其坐标
		if(nx<1||nx>n||ny<1||ny>m)continue;//若该坐标在地图外
		if(maze[nx][ny]=='*') continue; //若该位置不是@
		if (mark[nx][ny]==true) continue; //若该位置已经被计算过
		mark[nx][ny]==true; //标记该位置为已经计算
		DFS(nx, ny); //递归查询与该相邻位置直接相邻的点
	}
	return;
}
int main(){
	while (scanf("%d%d",&n,&m) !=EOF) {
		if(n==0&&m==0)break;
		for(int i=1;i<=n;i++){
			scanf("%s",maze[i]+1); // 第i行地图信息保存在maze[i][1]到maze[i][m]中
		} //按行为单位输入地图信息
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				mark[i][j]=false;
			} 
		} //初始化所有位置为未被计算
		int ans=0; //初始化块计数器
		for(int i=1;i<=n;i++){
			for (int j=1;j<=m;j++) { //按顺序遍历图中所有位置
				if (mark[i][j]==true) continue; //若该位置已被处理，跳过
				if (maze[i][j]=='*') continue; //若该位置不为@，跳过
				DFS(i,j); //递 归遍历与其直接或间接相邻的@
				ans++; //答案递增
			}
		}
		printf("%d\n", ans); 
	}
	return 0;
}

在结束对递归的讨论之前，还需要特别的强调，使用递归函数务必注意递归的层数。一个程序可以使用的栈空间是有限的，当递归的过深或者每层递归所需的栈空间太大将会造成栈的溢出，使评判系统返回程序运行时异常终止的结果，一旦你的递归程序出现了这种错误，你就要考虑是否是由递归的太深而造成了爆栈。这是使用递归程序一个很重要的注意要点。具体可使用的栈大小，因个评判系统不同而有所差异，需要读者自行测试后确定。

深度优先搜索(DFS)

这里给出的深度优先遍历不使用堆栈而是使用递归程序。
由于其缺少了广度搜索中按层次递增顺序遍历的特性。所以当深度优先搜索搜索到我们需要的状态时，其不再具有某种最优的特性。所以，在使用深度优先搜索时，我们更多的求解有或者没有的问题，即对解答树是否有我们需要的答案进行判定，而一般不使用深度优先搜索求解最优解问题。


题目大意：有一个N*M的迷官，包括起点S,终点D,墙X,和地面，0秒时主人公从S出发，每秒能走到四个与其相邻的位置中的一个，且每个位置被行走之后都不能再次走入，问是否存在这样一条路径使主人公在T秒时刚好走到D。
在这个问题中，题面不再要求我们求解最优解，而是转而需要我们判定是否存在一条符合条件的路径，所以我们使用深度优先搜索来达到这个目的。确定状态三元组(x, y, t)，(x, y)为当前点坐标，t为从起点走到该点所需的时间。我们需要的目标状态为(dx,dy, T)，其中(dx,dy)为D所在点的坐标，T为所需的时间。初始状态为(sx,sy, 0)，其中(sx,sy)为S所在点的坐标。
同样的，在深度优先搜索中也需要剪枝，我们同样不去理睬被我们判定不可能存在所需状态的子树,以期能够减少所需遍历的状态个数,避免不必要的超时。
注意到，主人公每走一步时，其所在位置坐标中，只有一个坐标分量发生增一或者减一的改变，那么两个坐标分量和的奇偶性将发生变化。这样，当主人公走过奇数步时，其所在位置坐标和的奇偶性必与原始位置不同；而走过偶数步时，其坐标和的奇偶性与起点保持不变。若起点的坐标和的奇偶性和终点的坐标和不同，但是需要经过偶数秒使其刚好达到，显然的这是不可能的，于是我们直接判定这种情况下，整棵解答树中都不可能存在我们所需的状态，跳过搜索部分，直接输出NO。

#include 
char maze[8][8]; //保存地图信息
int n,m,t; //地图大小为n*m,从起点到终点能否恰好t秒
bool success; //是否找到所需状态标记
int go[][2]={1,0,-1,0,0,1,0,-1}; //四方向行走坐标差
void DFS(int x,int y,int time) { //递归形式的深度优先搜索
	for(int i=0;i<4;i++){//枚举四个相邻位置
		int nx=x+go[i][0];
		int ny=y+go[i][1]; //计算其坐标
		if(nx<1||nx>n||ny<1||ny>m) continue;//若坐标在地图外则跳过
		if (maze[nx][ny]=='X') continue; //若该位置为墙，跳过
		if (maze[nx][ny]=='D') { //若该位置为门
			if(time+1==t){//若所用时间恰好为t
				success=true; //搜索成功
				return; //返回
			}
			else continue; 
		//否则该状态的后续状态不可能为答案(经过的点不能再经过)。跳过
		}
		maze[nx][ny]='X'; //该状态扩展而来的后续状态中，该位置都不能被经过，直接修改该位置为墙
		DFS(nx, ny, time + 1); //递归扩展该状态，所用时间递增
		maze[nx][ny]='.'; /*若其后续状态全部遍历完毕，则退回上层状态，将因为要
		搜索其后续状态而改成墙的位置改回普通位置*/
		if(success) return; //假如已经成功，则直接返回，停止搜索
	}
}
int main() {
	while (scanf("%d%d%d", &n, &m, &t) !=EOF) {
		if(n==0&&m==0&&t==0)break;
		for(int i=1;i<=n;i++){
			scanf("%s",maze[i]+1);
		} 
		success=false; // 初始化成功标记
		int sx,sy;
		for(int i=1;i<=n;i++) { //寻找D的位置坐标
			for(int j=1;j<=m;j++){
				if(maze[i][j]=='D') {
					sx=i;
					sy=j;
				}
			}
		}
		for(int i=1;i<=n;i++) { //寻找初始状态
			for(int j=1;j<=m;j++){
				if (maze[i][j]=='S'&&(i+j)%2==((sx+sy)%2+t%2)%2){
				/*找到S点后，先判断S与D的奇偶性关系，是否和t符合，
				即符合上式，若不符合直接跳过搜索*/
					maze[i][j]='X'; //将起点标记为墙
					DFS(i,j,0); //递归扩展初始状态
				}
			}
		}
		puts(success==true ? "YES" : "NO"); //若success为真， 则输出yes
	}
	return 0;
}

如该代码所示，我们用递归函数完成深度优先搜索。深度优先搜索的各素如下：
搜索空间:广度优先搜索相同，依旧是所有的状态。
搜索目的:查找一个可以表示原问题解的状态。
搜索方法:在解答树上进行先序遍历。
总结深度优先搜索的相关特点：
其查找空间和查找目的均与广度优先搜索保持一致，与广度优先搜索有较大不同的是它的查找方式。深度优先搜索对状态的查找采用了立即扩展新得到的状态的方法，我们常使用递归函数来完成这一功能。正是由于采用这样的扩展方法，由它搜索而来的解不再拥有最优解的特性，所以我们常用它来判断解是否存在的存在性判定。