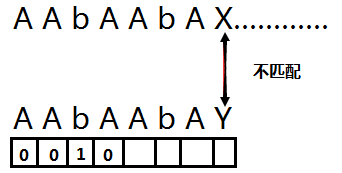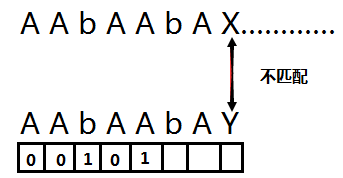(6)KMP算法(求子串的位置)______字符串的匹配

问题：

已知字符串 B 是字符串 A 的一个子串,问字符串 B 在字符串 A 的第一次出现位置. 

暴力方法:从 A 字符串 的每个位置开始对字符串 B 进行匹配. 这种方法根据数据的不同 复杂度不同最高可以达到 O( m*n ).   (m,n分别为两个字符串的长度)

KMP算法：  

我们先来看普通的暴力方法在对下面的匹配过程:

这个匹配过程到达 X,Y 处发现不匹配,按照暴力方法我们就把下面的字符串向右移动一个字符然后继续跟A进行匹配.但是实际上看图我们就可以知道移动一个字符肯定还是无法匹配成功, 而这样的一步一步的移动也是十分费时.那么我们就要找到最佳的右移长度.

看这幅图：

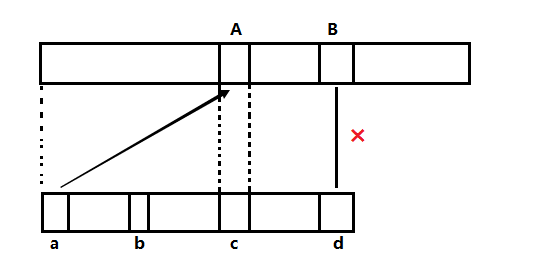假如在匹配d和b的时候失败了,我们移动 a 到 A  对应的位置 , 那么就要满足 AB 段和 ab段匹配 ,又因为 cd 和 AB 段已经匹配上了, 实际上就是要 ab 段和 cd 段匹配.我们要移动最长距离就要保证 ab  和 cd 在匹配上的同时, ab 串的长度最大值.那么就可以直接把 a 移动到 A 进行匹配.换句话就是求 下面那个字符串在 ad 段部分的首尾匹配子串的最大长度.

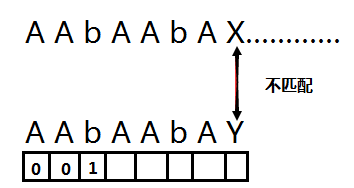
这个时候我们引入一个数组 c [ i ]  表示 下面的待匹配的子串在 0 ~ i-1 部分的首尾匹配子串的最大长度.初始化前面两个为0.

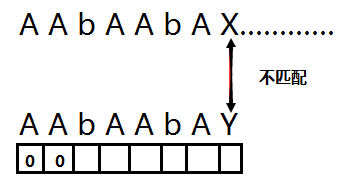然后上下开始匹配,匹配到 b 的时候我们先计算下面数组的值,计算方法是看前一个位置的数组的值,这里 b 的前面一个位置的值是0,那么就比较前一字符与0位置字符是否相等.如果相等,当前数组值就等于前一数组的值加1,如果不相等当前数组值就等于0.

现在我们就递推到b 发现  b 前面的字符和 0字符相同都为 A 那么  b 下面对应的数组的值为 0+1=1;

继续递推,到 A  ,前一数组的值 为 1 , 那么我们比较前一字符与 1 位置的字符 一个是 b ,一个是 A.那么 A对应下面的数组值为 0;

继续递推到 A ,前一数组的值为 0 , 那么我们比较前一字符与 0 位置的字符, 两个都是A 那么 当前A下面对应的数组值为0+1=1

继续匹配……

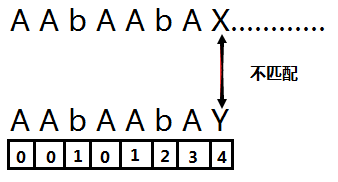
直到算完 Y 下面的数组的值后发现 上下不匹配, 我们找 Y下面的值 4, 然后从 4 号 位置的字符 与上面字符串的 X进行匹配,如果相同就继续重复以上操作.如果不相同那么继续调用4 号位置的字符下面的数组的值 0 ,然后用 0位置的元素和 X 比较.相同继续向后匹配,如果不同就继续调用下面的数组………………(注意:如果0

位置的字符也无法匹配 X 那么不用调用0号位置字符下面的数组的值,而是继续用0号位置的字符比较上面 X 后面的一个字符……)

结束:如果下面的字符串的最后一个字符也匹配成功那么, 上面字符串的匹配成功的最后一个字符位置减去下面字符串的长度再加1 就是下面字符串出现在上面字符串的第一次位置.

代码：

#include 
#include 
char str1[100],str2[10]; //str2是str1的子串.
int k,c[10],ans;
void kmp(int t1,int t2)
{
	if(str2[t2]=='\0'){           //先判断是否匹配完
		ans=t1-t2;
		return;
	}
	if(t2>1&&c[t2]==-1){         //继续计算当前字符下面的数组的值.
		if(str2[t2-1]==str2[c[t2-1]]) c[t2]=c[t2-1]+1;
		else c[t2]=0;
	}
	if(str1[t1]==str2[t2])      // 如果当前字符匹配成功,继续向后匹配.
		kmp(t1+1,t2+1);
	else if(t2==0)              // 如果当前字符匹配失败,但是下面的字符位置是0,那么上面字符向后移动一个继续匹配.
		kmp(t1+1,t2);
	else                       // 如果当前字符匹配失败,但是下面字符的位置不是0,那么调用当前字符下面c数组的值进行匹配
		kmp(t1,c[t2]);
}
int main()
{
	while(scanf("%s%s",str1,str2)!=EOF){
		memset(c,-1,sizeof(c));
		c[0]=c[1]=0;  //初始化c数组.
		kmp(0,0);
		printf("%d\n",ans+1);
	}
	return 0;
}

时间复杂度在 O(n)~O(n+m) 之间,  注意：n 为 str1 的长度