Codeforces Round #595 (Div. 3)
A. Yet Another Dividing into Teams
手速题
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
B. Books Exchange
其实问的就是每个环内的点的个数，岂不是带权并查集维护一下就可以了嘛。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
C. Good Numbers
一个被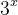
的和表示的数是一个good number，但是，每个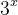不能超过一个。那么，我们可以去看二进制的表示，很容易发现，我们可以把一个数那三进制表示，但是有的位可能为2个，这时候就是去给前一位+1，然后对后面的所有直接赋值为0即可。
直接贪心。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
D. Too Many Segments
手玩一下，很容易发现，如果我们对左区间升序，然后去看右区间，这时候会发现，我们应该贪心的选择右端点最远到达的，并且左区间还得包含目前的这个点的，那么我们可以去搜索一下。
现在，D2，N很大，这时候我们肯定得要去优化一下暴力的解法，这里就可以用一下差分来降维了。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
E. By Elevator or Stairs?
DP，其实最短路也就可以了的。
二维DP，第二维的0表示直接走楼梯，第二维的1表示用了电梯，那么就是需要加上c了。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
F. Maximum Weight Subset
树形DP（好像有人用一些什么最大权值的独立集给过了，什么操作啊喂！QAQ？）
题目要找这样的集合，集合内的每个点对相互之间的距离都大于K，并且求其最大的权值。
其实也就是去求最大权值独立集。
怎么搞呢？我们可以去处理每个点的向下的间隔，譬如说，我们的间隔为0，是不是代表了我们把目前的这个点给取了，所以开一个二维dp[ i ][ j ]，其中i表示的是结点的序号，j表示的是间隔，于是乎有dp[u][0] = a[u];
画个图吧：
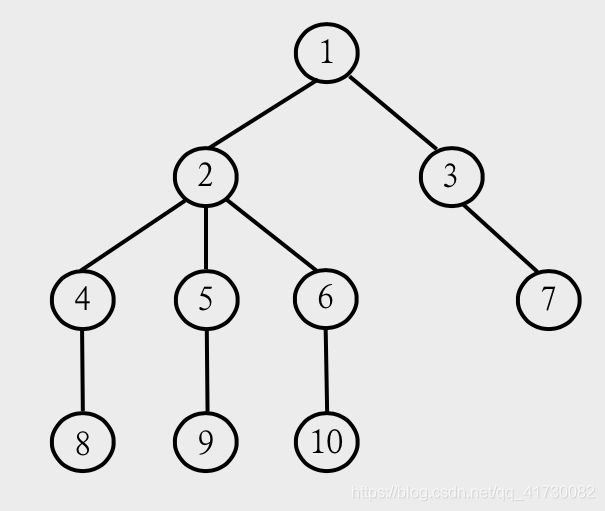
这时候，我们假设K为2，那么如果我取了1这个结点，是不是代表了是一定不可以取2、3两个结点的，然后以此类推。
换个角度来看这个问题，我们现在假如要去取1号点，就代表了dp[1][0] = a[1]; 那么，我们还可以怎样的去表示1这号结点的贡献呢？dp[1][1] = dp[1][1] + max(dp[3][0], dp[7][0])，这个等式可以化简一下，dp[1][1] = dp[1][1] + max(dp[3][0], dp[3][1])，这里，“dp[3][1]”就是等同于“dp[7][0]”，因为代表了不去取3这个结点的a[3]，而是改为取7号结点的a[7]。
所以嘛，在这里，如果我们访问到根为u的子树，dp[u][i]，以及子结点v，dp[v][j]，如果“i + j + 1 > K”就是说明这是我们可以取的结点了，这里的j是需要“+1”的，是因为深度要往上提1了。然后这时候就是去更新答案了。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
The End
Rating changes for the last round are temporarily rolled back. They will be returned soon.
难得要涨超级多的分的说，什么时候才给我还回来啊！！！
