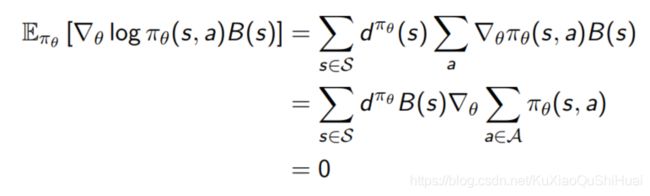强化学习笔记(6)Policy Gradient 策略梯度下降 DPG/MCPG/AC
文章目录
- 概念
- Value-Based and Policy-Based RL
- Value-Based
- Policy -Based
- Actor-Critic
- 目标函数的确定
- 梯度下降解决问题
- Likelihood ratios 自然对数
- Softmax Policy
- Gaussian Policy 连续动作空间
- 一步MDP过程为例:利用score function推导梯度。
- One Step MDPs的推广:策略梯度下降理论(Policy Gradient Theorem):
- 一些算法实现
- MCPG
- Actor-Critic
- 例子:Actor-Critic based on Action-Value critic
- Actor-Critic 算法的偏差
- Compatible function approximation Theorem.
- 使用Baseline 来减少A-C算法的波动(方差问题)
- 估计Advantage function
- Critics的参数更新
- Actor的参数更新
- Natural Policy Gradient (新的策略方法。不是上面所说的加入高斯噪音)
- Natural Actor-Critic
概念
之前都是基于价值函数或者状态行为价值对的。
在大规模问题时由于我们不可能存储每一个状态行为价值,所以我们使用Function来估计该状态的价值。我们通过训练从而精确function里面的参数。
这都是基于状态价值的。
如果对于行为action很多,或者行为是连续的。那么我们能否确定一个函数 P \mathbb P P,我们把状态s等参数输入进去,就能等得到一个行为a
π θ ( s , a ) = P [ a ∣ s , θ ] \pi_{\theta}(s,a) = \mathbb P[a | s,\theta] πθ(s,a)=P[a∣s,θ]
Value-Based and Policy-Based RL
Value-Based
- 学习的是Value Function.
- 使用很简单策略,比如对于基于Value的 ϵ − g r e e d y \epsilon -greedy ϵ−greedy
Policy -Based
- 不需要Value Function
- 我们要学习一个Policy函数,能够产生行为
Actor-Critic
两个都学
- 学习Value Function
- 学习Policy
优点:PG
-
更好的收敛性
-
高维度、连续动作空间更有效
-
能够学习==随机策略==
随机策略例子: 石头剪刀布的游戏。在随机生成动作的时候,你就可以更加了解对手的习惯。就是在选择动作的时候使用随机的,不是贪婪策略
缺点:
- 纯的策略学习,可能收敛到局部最优,不是全局最优
- 策略评估时通常不够高效,或者有高方差。
目标函数的确定
PG的目标: 给出一个policy π θ ( s , a ) \pi_\theta(s,a) πθ(s,a),所含参数为 θ \theta θ,找到一个最优的 θ \theta θ
问题: 如何衡量策略 π θ \pi_\theta πθ的好与坏?
现在的问题就变成了寻找 θ \theta θ,最大化 J ( θ ) J(\theta) J(θ)
一些方法:
梯度下降解决问题
Likelihood ratios 自然对数
这是一个定理:
假设 策略 π θ \pi_\theta πθ 是可微的, 那么他的梯度为 ∇ θ π θ ( s , a ) \nabla _\theta \pi_\theta(s,a) ∇θπθ(s,a)
∇ θ π θ ( s , a ) = π θ ( s , a ) ∇ θ π θ ( s , a ) π θ ( s , a ) = π θ ( s , a ) ∇ θ log π θ ( s , a ) \nabla _\theta \pi_\theta(s,a) = \pi_\theta(s,a) \frac{\nabla _\theta\pi_\theta(s,a)}{\pi_\theta(s,a)} \\ = \pi_\theta(s,a) \nabla _\theta \log \pi_\theta(s,a) ∇θπθ(s,a)=πθ(s,a)πθ(s,a)∇θπθ(s,a)=πθ(s,a)∇θlogπθ(s,a)
log是以e为底的,也就是ln
反过来就是一个复合求导
称 ∇ θ log π θ ( s , a ) \nabla _\theta \log \pi_\theta(s,a) ∇θlogπθ(s,a)为score function,他们告诉我们从哪个特殊的方向进行调整来获得较好的结果。
Softmax Policy
解决离散问题,,确定动作a
Gaussian Policy 连续动作空间
一步MDP过程为例:利用score function推导梯度。
One-Step 是指做出一个动作,就到了终止状态。所以没有序列。

One Step MDPs的推广:策略梯度下降理论(Policy Gradient Theorem):
-
使用likelihood ratio方法到多步的MDPs,就是策略梯度下降。
-
使用长期价值函数 Q π ( s , a ) Q^\pi (s,a) Qπ(s,a)来代替立得得奖励r
一些算法实现
上述提出了梯度下降理论,这个理论的一些实现方式:
MCPG
这里面的 v t v_t vt就是之前用的 G t G_t Gt,代表return。带衰减的奖励和。

Actor-Critic
- MCPG方法存在着高方差的问题。(不稳定,由于随机因素存在,模型表现时好时坏), A-C就是解决这个问题的。
放弃MCPG算法中使用return来评估策略好坏,而是指用一个critic函数来评价(比如critic可以是一个网络)
Actor和Critic同时提升更新参数。
Critic用来策略评估,就是上一篇所说的Policy Evaluation问题。
- Monte-Carlo policy evaluation
- Temporal-Difference learning
- TD( λ \lambda λ)
例子:Actor-Critic based on Action-Value critic
例子:
Actor-Critic 算法的偏差
近似的策略梯度引入了偏差。
一个由偏差的policy gradient有可能找不到正确的解。幸运的是如果我们谨慎的选择价值估计函数(value function approximation),我们就能够避免偏差。
那么如何找这个value function approximation?
Compatible function approximation Theorem.
证明过程
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-befZoUdN-1586684077045)(6_policy_gradient.assets/image-20200403162701988.png)]
使用Baseline 来减少A-C算法的波动(方差问题)
我们从策略梯度中减去一个baseline函数B(s), 这样做能够在不改变数学期望的情况下,减小方差。
一个号的baseline函数就是价值函数 B ( s ) = v π θ ( s ) B(s) = v^{\pi_\theta}(s) B(s)=vπθ(s)
之前的Q用A来代替:(Advantage function)
其中,对于B(s)那一项,也就是上式中 v π θ ( s ) v^{\pi_\theta}(s) vπθ(s).
不改变期望的证明:
估计Advantage function
方法一
- Advantange function 能够显著降低PG的方差(增强稳定性)
- 如果使用advantange function,critic就应该同时估计 V π θ ( s ) V^{\pi_\theta}(s) Vπθ(s)和 Q π θ ( s , a ) Q^{\pi_\theta}(s,a) Qπθ(s,a), 才能够产生A(s,a) = V(s)- Q(s,a)
- 更新的时候要同时更新V的参数和Q的参数。例如使用TD 算法。
使用TD error。 TD error 是Advantage function的无偏差估计。计算出来的梯度方向应该是相同的。

Critics的参数更新
Actor的参数更新
MC中的 v t v_t vt是return。
上面两个例子都是使用减去baseline的。
使用TD( λ \lambda λ )和效用迹理论更新
Natural Policy Gradient (新的策略方法。不是上面所说的加入高斯噪音)
Natural Actor-Critic
一种新的方法。