树形dp:选课

树形dp:选课

题目

Description

学校实行学分制。每门的必修课都有固定的学分，同时还必须获得相应的选修课程学分。学校开设了N（N<300）门的选修课程，每个学生可选课程的数量M是给定的。学生选修了这M门课并考核通过就能获得相应的学分。

在选修课程中，有些课程可以直接选修，有些课程需要一定的基础知识，必须在选了其它的一些课程的基础上才能选修。例如《Frontpage》必须在选修了《Windows操作基础》之后才能选修。我们称《Windows操作基础》是《Frontpage》的先修课。每门课的直接先修课最多只有一门。两门课也可能存在相同的先修课。每门课都有一个课号，依次为1，2，3，…。 例如:表中1是2的先修课，2是3、4的先修课。如果要选3，那么1和2都一定已被选修过。 　　

你的任务是为自己确定一个选课方案，使得你能得到的学分最多，并且必须满足先修课优先的原则。假定课程之间不存在时间上的冲突。
Input

输入文件的第一行包括两个整数N、M（中间用一个空格隔开）其中1≤N≤300,1≤M≤N。

以下N行每行代表一门课。课号依次为1，2，…，N。每行有两个数（用一个空格隔开），第一个数为这门课先修课的课号（若不存在先修课则该项为0），第二个数为这门课的学分。学分是不超过10的正整数。

Output

输出文件每行只有一个数。第一行是实际所选课程的学分总数。

Sample Input

7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2
Sample Output

13

题解:

虽然树形dp听上去高大上,但其实和正常的线性dp也差不多,只不过是在树上进行罢了.
而解树形dp题的重点还是在于dp的状态怎么定义和dp怎么转移

以选课这道题目为例题目中有的科目有先修课(即要先学完前一课,才能学这一课),而且每门课的直接先修课最多只有一门.这正好符合了树的概念,那么我们就可以很快想到根据科目之间的关系造出一棵多叉树

于是题目中的样例就有了如下的一棵多叉树:

之后我们就要思考有dp该定义什么状态

首先,将题目中的状态提炼出来:科目,该科目的先修课,该科目的分数,选了多少科目,选了的科目的总分数
先修课已经放在树里了,就不用考虑了.
科目的分数也显然不用考虑.
而dp的权值显然是总分数
那么dp的下标应该就是选到那个科目,和选了多少科目.
这样我们就将dp的状态就定义出来了:
dp[i][j]表示在i即i以下的子树上选j门课目所能得到的最大的分数

状态定义好了,我们就要思考dp该如何转移了

由上图可知一个节点可能有很多儿子,因此要将能选科目的数量分给自己的子树,
如果在i处能选j门学科,i的儿子有son[1],son[2]…son[k],在son[1]花的科目数为a1,son[2]的为a2…son[k]的为ak.
学i门课目的分数为val[i].
不取自己时a1+a2+..+ak=j;
dp[i][j]=Max{dp[i][j],dp[son[1][a1]+dp[son[2]][a2]+..dp[son[k][ak]}
取自己时a1+a2+…+ak=j-1;
dp[i][j]=Max{dp[i][j],dp[son[1][a1]+dp[son[2]][a2]+..dp[son[k][ak]+val[i]}
这样还要a1,a2..ak有许多中情况,这样进行转移显然太麻烦了.

因此我们要考虑怎样进行优化

给出如下优化:将一棵树的子树分为左儿子和右兄弟,再进行转移.
这样将科目分给子树时 只用考虑给左子树分多少科目,就可以知道给右子树分了多少科目,这样思路就明朗多了.
这样只要造出这样的一棵树就可以了.
按照优化的方法进行模拟即可:一个节点的第一个儿子当做左儿子,剩下的儿子当做上一个儿子的右兄弟.
这样就造出了如下的一棵树:

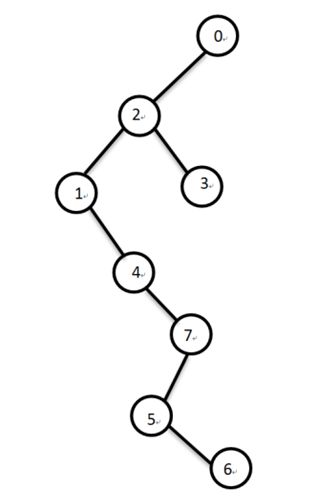
这样转移就简单多了:dp[i][j]=Max{dp[i][j],val[i]+dp[L[i]][k]+dp[R[i]][j-k-1]}(k∈[0,j-1])
dp[i][j]=Max{dp[L[i]][k]+dp[R[i]][j-k]}(k∈[0,j] )
//当没有左儿子或右兄弟是要分类讨论一下,在此就不做赘述了

代码如下:

#include
#include
#include
#include
#define M 305
using namespace std;
int val[M],res;
vector<int>G[M];
int n,m;
int L[M],R[M];//将多叉树转化成二叉树,左子树为儿子,右子树为兄弟 
void build(int x,int f){
    bool ff=0;
    int pre;
    for(int i=0;iint y=G[x][i];
        if(y==f)continue;
        if(ff){
            R[pre]=y;
            pre=y;
            build(y,x);
        }else{
            L[x]=G[x][i];
            build(y,x);
            ff=1;
            pre=G[x][i];
        }
    }
}
int dp[M][M];//dp[i][j]表示在i这棵子树上花费j时的最大价值 
int dfs(int x,int t){
    if(t<=0)return 0;
    if(dp[x][t])return dp[x][t];
    if(!L[x]){
        if(!R[x])return dp[x][t]=val[x];
        else return dp[x][t]=max(val[x]+dfs(R[x],t-1),dfs(R[x],t));
    }else{
        if(!R[x])return dp[x][t]=val[x]+dfs(L[x],t-1);//必须取自己,否则不能取自己的左儿子 
        else{
            int mx=0;
            for(int i=0;i//在自己身上花费1,在左子树上花费i的时间,即在右子树上花费t-i-1的时间 
                mx=max(mx,dfs(L[x],i)+dfs(R[x],t-i-1)+val[x]);
            }
            mx=max(mx,dfs(R[x],t));
            return dp[x][t]=mx;
        }
    }
}
int main(){
    scanf("%d %d",&n,&m);
    for(int i=1;i<=n;i++){
        int x;
        scanf("%d %d",&x,&val[i]);
        G[x].push_back(i);
        G[i].push_back(x);
    }
    build(0,-1);
    printf("%d\n",dfs(L[0],m));
    return 0;
}

总之,树形dp中有时可以将多叉树转化为(左儿子,右兄弟的)二叉树,这样往往能将问题简化,更好地写出递推式.^_^

Orz 小的不才,望主子能理解 Orz