DSM: Direct Sparse Mapping
Direct Sparse Mapping
Introduction
- 滑窗的会边缘化掉离开视场的点,同时来保证可观性的一致,不能重用边缘化的地图点
- 特征点法一般根据共视关系选固定位置的激活关键帧和地图点,通过固定一帧的策略保证可观性
- 选择以前的关键帧,结合时间和共视关系来选择激活的关键帧
- 时间上远的帧会受drift影响,因此使用多尺度优化,来增加收敛半径
- 由于距离远伪观测(外点)会增加,使用t分布来更鲁棒地处理
DSO和LDSO的缺点:
- 使用了不同的目标函数和点类型来完成里程计估计
- 闭环检测依赖于特征点的可重复性,损失一些可以用来矫正的点
- 闭环的误差较正均匀分布在关键帧上,这可能不是最优解
- 地图点的信息没有被reuse
Direct Mapping
- 跟踪线程以帧率速度输出位姿,会判断是否加入关键帧
- 建图线程处理新的帧,来跟踪关键帧上的点(候选点逆深度更新),插入关键帧会重新计算local window,激活新的点,优化motion和structure。然后为了保证全局一致,移除外点,检测遮挡,避免点的重复。
使用固定其它帧的方式来保证不可观自由度的一致性。
LMCW的初始解不在收敛半径内,所以使用粗到精的方式来优化,估计的几何作为下一层的初始值。
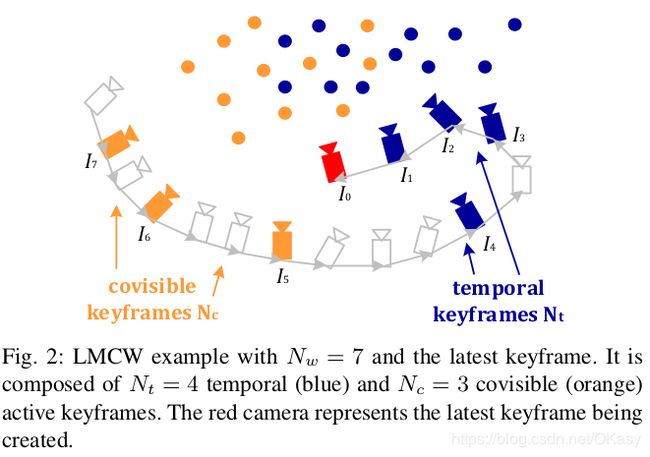
LMCW: Local Map Covisibility Window
由时间和共视策略组成,都是相对于最新关键帧的。
时间窗口主要目的是来优化新的点(初始化新点),并且保证里程计精度。
固定时间窗口的大小,从时间窗口移除关键帧的策略:
- 总是保留上两个关键帧( I 1 I_1 I1和 I 2 I_2 I2),这保证里程计在挑战环境下(如大旋转)也能保证精度。避免关键帧过早的固定,保证被充分优化。
- 其他的关键帧要均匀分布在空间中,丢弃有最大距离的,使得视差最大:
s ( I i ) = d ( I 1 , I i ) ∑ j = 3 N t ( d ( I i , I j ) ) − 1 (1) s\left(I_{i}\right)=\sqrt{d\left(I_{1}, I_{i}\right)}\sum_{j=3}^{N_{t}}\left(d\left(I_{i}, I_{j}\right)\right)^{-1} \tag{1} s(Ii)=d(I1,Ii)j=3∑Nt(d(Ii,Ij))−1(1)
共视窗口是和时间窗口有共视关系的关键帧,要找到那些在最新关键帧空白区域有地图点投影的关键帧,具体的策略:
- 计算距离地图来确定耗尽区域,将时间窗口投影到最新关键帧,计算每个像素到最近地图点的距离。
- 选择具有最大数目投影点的旧关键帧,会剔除大于一定视角的点,来防止遮挡等情况。
- 更新距离地图
- 迭代执行第二步,直到选出足够数目,或者没有关键帧。
激活新地图点前,共视点已经完成投影,避免了提取重复的地图点,保证地图的一致性。
Robust Non-Linear PBA
LMCW的关键帧选取范围广,忽略了实际光度的不一致性,比如由于遮挡,光反射等
提出根据光度误差的分布来剔除外点:
ξ ∗ = argmin ξ − ∑ k n log p ( r k ∣ ξ ) (2) \xi^{*}=\underset{\xi}{\operatorname{argmin}}-\sum_{k}^{n} \log p\left(r_{k} | \boldsymbol{\xi}\right)\tag{2} ξ∗=ξargmin−k∑nlogp(rk∣ξ)(2)
均匀分布
若给定且均匀分布的误差 r k r_k rk,求导等于0,得到re-weight的最小二乘:
w ( r k ) = − ∂ log p ( r k ) ∂ r k 1 r k (3) w\left(r_{k}\right)=-\frac{\partial \log p\left(r_{k}\right)}{\partial r_{k}} \frac{1}{r_{k}} \tag{3} w(rk)=−∂rk∂logp(rk)rk1(3)
高斯分布
如果符合高斯分布,得到一个常数权重,所有点的同等对待,没法处理外点。
w n ( r k ) = 1 σ n 2 (4) w_{n}\left(r_{k}\right)=\frac{1}{\sigma_{n}^{2}} \tag{4} wn(rk)=σn21(4)
Student t分布
稠密和稀疏光度误差都比较适合,权重函数
w t ( r k ) = ν + 1 ν + ( r k σ t ) 2 , when μ = 0 (5) w_{t}\left(r_{k}\right)=\frac{\nu+1}{\nu+\left(\frac{r_{k}}{\sigma_{t}}\right)^{2}}, \quad \text { when } \mu=0 \tag{5} wt(rk)=ν+(σtrk)2ν+1, when μ=0(5)
t分布能快速处理误差,给一个低权重。
使用gradient free iterative Nelder-Mead method(NM单纯形替换法,速度慢)来最小化概率密度函数拟合分布,确定这个参数 ν \nu ν和 σ t \sigma _t σt,而不是固定一个值(如维度 ν = 5 \nu=5 ν=5)。在拟合t分布之前会剔除异常值,此时 σ ^ t \hat \sigma_t σ^t 的确定是Median Absolute Deviation (MAD),即 σ ^ = 1.4826 M A D \hat{\sigma}=1.4826 \mathrm{MAD} σ^=1.4826MAD,拒绝大于3倍方差的值。
M估计(Huber)
w h ( r k ) = { 1 σ n 2 if ∣ r k ∣ < λ λ σ n 2 ∣ r k ∣ otherwise (6) w_{h}\left(r_{k}\right)=\left\{\begin{array}{ll}{\frac{1}{\sigma_{n}^{2}}} & {\text { if }\left|r_{k}\right|<\lambda} \\ {\frac{\lambda}{\sigma_{n}^{2}\left|r_{k}\right|}} & {\text { otherwise }}\end{array}\right. \tag{6} wh(rk)={σn21σn2∣rk∣λ if ∣rk∣<λ otherwise (6)
λ = 1.345 σ n \lambda=1.345 \sigma_{n} λ=1.345σn for N ( 0 , σ n 2 ) \mathcal{N}\left(0, \sigma_{n}^{2}\right) N(0,σn2),这个值可以固定,也可以动态调节。
A. Implementation of the probabilistic model into the PBA
由于内点和外点的判定是动态的,会自动学习每个关键帧的误差分布,因此可以适用于不同的场景。在普通的关键帧上被认为是外点的,在一些挑战场景下会被认为是内点。
把这个误差分布作为权重加到目标函数,可能会每次迭代都改变目标函数,会使得优化降级。我们只在每个金字塔层的最开始计算误差分布,之后优化过程就固定。PBA结束最后会计算一次误差分布。
B. Outlier management
低于目标帧95%的误差分布结果,被认为是内点。对于挑战的关键帧上,阈值会更高,相对宽松。对于普通帧,阈值降低,会更加严格。外点率大于30%就直接扔掉这个观测,如果优化中外点率大于60%就直接放弃这个优化。
要保留一个新点,必须在创建新关键帧后在所有新关键帧中对其进行观察,而在三个关键帧中对其进行观察则将其视为成熟点。 如果观察次数少于三个,则将删除成熟点。
Front-End
新的帧跟踪局部地图,地图点和参考关键帧被固定。使用coarse-to-fine优化,同时使用逆向组合法来避免jacobian的重新计算。
关键帧的判断(相对于最新关键帧):
- 地图点的可视率(visibility ratio)
s u = ∑ min ( p z p z ′ , 1 ) N s_u = \frac{\sum \min(\frac{p_z}{p_z^\prime},1)}{N} su=N∑min(pz′pz,1)
其中 N N N是最新关键帧可见点总数, p z , p z ′ p_z, p_z^\prime pz,pz′分别是最新关键帧和跟踪帧的点逆深度。这个的作用是当相机靠近一个物体时,会创建更多的关键帧。
- 跟踪帧的基线长度
s t = ∥ t ρ ‾ ∥ 2 s_t = \|\mathbf t\overline{\rho}\|^2 st=∥tρ∥2
定义为帧间位移和跟踪局部地图上平均逆深度的比。作用相当于平移的距离足够大,超出视线范围
- 光照变化
s a = ∣ a k − a i ∣ s_a = |a_k - a_i| sa=∣ak−ai∣
如果加权后的满足,则设置为关键帧。
ω u s u + ω t s t + ω a s a > 1 \omega_us_u+\omega_ts_t+\omega_as_a > 1 ωusu+ωtst+ωasa>1
跟踪新地图点
点会更新几帧后有低不确定性才被加入PBA,这种推迟的策略需要较好的初始值。为了保证有足够的点来激活,候选点在移出LMCW时才会被清除。激活的点是投影在空白区域的,当回到来过的地方,激活的点很少。
Discussion
需要一个重识别的功能,因为对于大场景,当误差累积较大时,可能有些点是没法重新投影过来的。