java-利用前序和中序遍历重建二叉树

如果只给出一个二叉树的前序遍历和中序遍历怎么重建起一个二叉树呢？

在剑指offer上给出这个题目，前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}。

思路：先来分析一下前序遍历和中序遍历得到的结果，

前序遍历第一位是根节点；
中序遍历中，根节点左边的是根节点的左子树，右边是根节点的右子树。

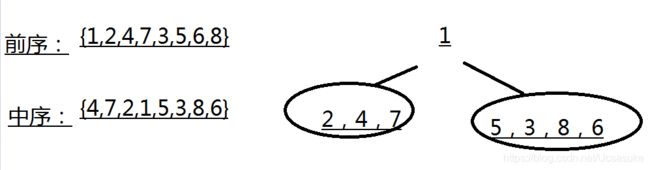
首先，根节点 是{ 1 }；
左子树是：前序{ 2,4,7 } ，中序{ 4,7,2 }；
右子树是：前序{ 3,5,6,8 } ，中序{ 5,3,8,6 }；

这时，如果我们把左子树和右子树分别作为新的二叉树，则可以求出其根节点，左子树和右子树。

以此类推，重复这个步骤就可以重建二叉树了。

1.首先根据前序遍历我们可以知道根节点为1，然后在中序遍历中找到1，我们可以知道1的左边是左子树即4，7，2 。右子树是1的右边即5，3，8，6。

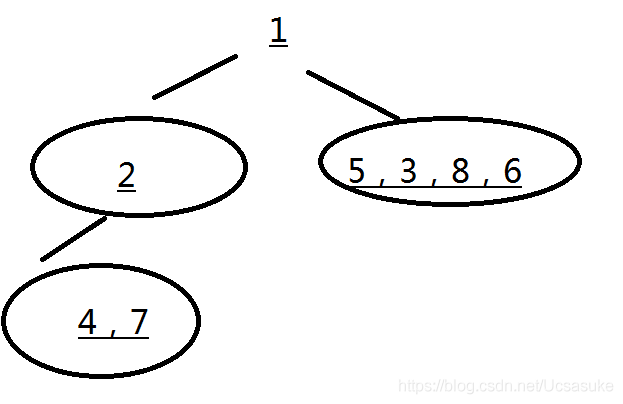
2.2，4，7 也是一棵二叉树，他也是二叉树，我们可不能区别对待，所以理应也满足先序遍历，先根再左最后右。那么2就是这颗小二叉树的根节点啦。

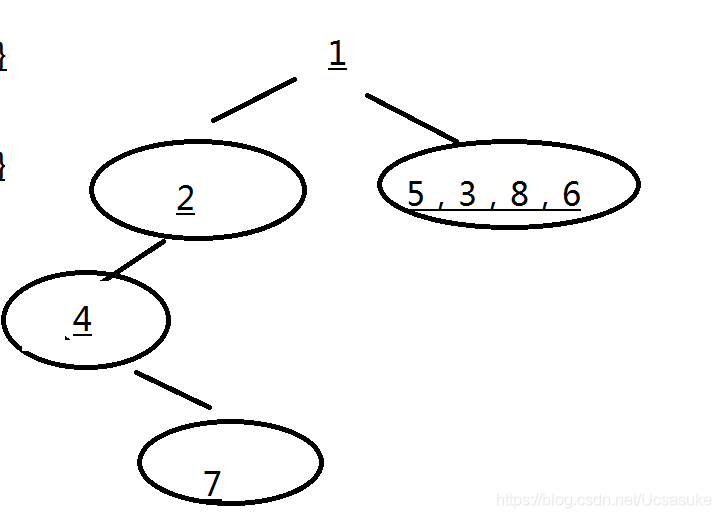
3.找到了小二叉树的根节点，按照先序再走左，发现4，7也是一棵二叉树，这颗小小二叉树也得满足先序哦，4为根节点，再走左，发现左没了，还记得先序得遍历规则嘛 先根再左后右，左没了那就轮到右啦，所以应该走7了，走完7以后，4，7这棵小小小二叉树算是走完了，走完之后该走2，4，7这颗小二叉树的右节点了。

而右子树相同方法去得出。

测试代码利用递归实现:

根据参数传入的前序pre和中序in数组
public void rebuild(T[] pre, T[] in) {
    this.root = rebuild(pre,0,pre.length-1,in,0,in.length-1);
}

//pre前序数组的[i,j]数据范围，in中序数组的[m,n]数据范围
private BSTNode rebuild(T[] pre, int i, int j, T[] in, int m, int n) {
    if (i > j || m > n) {
        return null;
    }

    BSTNode node = new BSTNode<>(pre[i], null, null);
    for (int k = m; k <= n; ++k) {
        // 在中序数组种找到根节点pre[i]         m, k-1   k+1,n
        if (pre[i].compareTo(in[k]) == 0) {
            node.setLeft(rebuild(pre, i + 1, i + (k - m), in, m, k - 1));
            node.setRight(rebuild(pre, i + (k - m) + 1, j, in, k + 1, n));
            break;
        }
    }
    return node;
}