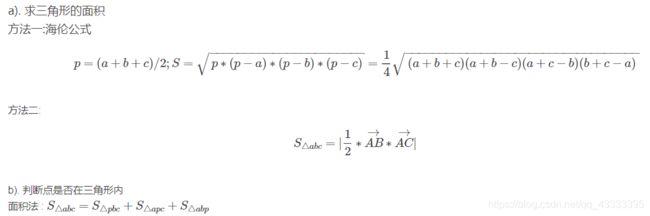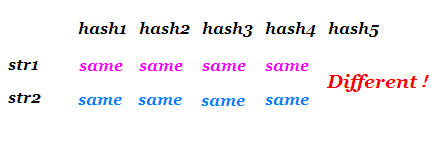ACM巨全模板(下)
柯氏模板(下)
柯氏模板(上)
柯氏模板(中)
pdf下载
本模板博主还在完善ing…谢谢大家观看
计算几何:
1.三角形 (求面积))
2.多边形
3.三点求圆心和半径
4.扫描线 (矩形覆盖求面积) (矩形覆盖求周长)
5.凸包 (平面上最远点对)
6.求凸多边形的直径
7.求凸多边形的宽度
8.求凸多边形的最小面积外接矩形
9.半平面交
字符串:
1.字典树(多个字符串的前缀)
2.KMP(关键字搜索)
3.EXKMP(找到S中所有P的匹配)
4.马拉车(最长回文串)
5.寻找两个字符串的最长前后缀(KMP)
6.hash(进制hash,无错hash,多重hash,双hash)
7.后缀数组 (按字典序排字符串后缀)
8.前缀循环节(KMP的fail函数)
9.AC自动机 (n个kmp)
10.后缀自动机
小技巧:
1.关于int,double强转为string
2.输入输出挂
3.低精度加减乘除
4.一些组合数学公式
5.二维坐标的离散化
6.消除向下取整的方法
7.一些常用的数据结构 (STL)
8.Devc++的使用技巧
9.封装好的一维离散化
10.Ubuntu对拍程序
11.常数
12.Codeblocks使用技巧
13.java大数
叮嘱
计算几何
1.点
a) 判断点是否在先线段上
1)首先判断Q是否在直线 P 1 P 2 P_1P_2 P1P2上。
判断方法:用叉乘,Q P 1 P_1 P1 × P 1 P 2 P_1P_2 P1P2 = 0,即(Q - P 1 P_1 P1) *( P 1 − P 2 P_1 - P_2 P1−P2) = 0;
2)考虑Q是否在 P 1 P 2 P_1P_2 P1P2的反向延迟线上,即Q在以 P 1 、 P 2 P_1、P_2 P1、P2为对角顶点的矩形内。
#includeb) 点绕点旋转后的坐标:
在平面中,一个点绕任意点旋转θ度后的点的坐标:
假设对图片上任意点(x,y),绕一个坐标点(rx0,ry0)逆时针旋转a角度后的新的坐标设为(x0, y0),有公式:
x0= (x - rx0)*cos(a) - (y - ry0)*sin(a) + rx0 ;
y0= (x - rx0)*sin(a) + (y - ry0)*cos(a) + ry0 ;
2.三角形
2.多边形
a) . 凸多边形面积的求法:
把凸多边形分成n-2个小三角形然后求面积 ( 对非凸多边形仍然有效 )
代码实现:
3.三点求圆心及半径
#include4.扫描线
a)矩形覆盖求面积
#define mem(a,x) memset(a,x,sizeof(a))
#includeb)矩形覆盖求周长
#define mem(a,x) memset(a,x,sizeof(a))
#include扫描线模板:
#include5.凸包
a)平面最远点对
#include 6.求凸多边形的直径:
多边形的直径是凸多边形边上所有点中距离最远的一对点的距离,他显然是某对对踵点的距离,枚举所有对踵点即可效率O(n)(对每一对对踵点O(1))
double RotatingCaliper_diameter(Point poly[],int n){
int p=0,q=n-1,fl,i;
double ret=0;
for(i=0;i<n;i++){
if(poly[i].y>poly[q].y) q=i;
if(poly[i].y<poly[p].y) p=i;
}
Point ymin=poly[p],ymax=poly[q];
for(i=0;i<n*3;i++){
if(ret<Length(poly[p%n]-poly[q%n])) ret=Length(poly[p%n]-poly[q%n]);
fl=dcmp(Cross(poly[(p+1)%n]-poly[p%n],poly[q%n]-poly[(q+1)%n]));
if(!fl){
if(ret<Length(poly[p%n]-poly[(q+1)%n])) ret=Length(poly[p%n]-poly[(q+1)%n]);
if(ret<Length(poly[q%n]-poly[(p+1)%n])) ret=Length(poly[q%n]-poly[(p+1)%n]);
p++,q++;
}
else{
if(fl>0) p++;
else q++;
}
}
return ret;
}//用旋转卡壳求解凸多边形直径
7.求凸多边形的宽度:
double RotatingCaliper_width(Point poly[],int n){
int p=0,q=n-1,fl,i;
double ret;
for(i=0;i<n;i++){
if(poly[i].y>poly[q].y) q=i;
if(poly[i].y<poly[p].y) p=i;
}
ret=Length(poly[p]-poly[q]);
for(i=0;i<n*3;i++){
fl=dcmp(Cross(poly[(p+1)%n]-poly[p%n],poly[q%n]-poly[(q+1)%n]));
if(!fl){
if(ret>DistanceToLine(poly[p%n],poly[q%n],poly[(q+1)%n])) ret=DistanceToLine(poly[p%n],poly[q%n],poly[(q+1)%n]);
p++,q++;
}
else{
if(fl>0){
if(ret>DistanceToLine(poly[q%n],poly[p%n],poly[(p+1)%n])) ret=DistanceToLine(poly[q%n],poly[p%n],poly[(p+1)%n]);
p++;
}
else{
if(ret>DistanceToLine(poly[p%n],poly[q%n],poly[(q+1)%n])) ret=DistanceToLine(poly[p%n],poly[q%n],poly[(q+1)%n]);
q++;
}
}
}
return ret;
}//用旋转卡壳求解凸多边形宽度
Rotating Caliper Width
8.求凸多边形的最小面积外接矩形:
这样的矩形一定与凸多边形至少一边发生重合,于是这一条重合的边以及这条边的对边可以通过旋转卡壳来枚举,在枚举出这么一组有重合平行边之后,如何枚举另外一对平行边呢,在我们枚举出第一对有重合平行边并找到其对应的另一对边之后(这个另一对边方向与有重合平行边垂直,所以这对边其实可以存成多边形上的一对点)如果我们旋转这组有重合平行边得到另一组有重合平行边的话,新的一组的对应另一对边可以由旧的一组通过向相同的方向旋转得来,判定是否完成旋转的方法可以是向量叉积效率O(n)(对每一对对踵点O(1),另一对平行线的旋转也是单向的于是也是O(n))其实求最小周长外接矩形也是同理
void RC(Poi poly[],int n){
int p=0,q=n-1,l=0,r=n-1;
int fl,i,j;
Vec nm,dr;
for(i=0;i<n;i++){
if(poly[i].y<poly[p].y) p=i;
if(poly[i].y>poly[q].y) q=i;
if(poly[i].x<poly[l].x) l=i;
if(poly[i].x>poly[r].x) r=i;
}
an[0]=intersect_p(poly[p],Vec(1,0),poly[l],Vec(0,1)),an[1]=intersect_p(poly[p],Vec(1,0),poly[r],Vec(0,1));
an[2]=intersect_p(poly[r],Vec(0,1),poly[q],Vec(1,0)),an[3]=intersect_p(poly[l],Vec(0,1),poly[q],Vec(1,0));
ans=fabs(Area(an[0],an[1],an[2]));
for(i=0;i<n*3;i++){
fl=dcmp(Cross(poly[(p+1)%n]-poly[p%n],poly[q%n]-poly[(q+1)%n]));
if(!fl){
dr=poly[(p+1)%n]-poly[p%n],dr=dr/Len(dr);
nm=Vec(dr.y,-dr.x);
while(dcmp(Cross(poly[(l+1)%n]-poly[l%n],nm))>0) l++;
nm=Vec(0,0)-nm;
while(dcmp(Cross(poly[(r+1)%n]-poly[r%n],nm))>0) r++;
cha[0]=intersect_p(poly[p%n],dr,poly[l%n],nm),cha[1]=intersect_p(poly[p%n],dr,poly[r%n],nm);
cha[2]=intersect_p(poly[r%n],nm,poly[q%n],dr),cha[3]=intersect_p(poly[l%n],nm,poly[q%n],dr);
if(fabs(Area(cha[0],cha[1],cha[2]))<ans){
for(j=0;j<4;j++) an[j]=cha[j];
ans=fabs(Area(an[0],an[1],an[2]));
}
}
else{
if(fl>0){
dr=poly[(p+1)%n]-poly[p%n],dr=dr/Len(dr);
nm=Vec(dr.y,-dr.x);
while(dcmp(Cross(poly[(l+1)%n]-poly[l%n],nm))>0) l++;
nm=Vec(0,0)-nm;
while(dcmp(Cross(poly[(r+1)%n]-poly[r%n],nm))>0) r++;
cha[0]=intersect_p(poly[p%n],dr,poly[l%n],nm),cha[1]=intersect_p(poly[p%n],dr,poly[r%n],nm);
cha[2]=intersect_p(poly[r%n],nm,poly[q%n],dr),cha[3]=intersect_p(poly[l%n],nm,poly[q%n],dr);
if(fabs(Area(cha[0],cha[1],cha[2]))<ans){
for(j=0;j<4;j++) an[j]=cha[j];
ans=fabs(Area(an[0],an[1],an[2]));
}
p++;
}
else{
dr=poly[(q+1)%n]-poly[q%n],dr=dr/Len(dr);
nm=Vec(-dr.y,dr.x);
while(dcmp(Cross(poly[(l+1)%n]-poly[l%n],nm))>0) l++;
nm=Vec(0,0)-nm;
while(dcmp(Cross(poly[(r+1)%n]-poly[r%n],nm))>0) r++;
cha[0]=intersect_p(poly[p%n],dr,poly[l%n],nm),cha[1]=intersect_p(poly[p%n],dr,poly[r%n],nm);
cha[2]=intersect_p(poly[r%n],nm,poly[q%n],dr),cha[3]=intersect_p(poly[l%n],nm,poly[q%n],dr);
if(fabs(Area(cha[0],cha[1],cha[2]))<ans){
for(j=0;j<4;j++) an[j]=cha[j];
ans=fabs(Area(an[0],an[1],an[2]));
}
q++;
}
}
}
}
9.半平面交
半平面交是什么?
我们知道一条直线可以把平面分为两部分,其中一半的平面就叫半平面。
那半平面交,就是多个半平面的相交部分。我们在学习线性规划时就有用过。
半平面交有什么用?
1.求解一个区域,可以看到给定图形的各个角落。(多边形的核)
2.求可以放进多边形的圆的最大半径。
给你n个凸多边形,求多边形的交的面积
#include 字符串:
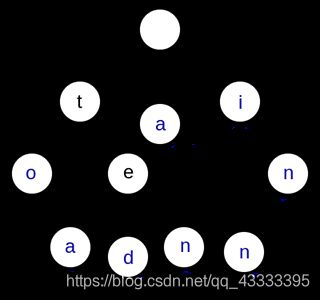
1.字典树(多个字符串的前缀)
1.求该字符串是否是众多字符串中的子字符串。(小写字母abc)
/*
trie tree的储存方式:将字母储存在边上,边的节点连接与它相连的字母
trie[rt][x]=tot:rt是上个节点编号,x是字母,tot是下个节点编号
*/
#include2、查询前缀出现次数(小写字母abc)
/*
trie tree的储存方式:将字母储存在边上,边的节点连接与它相连的字母
trie[rt][x]=tot:rt是上个节点编号,x是字母,tot是下个节点编号
*/
#include2.KMP(关键字搜索)
next数组:
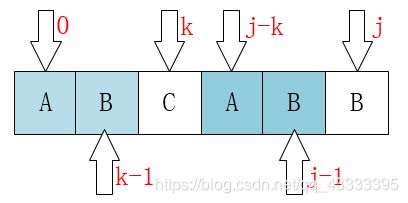
复杂度O(m+n)
计算匹配串在模式串中第一次出现的位置:
#include 3.EXKMP(找到S中所有P的匹配)
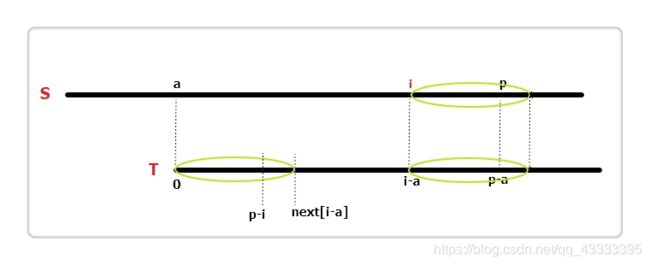
next[i]:T[i]…T[m - 1]与T的最长相同前缀长度;
extend[i]:S[i]…S[n - 1]与T的最长相同前缀长度。
本代码输出的是next和extend数组,当next数组与p字符串长度相同即是s中p的匹配,复杂度O(n+m)
#include 4.马拉车(最长回文串)
复杂度O(n)
找出类似"abba"和“abcba”
#include 5.寻找两个字符串的最长前后缀(KMP)
复杂度O(n+m).
#include6.hash
1.进制hash(单哈希/自然溢出法)
给出一个固定进制base,将一个串的每一个元素看做一个进制位上的数字,所以这个串就可以看做一个base进制的数,那么这个数就是这个串的哈希值;则我们通过比对每个串的的哈希值,即可判断两个串是否相同
#include2.无错hash
其实原理很简单,就是我们要记录每一个已经诞生的哈希值,然后对于每一个新的哈希值,我们都可以来判断是否和已有的哈希值冲突,如果冲突,那么可以将这个新的哈希值不断加上一个大质数,直到不再冲突。
for(int i=1;i<=m;i++)//m个串
{
cin>>str;//下一行的check为bool型
while(check[hash(str)])hash[i]+=19260817;
hash[i]+= hash(str) ;
}
3.多重hash
这其实就是你用不同的两种或多种方式哈希,然后分别比对每一种哈希值是否相同——显然是增加了空间和时间,但也确实增加了其正确性。
//哈希自动机,需要二维hash数组
for伪代码排序,用来使哈希值单调(更好判断相/不同的数量)
for(int i=1;i<=m;i++){
check=1;
for(int j=1;j<=qwq;j++)//皮一下
if(hash[j][i]==hash[j][i+1]){check=0;break;}
if(check)ans++;//此为判断相同个数
}
4.双hash
其实就是用两个不同的mod来算hash,哈希冲突的概率是降低了很多,不过常数大,容易被卡
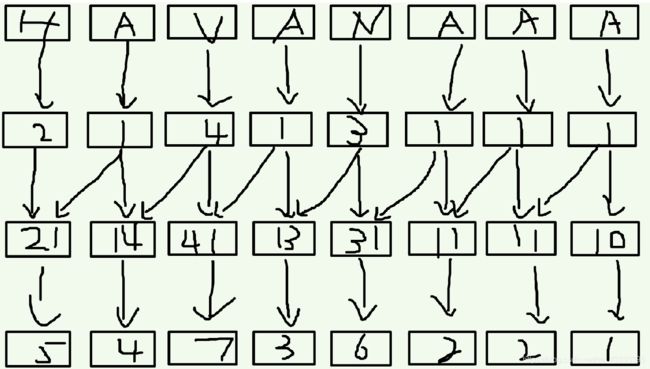
#include7.后缀数组
后缀就是从字符串的某个位置i到字符串末尾的子串,我们定义以s的第i个字符为第一个元素的后缀为suff(i)
把s的每个后缀按照字典序排序,
后缀数组sa[i] 就表示排名为i的后缀的起始位置的下标
而它的映射数组rk[i]就表示起始位置的下标为i的后缀的排名
简单来说,sa表示排名为i的是啥,rk表示第i个的排名是啥
两个优化:
- 1.倍增
1)先按照每个后缀的第一个字符排序。
2)再把相邻的两个关键字合并到一起,就相当于根据每一个后缀的前两个字符进行排序。第二关键字的补零。(2倍数排序) 直到没有相同为止。
- 2.基数排序
用一波基数排序优化一下。在这里我们可以注意到,每一次排序都是排两位数,所以基数排序可以将它优化到O(n)级别,总复杂度就是(n log n)。
构造最长公共前缀——Height
同样先是定义一些变量
Heigth[i] : 表示Suffix[SA[i]]和Suffix[SA[i - 1]]的最长公共前缀,也就是排名相邻的两个后缀的最长公共前缀
H[i] : 等于Height[Rank[i]],也就是后缀Suffix[i]和它前一名的后缀的最长公共前缀
而两个排名不相邻的最长公共前缀定义为排名在它们之间的Height的最小值。
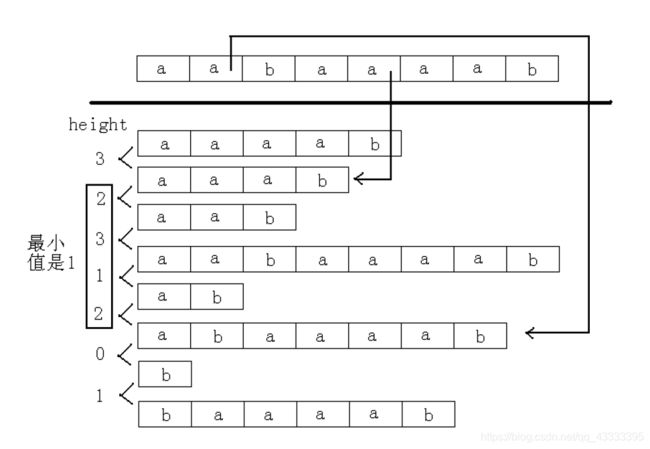
高效地得到Height数组
想要快速的得到Height就需要用到一个关于H数组的性质。
H[i] ≥ H[i - 1] - 1!
如果上面这个性质是对的,那我们可以按照H[1]、H[2]……H[Len] 的顺序进行计算,那么复杂度就降为O(N)了!
让我们尝试一下证明这个性质 : 设Suffix[k]是排在Suffix[i - 1]前一名的后缀,则它们的最长公共前缀是H[i - 1]。都去掉第一个字符,就变成Suffix[k + 1]和Suffix[i]。如果H[i - 1] = 0或1,那么H[i] ≥ 0显然成立。 否则,H[i] ≥ H[i - 1] - 1(去掉了原来的第一个,其他前缀一样相等), 所以Suffix[i]和在它前一名的后缀的最长公共前缀至少是H[i - 1] - 1。
仔细想想还是比较好理解的。H求出来,那Height就相应的求出来了,这样结合SA,Rank和Height我们就可以做很多关于字符串的题了!
例题:
读入一个长度为n的由大小写英文字母或数字组成的字符串,请把这个字符串的所有非空后缀按字典序从小到大排序,然后按顺序输出后缀的第一个字符在原串中的位置。位置编号为1到n。
按字典序排字符串后缀
#include一个串中两个串的最大公共前缀是多少?
这不就是Height吗?用rmq预处理,再O(1)查询。
8.前缀循环节(KMP的fail函数)
对于具有n个字符的给定字符串的每个前缀s (每个字符具有介于97和126,包含在内),我们想知道前缀是否是周期字符串。也就是说,对于每个i ( 2 ≤ i ≤ n ) (2≤i≤n) (2≤i≤n)我们想知道最大的k>1 (如果有) 这样的前缀s的长度i可以是写为a k,这是连接k次,对于某些字符串a的缀。当然,我们还想知道周期k。
str :aabaabaabaab
fail:-1 0 1 0 1 2 3 4 5 6 7 8 9
output:
2 2
6 2
9 3
12 4
fail[i]>=0&&i%(i-fail[i])==0 判断前缀是否循环
k=i/(i-fail[i]) 循环的次数
#include 9.AC自动机
#include 10.后缀自动机
#include小技巧:
1.关于int,double强转为string
直接看代码,又暴力,又愉快。
int a=520;
float b=5.20;
string str="dong";
string res=str+to_string(a);
cout<<res<<endl; //dong520
res=str+to_string(b);
res.resize(8); //控制字符串的大小
cout<<res<<endl; //dong5.20
2.输入输出挂
直接a=read()读入,out(a)输出;
template <typename T>
void read(T &x)
{
x = 0;
int f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = (x << 1) + (x << 3) + (ch ^ 48);
ch = getchar();
}
x *= f;
return;
}
template <typename T>
void write(T x)
{
if (!x)
{
putchar('0');
return;
}
char F[40];
T tmp = x > 0 ? x : -x;
if (x < 0)
putchar('-');
int cnt = 0;
while (tmp > 0)
{
F[cnt++] = tmp % 10 + '0';
tmp /= 10;
}
while (cnt > 0)
putchar(F[--cnt]);
}
4.一些组合数学公式
5.二维坐标的离散化
坐标(3,2000),(10005,31),(10006,5)
离散为(1,5),(3,3),(4,1)。
#include
maxx=max(maxx,newx); //找最大上边界
maxy=max(maxy,newy); //找最大左边界
m[newx][newy]=1;
}
}
int main(){
int A,B,N;
scanf("%d %d %d",&A,&B,&N); //输入长度宽度和点的个数
for(int i=0;i<N;i++) {
scanf("%d %d",&node[i].x,&node[i].y); //输入点的坐标
x[i+1]=node[i].x;
y[i+1]=node[i].y;
}
discrete(N);
for(int i=0;i<=maxx;i++){ //输出离散化后的图
for(int j=0;j<=maxy;j++){
printf("%d ",m[i][j]);
}printf("\n");
}
}
6.消除向下取整的方法
a)
7.一些常用的数据结构 (STL)
a)bitset
C++的 bitset 在 bitset 头文件中,它是一种类似数组的结构,它的每一个元素只能是0或1,每个元素仅用1bit空间。
bitset<4> bitset1; //无参构造,长度为4,默认每一位为0
bitset<8> bitset2(12); //长度为8,二进制保存,前面用0补充
string s = "100101";
bitset<10> bitset3(s); //长度为10,前面用0补充
char s2[] = "10101";
bitset<13> bitset4(s2); //长度为13,前面用0补充
cout << bitset1 << endl; //0000
cout << bitset2 << endl; //00001100
cout << bitset3 << endl; //0000100101
cout << bitset4 << endl; //0000000010101
用字符串构造时,字符串只能包含 ‘0’ 或 ‘1’ ,否则会抛出异常。
构造时,需在<>中表明bitset 的大小(即size)。
在进行有参构造时,若参数的二进制表示比bitset的size小,则在前面用0补充(如上面的栗子);若比bitsize大,参数为整数时取后面部分,参数为字符串时取前面部分.
bitset对于二进制有位操作符
此外,可以通过 [ ] 访问元素(类似数组),注意最低位下标为0
bitset<8> foo ("10011011");
cout << foo.count() << endl; //5 (count函数用来求bitset中1的位数,foo中共有5个1
cout << foo.size() << endl; //8 (size函数用来求bitset的大小,一共有8位
cout << foo.test(0) << endl; //true (test函数用来查下标处的元素是0还是1,并返回false或true,此处foo[0]为1,返回true
cout << foo.test(2) << endl; //false (同理,foo[2]为0,返回false
cout << foo.any() << endl; //true (any函数检查bitset中是否有1
cout << foo.none() << endl; //false (none函数检查bitset中是否没有1
cout << foo.all() << endl; //false (all函数检查bitset中是全部为1
bitset<8> foo ("10011011");
cout << foo.flip(2) << endl; //10011111 (flip函数传参数时,用于将参数位取反,本行代码将foo下标2处"反转",即0变1,1变0
cout << foo.flip() << endl; //01100000 (flip函数不指定参数时,将bitset每一位全部取反
cout << foo.set() << endl; //11111111 (set函数不指定参数时,将bitset的每一位全部置为1
cout << foo.set(3,0) << endl; //11110111 (set函数指定两位参数时,将第一参数位的元素置为第二参数的值,本行对foo的操作相当于foo[3]=0
cout << foo.set(3) << endl; //11111111 (set函数只有一个参数时,将参数下标处置为1
cout << foo.reset(4) << endl; //11101111 (reset函数传一个参数时将参数下标处置为0
cout << foo.reset() << endl; //00000000 (reset函数不传参数时将bitset的每一位全部置为0
bitset<8> foo ("10011011");
string s = foo.to_string(); //将bitset转换成string类型
unsigned long a = foo.to_ulong(); //将bitset转换成unsigned long类型
unsigned long long b = foo.to_ullong(); //将bitset转换成unsigned long long类型
cout << s << endl; //10011011
cout << a << endl; //155
cout << b << endl; //155
数学公式的推导:
Σ(|l-x|+|r-x|)最小,那么x就是所有l,r的中位数了
8.Devc++的使用技巧
1,改变字体:
工具–编辑器选项–显示
推荐:Consolas
2.改变背景和高亮
工具–编辑器选项–语法
推荐:Twilight
3.自动保存
工具–编辑器选项–自动保存
4.代码补全
工具–编辑器选项–代码补全(打开)
5.中文
tool–Environment Operation–Language
工具栏右键可关闭工具栏,也可设置快捷键
调试打开:
工具–编译器选项–代码生成/优化–连接器–产生调试信息(YES)(打开项目管理)
调试:
先编译(F9)–在调试(F5)–设置断点–在黑框输入样例–添加查看(可查看变量)–下一步
快捷键:
ctrl+shift+A 补全
ctrl+R 一键替换
F9 编译
F10 运行
F11 编译运行
ctrl+F11 全屏
ctrl+N 创建文件
ctrl+W 删除文件
ctrl+C 强制结束
ctrl+Z 终止运行
ctrl+S 保存
ctrl+M 分屏
ctrl+E 复制行
ctrl+D 删除行
9.封装好的一维离散化
int discretization(int *origin_data, int *discrete_data, int size_data) { //started index is 1
for (int i = 1; i <= size_data; ++i)
discrete_data[i] = origin_data[i];
sort(discrete_data + 1, discrete_data + 1 + size_data);
int size_discreted = unique(discrete_data + 1, discrete_data + 1 + size_data) - (discrete_data + 1);
for (int i = 1; i <= size_data; ++i)
origin_data[i] = lower_bound(discrete_data + 1, discrete_data + 1 + size_discreted, origin_data[i]) - discrete_data;
return size_discreted;
}
10.Ubuntu对拍程序
cpp
freopen("in","r",stdin);
freopen("1.out","w",stdout);
freopen("in","r",stdin);
freopen("2.out","w",stdout);
对拍程序
#include数据生成器
#include11.常数
const ull hash1 = 1610612741;
//const ull hash2 = 1610612747;
const double _PI = 3.14159265358979323846; // PI
const double _1_PI = 0.31830988618379067154; // 1/PI
const double _2_SQRTPI = 1.12837916709551257390; // 2/sqrt(PI)
12.codeblocks 的使用技巧
字体:
setting→editor→general settings→choose→Consolas
颜色:
setting→editor→syntax highlighting
色调85 饱和度123 亮度205.(豆沙绿)
风格:
更改风格为java括号在行末
1.Setting->Editor->Source Formatter->style->Bracket style 修改成Java
2.Setting->Editor->Source Formatter->padding ->Insert space padding around operators 打勾
快捷键:
Ctrl+R可以替换;
Ctrl+Shift+C 注释掉当前行或者选中快 Ctrl+Shift+x 解除注释
编译运行F9
补全:
进Settings里的Editor:
在general settings →Code-completion中,
将Automatically launch when typed # letter中的4改成2,这样打两个字母就会有提示了。
在Code-completion中:
• 将Keyword sets to additionally include中1到9都勾上
将Delay for auto-kick-in when typing [.::->]拉到 200ms,这样快点出来提示
• 选中Case-sensitive match,防止一些无关的东西干扰,如果你想它帮你纠正大小写,那就去掉勾
设置快捷键:
进Settings里的Editor:
在Keyboard short-cuts中将Edit->Code complete的快捷键
save改为ctrl+s
改为shift+ f。
codeblocks如果无法调试:(必须创建项目)
有些下载的codeblocks没有自带MinGW,没法编译,当你自己下载一个MinGW,你安装好了,可能不会带有gdb.exe文件。
1.点击Settings,选择Debugger选项
2.点击Default,选择Executable path,选择一个gdb.exe的文件,这个文件就在安装MinGW的文件夹的bin里面
3.如果没有这个gdb.exe文件,你就在这个网站下面下载一个,http://www.equation.com/servlet/equation.cmd?fa=gdb
4.下载好的gdb.exe复制到你的安装MinGW的文件夹的bin里面,就可以进行调试了
5.有些编译环境是有中文这些的不能编译,要选择新建的项目才可以编译
13.java大数
构造器描述
BigDecimal(int) 创建一个具有参数所指定整数值的对象。
BigDecimal(double) 创建一个具有参数所指定双精度值的对象。
BigDecimal(long) 创建一个具有参数所指定长整数值的对象。
BigDecimal(String) 创建一个具有参数所指定以字符串表示的数值的对象。
方法描述
add(BigDecimal) BigDecimal对象中的值相加,然后返回这个对象。
subtract(BigDecimal) BigDecimal对象中的值相减,然后返回这个对象。
multiply(BigDecimal) BigDecimal对象中的值相乘,然后返回这个对象。
divide(BigDecimal) BigDecimal对象中的值相除,然后返回这个对象。
toString() 将BigDecimal对象的数值转换成字符串。
doubleValue() 将BigDecimal对象中的值以双精度数返回。
floatValue() 将BigDecimal对象中的值以单精度数返回。
longValue() 将BigDecimal对象中的值以长整数返回。
intValue() 将BigDecimal对象中的值以整数返回。
//1753 求A+B
import java.math.*;
import java.util.*;
public class Main
{
public static void main(String args[]){
BigDecimal c = new BigDecimal("0");
BigDecimal d = new BigDecimal("0");
BigDecimal e = new BigDecimal("0");
BigDecimal f = new BigDecimal("0");
Scanner cin = new Scanner(System.in);
int n = cin.nextInt();
while(n!=0){//等价于!=EOF
n--;
BigDecimal a = cin.nextBigDecimal();
BigDecimal b = cin.nextBigDecimal();
c = a.add(b);
System.out.println(c.stripTrailingZeros().toPlainString());
d = a.divide(b); //可以是小数负数,但是不能是无限小数
System.out.println(d.stripTrailingZeros().toPlainString());
e = a.subtract(b);
System.out.println(e.stripTrailingZeros().toPlainString());
f = a.multiply(b);
System.out.println(f.stripTrailingZeros().toPlainString());
}
}
}
//1715 求斐波那契数列
import java.math.*;
import java.util.*;
public class Main
{
public static void main(String args[]){
BigDecimal a[] = new BigDecimal[1005];
Scanner cin = new Scanner(System.in);
while(cin.hasNext()){//等价于!=EOF
a[1] = a[2] = new BigDecimal("1");
for (int i =3; i< 1005; i++){
a[i] = a[i-1].add(a[i-2]);
}
int N = cin.nextInt();
for (int j = 0; j< N;j++){
int pi = cin.nextInt();
System.out.println(a[pi]);
}
}
}
//1042 求阶乘
import java.math.*;
import java.util.*;
public class Main
{
public static void main(String args[]){
Scanner cin = new Scanner(System.in);
while (cin.hasNext()){
// 计算阶乘
BigInteger c = new BigInteger("1");
int n = cin.nextInt();
for(int i = 1;i <= n; i++){
BigInteger s = BigInteger.valueOf(i);
c = c.multiply(s);
}
System.out.println(c);
}
}
}
//1063 求R的n次方,注意输出格式的要求
import java.math.*;
import java.util.*;
public class Main
{
public static void main(String args[]){
Scanner cin = new Scanner(System.in);
while (cin.hasNext()){
// 计算n方
BigDecimal r = cin.nextBigDecimal();
int n = cin.nextInt();
BigDecimal rn = new BigDecimal("1.0");
rn = r.pow(n).stripTrailingZeros();//去掉字符串最后面的0以及来消除BigDecimal用科学计数形式来表示结果
String tmp = rn.toPlainString();
//去掉前导0
if(tmp.startsWith("0"))
tmp=tmp.substring(1);
System.out.println(tmp);
}
}
}//1715 求斐波那契数列
import java.math.*;
import java.util.*;
public class Main
{
public static void main(String args[]){
BigDecimal a[] = new BigDecimal[1005];
Scanner cin = new Scanner(System.in);
while(cin.hasNext()){//等价于!=EOF
a[1] = a[2] = new BigDecimal("1");
for (int i =3; i< 1005; i++){
a[i] = a[i-1].add(a[i-2]);
}
int N = cin.nextInt();
for (int j = 0; j< N;j++){
int pi = cin.nextInt();
System.out.println(a[pi]);
}
}
}
叮嘱:
1.遇到第k大记得考虑二分
注意:
1.版权归本作者李炜柯所有;2.未经原作者允许不得转载本文内容,否则将视为侵权;3.转载或者引用本文内容请注明来源及原作者;
文章由多篇博客整理而成,如有侵权,请联系本作者qq:1315602340
希望此篇模板能帮助到大家