李宏毅机器学习作业2:Winner还是Losser（含训练数据）

训练数据以及源代码在我的Github：https://github.com/taw19960426/DeepLearning/tree/master/%E4%BD%9C%E4%B8%9A/%E4%BD%9C%E4%B8%9A2%E6%95%B0%E6%8D%AE

一、作业说明

给定训练集spam_train.csv，要求根据每个ID各种属性值来判断该ID对应角色是Winner还是Losser(收入是否大于50K)，这是一个典型的二分类问题。

• CSV文件，大小为4000行X59列;

• 4000行数据对应着4000个角色，ID编号从1到4001;

• 59列数据中， 第一列为角色ID，最后一列为分类结果，即label(0、1两种)，中间的57列为角色对应的57种属性值；

二、思路分析

2.1 思路分析

这是一个典型的二分类问题，结合课上所学内容，决定采用Logistic回归算法。

与线性回归用于预测不同，Logistic回归则常用于分类(通常是二分类问题)。Logistic回归实质上就是在普通的线性回归后面加上了一个sigmoid函数，把线性回归预测到的数值压缩成为一个概率，进而实现二分类（关于线性回归模型，可参考上一次作业）。

在损失函数方面，Logistic回归并没有使用传统的欧式距离来度量误差，而使用了交叉熵(用于衡量两个概率分布之间的相似程度)。
　　

2.2 数据预处理

在机器学习中，数据的预处理是非常重要的一环，能直接影响到模型效果的好坏。本次作业的数据相对简单纯净，在数据预处理方面并不需要花太多精力。

首先是空值处理(尽管没看到空值，但为了以防万一，还是做一下)，所有空值用0填充(也可以用平均值、中位数等，视具体情况而定)。

接着就是把数据范围尽量scale到同一个数量级上，观察数据后发现，多数数据值为0，非0值也都在1附近，只有倒数第二列和倒数第三列数据值较大，可以将这两列分别除上每列的平均值，把数值范围拉到1附近。

由于并没有给出这57个属性具体是什么属性，因此无法对数据进行进一步的挖掘应用。

上述操作完成后，将表格的第2列至58列取出为x(shape为4000X57)，将最后一列取出做label y(shape为4000X1)。进一步划分训练集和验证集，分别取x、y中前3500个样本为训练集x_test(shape为3500X57)，y_test(shape为3500X1)，后500个样本为验证集x_val(shape为500X57)，y_val(shape为500X1)。

数据预处理到此结束。

#数据的预处理
    df=pd.read_csv('spam_train.csv')#读文件
    df=df.fillna(0)#空值用0填充
    array=np.array(df)#转化为对象（4000，49）
    x=array[:,1:-1]#抛弃第一列和最后一列shape(4000,47)
    y=array[:,-1]#最后一列label
    #将倒数第二列和第三列除以平均值
    x[:,-1]=x[:,-1]/np.mean(x[:,-1])
    x[:, -2] = x[:, -2] / np.mean(x[:, -2])

    #划分测试集和验证集
    x_train=x[0:3500,:]
    y_train = y[0:3500]
    x_val=x[3500:4001,:]
    y_val=y[3500:4001]

2.3 模型建立

2.3.1 线性回归

先对数据做线性回归，得出每个样本对应的回归值。下式为对第n个样本$x^n$的回归，回归结果为$y^n$。

$${\mathrm{y}}^n=\sum _{i=1}^{57}{w}_i{x}_i^n+b$$

2.3.2 sigmoid函数压缩回归值

之后将回归结果送进sigmoid函数，得到概率值。
$$p^n=\frac{1}{1+e^{-y^n}}$$

2.3.3 误差反向传播

接着就到重头戏了。众所周知，不管线性回归还是Logistic回归，其关键和核心就在于通过误差的反向传播来更新参数，进而使模型不断优化。因此，损失函数的确定及对各参数的求导就成了重中之重。在分类问题中，模型一般针对各类别输出一个概率分布，因此常用交叉熵作为损失函数。交叉熵可用于衡量两个概率分布之间的相似、统一程度，两个概率分布越相似、越统一，则交叉熵越小；反之，两概率分布之间差异越大、越混乱，则交叉熵越大。

下式表示k分类问题的交叉熵，P为label，是一个概率分布，常用one_hot编码。例如针对3分类问题而言，若样本属于第一类，则P为(1,0,0)，若属于第二类，则P为(0,1,0)，若属于第三类，则为(0,0,1)。即所属的类概率值为1，其他类概率值为0。Q为模型得出的概率分布，可以是(0.1,0.8,0.1)等。
　　$${\mathrm{Loss}}^n=-\sum _1^k{P}^n\ln Q^n$$
针对本次作业而言，虽然模型只输出了一个概率值p，但由于处理的是二分类问题，因此可以很快求出另一概率值为1-p，即可视为模型输出的概率分布为Q(p，1-p)。将本次的label视为概率分布P(y,1-y)，即Winner(label为1)的概率分布为(1,0)，分类为Losser(label为0)的概率分布为(0,1)。
$${\mathrm{Loss}}^n=-\left[{\hat{y}}^n\ln p^n+\left(1-{\hat{y}}^n\right)\ln \left(1-p^n\right)\right]$$
损失函数对权重w求偏导，可得：
$$\frac{\partial Los{s}^n}{\partial w_i}=-x_i\left[{\hat{y}}^n-p^n\right]$$
同理，损失函数对偏置b求偏导，可得：
$$\frac{\partial Los{s}^n}{\partial b}=-\left[{\hat{y}}^n-p^n\right]$$
课件上的公式：

• 加正则化$${\mathrm{Loss}}^n=-\sum _1^k{p}^n\ln Q^n+\lambda {\left(w_i\right)}^2$$

• $${\mathrm{Loss}}^n=\sum _n-\left[{\hat{y}}^n\ln f_{w,b}\left(x^n\right)+\left(1-{\hat{y}}^n\right)\ln \left(1-f_{w,b}\left(x^n\right)\right)\right]$$

• $$\begin{array}{l}{f}_{w,b}(x)=\sigma (z)=1/1+\exp (-z)\end{array}$$

• $$z=w\cdot x+b=\sum _i{w}_i{x}_i+b$$

2.3.4 参数更新

求出梯度后，再拿原参数减去梯度与学习率的乘积，即可实现参数的更新。

#平均数
        b_g/=num
        w_g/=num

        #adagrad
        bg2_sum+=b_g**2
        wg2_sum+=w_g**2
        #更新w和b
        weights-=Learning_rate/wg2_sum**0.5*w_g
        bias-=Learning_rate/bg2_sum**0.5*b_g

三、代码分享与结果显示

3.1 源代码

import numpy as np
import pandas as pd

def train(x_train,y_train,epoch):
    num=x_train.shape[0]
    '''y.shape 返回的一个元组，代表 y 数据集的信息如（行，列）
    y.shape[0], 意思是：返回 y 中行的总数。这个值在 y 是单特征的情况下 和 len(y) 是等价的，
    即数据集中数据点的总数。'''
    dim=x_train.shape[1]
    bias=0#偏置初始化
    weights=np.ones(dim)#权重初始化
    Learning_rate=1#学习率和正则项系数初始化
    Regular_coefficient=0.001
    #用于存放偏置值的梯度平方和,adagrad用到
    bg2_sum=0
    wg2_sum=np.zeros(dim)

    #迭代求w,b
    for i in range(epoch):
        b_g=0#初始化
        w_g=np.zeros(dim)
       # 计算梯度，梯度计算时针对损失函数求导,在所有数据上
        for j in range(num):
            z=weights.dot(x_train[j,:])+bias#Z函数表达式
            sigmoid=1/(1+np.exp(-z))#sigmoid function
            #损失函数对b求导
            b_g+=((-1)*(y_train[j]-sigmoid))
            # 损失函数对w求导,并且有正则化（防overfitting)

            for k in range(dim):
                w_g[k]+=(-1)*(y_train[j]-sigmoid)*x_train[j,k]+2*Regular_coefficient*weights[k]
        #平均数
        b_g/=num
        w_g/=num

        #adagrad
        bg2_sum+=b_g**2
        wg2_sum+=w_g**2
        #更新w和b
        weights-=Learning_rate/wg2_sum**0.5*w_g
        bias-=Learning_rate/bg2_sum**0.5*b_g

    # 每训练3轮，输出一次在训练集上的正确率
    # 在计算loss时，由于涉及g()运到lo算，因此可能出现无穷大，计算并打印出来的loss为nan
    # 有兴趣的同学可以把下面涉及到loss运算的注释去掉，观察一波打印出的loss
        if i%3==0:
            Correct_quantity=0
            result=np.zeros(num)
            #loss=0
            for j in range(num):
                z = weights.dot(x_train[j, :]) + bias  # Z函数表达式
                sigmoid = 1 / (1 + np.exp(-z))  # sigmoid function
                if sigmoid>=0.5:
                    result[j]=1
                else:
                    result[j]=0
                if result[j]==y_train[j]:
                    Correct_quantity+=1.0
                #loss += (-1) * (y_train[j] * np.ln(sigmoid) + (1 - y_train[j]) * np.ln(1 - sigmoid))
            #print(f"epoch{0},the loss on train data is::{1}", i, loss / num)
            print(f"epoch{0},the Correct rate on train data is:{1}",i,Correct_quantity/num)
    return weights,bias

#对求出来的W和b验证一下效果
def validate(x_val,y_val,weights,bias):
    num=x_val.shape[0]
    Correct_quantity = 0
    result = np.zeros(num)
    loss=0
    for j in range(num):
        z = weights.dot(x_val[j, :]) + bias  # Z函数表达式
        sigmoid = 1 / (1 + np.exp(-z))  # sigmoid function
        if sigmoid >= 0.5:
            result[j] = 1
        if sigmoid < 0.5:
            result[j] = 0
        if result[j] == y_val[j]:
            Correct_quantity += 1.0
        #验证集上的损失函数
        #loss += (-1) * (y_val[j] * np.log(sigmoid) + (1 - y_val[j]) * np.ln(1 - sigmoid))

    return Correct_quantity/num


def main():
    #数据的预处理
    df=pd.read_csv('spam_train.csv')#读文件
    df=df.fillna(0)#空值用0填充
    array=np.array(df)#转化为对象（4000，49）
    x=array[:,1:-1]#抛弃第一列和最后一列shape(4000,47)
    y=array[:,-1]#最后一列label
    #将倒数第二列和第三列除以平均值
    x[:,-1]=x[:,-1]/np.mean(x[:,-1])
    x[:, -2] = x[:, -2] / np.mean(x[:, -2])

    #划分测试集和验证集
    x_train=x[0:3500,:]
    y_train = y[0:3500]
    x_val=x[3500:4001,:]
    y_val=y[3500:4001]

    #迭代次数为30次
    epoch=30
    w,b=train(x_train,y_train,epoch)
    #验证集上的结果
    Correct_rate=validate(x_val,y_val,w,b)
    print(f"The Correct rate on val data is:{0}",Correct_rate)

if __name__ == '__main__':
    main()

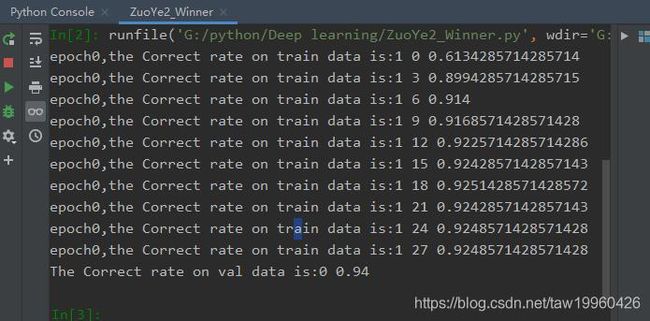
3.2 结果显示

可以看出，在训练30轮后，分类正确率能达到94%左右。

参考资料：

• https://www.cnblogs.com/HL-space/p/10785225.html
• http://www.luyixian.cn/news_show_4755.aspx
• https://www.cnblogs.com/luhuan/p/7925790.html
• https://blog.csdn.net/u013541048/article/details/81335256