并查集入门篇（Exile）

1 概念

并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间内计算出试题需要的结果，只能用并查集来描述。

并查集是一种可以动态维护若干不重叠的集合，并支持合并与查询的数据结构。
常常在使用中以森林来表示。

2 主要操作

在说主要操作之前，我们要知道集合是如何存储的。
我们用一个树形结构存储每个集合，树上的每个节点是一个元素，树根是集合的代表元素。
这样一来，一棵树就表示一个集合，一个个集合又构成了森林。
我们可以维护一个fa[ ]数组来记录这个森林，fa[x]存储的是x的父节点。

2.1 存储

代码实现

const int maxn=1e3+10;
int fa[maxn];

2.2 初始化

最初，每个节点都是一个集合，那它所在集合的代表就是它本身，即n棵1个点的树。
于是把每个点所在集合初始化为其自身（也就是让fa[i]=i）。
通常来说，这个步骤在每次使用该数据结构时只需要执行一次，无论何种实现方式，时间复杂度均为O(N)。

代码实现

const int maxn=1e3+10;
int fa[maxn];
void init(){
	for(int i=0;i<maxn;i++)fa[i]=i;
}

2.3 查询

查找元素所在的集合，即根节点（该节点所在集合的代表）。找爸爸
我们一般采用递归的方法来实现。
我们需要从该元素开始通过fa[ ]存储的值不断递归访问父节点，直至到达树根。
为了提高查询效率，我们一般采用路径压缩的方法进行优化。
（路径压缩的前提：不考虑树的具体形态）

代码实现

//1：非路径压缩
int findfa(int x){
	if(fa[x]==x)return x;//如果x是树根，则x就是集合的代表
	return findfa(fa[x]);//否则递归访问fa[x]直至根节点
}

//2：路径压缩
int findfa(int x){
	if(fa[x]==x)return x;//如果x是树根，则x就是集合的代表，否则递归访问fa[x]直至根节点
	return fa[x]=findfa(fa[x]);//压缩路径
}

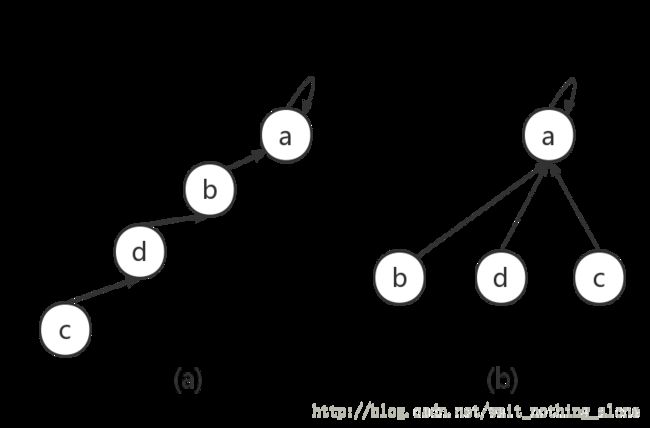
路径压缩图解

2.4 合并

将两个元素所在的集合合并为一个集合（或把两个集合合并为一个大集合）。
通常来说，合并之前，应先判断两个元素是否属于同一集合，这可用上面的“查找”操作实现。

void uni(int x,int y){
	int fax=findfa(x),fay=findfa(y);
	if(fax==fay)return ;
	fa[fax]=fay;
}

3 解题报告

3.1 POJ - 1611 The Suspects

Time Limit: 1000MS
Memory Limit: 20000K
Total Submissions: 23337
Accepted: 11345

Description
Severe acute respiratory syndrome (SARS), an atypical pneumonia of unknown aetiology, was recognized as a global threat in mid-March 2003. To minimize transmission to others, the best strategy is to separate the suspects from others.
In the Not-Spreading-Your-Sickness University (NSYSU), there are many student groups. Students in the same group intercommunicate with each other frequently, and a student may join several groups. To prevent the possible transmissions of SARS, the NSYSU collects the member lists of all student groups, and makes the following rule in their standard operation procedure (SOP).
Once a member in a group is a suspect, all members in the group are suspects.
However, they find that it is not easy to identify all the suspects when a student is recognized as a suspect. Your job is to write a program which finds all the suspects.

Input
The input file contains several cases. Each test case begins with two integers n and m in a line, where n is the number of students, and m is the number of groups. You may assume that 0 < n <= 30000 and 0 <= m <= 500. Every student is numbered by a unique integer between 0 and n−1, and initially student 0 is recognized as a suspect in all the cases. This line is followed by m member lists of the groups, one line per group. Each line begins with an integer k by itself representing the number of members in the group. Following the number of members, there are k integers representing the students in this group. All the integers in a line are separated by at least one space.
A case with n = 0 and m = 0 indicates the end of the input, and need not be processed.

Output
For each case, output the number of suspects in one line.

Sample Input
100 4
2 1 2
5 10 13 11 12 14
2 0 1
2 99 2
200 2
1 5
5 1 2 3 4 5
1 0
0 0

Sample Output
4
1
1

题目大意：
有一种病毒（SARS）和 0 ~ n-1 个同学，编号为 0 的同学为传染源（已感染SARS）。现有很多组学生，在同一个组的学生经常会接触，但是SARS是很容易传染的，只要组内有一位同学感染SARS，那么该组所有同学都被认为得了SARS。现要计算出有多少位学生感染SARS。

思路：
把同一组的同学合并在一起，最后遍历每个同学的“爸爸”，如果他的“爸爸”与编号为0的同学的“爸爸”一样，那么ans++，最后输出ans即可。

代码实现

#include
#include
using namespace std;
const int maxn=3e4+10;
int n,m;
int fa[maxn];
void init(){
	for(int i=0;i<maxn;i++){
		fa[i]=i;
	}
}

int findfa(int x){
	if(fa[x]==x)return x;
	return fa[x]=findfa(fa[x]);
}

void uni(int x,int y){
	int fax=findfa(x),fay=findfa(y);
	if(fax==fay)return;
	fa[fax]=fay;
}

int main(){
	while(scanf("%d%d",&n,&m)!=EOF){
		if(n==0&&m==0)break;
		init();
		int ans=0;
		for(int i=1;i<=m;i++){
			int mm;
			scanf("%d",&mm);
			if(mm>=1){
				int x,y;
				scanf("%d",&x);
				for(int j=2;j<=mm;j++){
					scanf("%d",&y);
					uni(x,y);
				}
			}
		}
		int ra=findfa(0);
		for(int i=0;i<n;i++){
			if(findfa(i)==ra)ans++;
		}
		cout<<ans<<endl;
	}
	return 0;
}

3.2 POJ - 2236 Wireless Network

Time Limit: 10000MS
Memory Limit: 65536K
Total Submissions: 47351
Accepted: 19432

Description
An earthquake takes place in Southeast Asia. The ACM (Asia Cooperated Medical team) have set up a wireless network with the lap computers, but an unexpected aftershock attacked, all computers in the network were all broken. The computers are repaired one by one, and the network gradually began to work again. Because of the hardware restricts, each computer can only directly communicate with the computers that are not farther than d meters from it. But every computer can be regarded as the intermediary of the communication between two other computers, that is to say computer A and computer B can communicate if computer A and computer B can communicate directly or there is a computer C that can communicate with both A and B.

In the process of repairing the network, workers can take two kinds of operations at every moment, repairing a computer, or testing if two computers can communicate. Your job is to answer all the testing operations.

Input
The first line contains two integers N and d (1 <= N <= 1001, 0 <= d <= 20000). Here N is the number of computers, which are numbered from 1 to N, and D is the maximum distance two computers can communicate directly. In the next N lines, each contains two integers xi, yi (0 <= xi, yi <= 10000), which is the coordinate of N computers. From the (N+1)-th line to the end of input, there are operations, which are carried out one by one. Each line contains an operation in one of following two formats:

1. “O p” (1 <= p <= N), which means repairing computer p.
2. “S p q” (1 <= p, q <= N), which means testing whether computer p and q can communicate.

The input will not exceed 300000 lines.

Output
For each Testing operation, print “SUCCESS” if the two computers can communicate, or “FAIL” if not.

Sample Input
4 1
0 1
0 2
0 3
0 4
O 1
O 2
O 4
S 1 4
O 3
S 1 4

Sample Output
FAIL莫名被坑，把fail看成fall，WSL
SUCCESS

题目大意：
有一个计算机网络的所有线路都坏了，网络中有n台计算机，现在你可以做两种操作，修理（O）和检测两台计算机是否连通（S），只有修理好的计算机才能连通。连通有个规则，两台计算机的距离不能超过给定的最大距离D（一开始会给你n台计算机的坐标）。检测的时候输出两台计算机是否能连通。

思路：
把已经修理的电脑且相距小于等于d的电脑相连，查询时，如果两台电脑在同一个集合里，就输出SUCCESS，否则，输出FAIL。

代码实现

#include
#include
#include
#include
using namespace std;
const int maxn=1e3+10;
int n,m;
double d;
int fa[maxn];
bool v[maxn];

struct node {
	double x,y;
} pc[maxn];

void init() {
	for(int i=0; i<maxn; i++) {
		fa[i]=i;v[i]=0;
	}
}

int findfa(int x) {
	if(fa[x]==x)return x;
	return fa[x]=findfa(fa[x]);
}

void uni(int x,int y) {
	int fax=findfa(x),fay=findfa(y);
	if(fax==fay)return;
	fa[fax]=fay;
}

double get_r(node a,node b){
	return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

int main() {
	scanf("%d%lf",&n,&d);
	init();
	for(int i=1; i<=n; i++)
		scanf("%lf%lf",&pc[i].x,&pc[i].y);
	++n;
	char op;int x,y;
	while(scanf("%c",&op)!=EOF){
		if(op=='O'){
			scanf("%d",&x);
			v[x]=1;
			for(int i=1;i<=n;i++){
				if(get_r(pc[x],pc[i])<=d&&i!=x&&v[i]){
					uni(x,i);
				}
			}
		}
		else if(op=='S'){
			scanf("%d%d",&x,&y);
			int fax=findfa(x),fay=findfa(y);
			if(fax==fay)cout<<"SUCCESS"<<endl;
			else cout<<"FAIL"<<endl;
		}
	}
	return 0;
}

3.3 HDU - 1213 How Many Tables

Time Limit: 2000/1000 MS (Java/Others)
Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 56817
Accepted Submission(s): 28316

Problem Description
Today is Ignatius’ birthday. He invites a lot of friends. Now it’s dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.

One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.

For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.

Input
The input starts with an integer T(1<=T<=25) which indicate the number of test cases. Then T test cases follow. Each test case starts with two integers N and M(1<=N,M<=1000). N indicates the number of friends, the friends are marked from 1 to N. Then M lines follow. Each line consists of two integers A and B(A!=B), that means friend A and friend B know each other. There will be a blank line between two cases.

Output
For each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.

Sample Input
2
5 3
1 2
2 3
4 5

5 1
2 5

Sample Output
2
4

题目大意：
今天是Ignatius的生日，他邀请了许多朋友。现在是吃晚饭的时间，Ignatius想知道他至少需要准备多少桌。必须注意的是，并非所有的朋友都相互认识对方，有的人不愿意和陌生人坐在一桌。针对此问题的一个重要的规则是，如果我告诉你A知道B，B知道C，这意味着，A和C认识对方，这样他们就可以留在一个桌子。但是如果我告诉你，A知道B，B知道C，D知道E，那么ABC可以坐在一起，DE就得另外再坐一桌了。你的任务是请根据输入的朋友之间的关系，帮助Ignatius求出需要安排多少桌。

思路：
求集合的数量，即如果fa[x]=x，ans++，最后输出ans。

代码实现

#include
#include
#include
#include
using namespace std;
const int maxn=1e3+10;
int n,m;
int fa[maxn];

void init() {
	for(int i=0; i<maxn; i++) {
		fa[i]=i;
	}
}

int findfa(int x) {
	if(fa[x]==x)return x;
	return fa[x]=findfa(fa[x]);
}

void uni(int x,int y) {
	int fax=findfa(x),fay=findfa(y);
	if(fax==fay)return;
	fa[fay]=fax;
}

int main() {
	int t;
	scanf("%d",&t);
	for(int Case=1;Case<=t;Case++){
		init();
		scanf("%d%d",&n,&m);
		for(int i=1;i<=m;i++){
			int x,y;
			scanf("%d%d",&x,&y);
			uni(x,y);
		}
		int ans=0;
		for(int i=1;i<=n;i++){
			int fax=findfa(i);
			if(fax==i)ans++;
		}
		cout<<ans<<endl;
	}
	return 0;
}

3.4 CodeForces - 1167C News Distribution

time limit per test 2 seconds
memory limit per test 256 megabytes
input standard input
output standard output

In some social network, there are n users communicating with each other in m groups of friends. Let’s analyze the process of distributing some news between users.

Initially, some user x receives the news from some source. Then he or she sends the news to his or her friends (two users are friends if there is at least one group such that both of them belong to this group). Friends continue sending the news to their friends, and so on. The process ends when there is no pair of friends such that one of them knows the news, and another one doesn’t know.

For each user x you have to determine what is the number of users that will know the news if initially only user x starts distributing it.

Input
The first line contains two integers n and m (1≤n,m≤5⋅10⁵) — the number of users and the number of groups of friends, respectively.

Then m lines follow, each describing a group of friends. The i-th line begins with integer ki (0≤ki≤n) — the number of users in the i-th group. Then ki distinct integers follow, denoting the users belonging to the i-th group.
It is guaranteed that ${\Sigma }_{i=1}^{m}ki<=5\ast 10^5$.

Output
Print n integers. The i-th integer should be equal to the number of users that will know the news if user i starts distributing it.

Example
Input
7 5
3 2 5 4
0
2 1 2
1 1
2 6 7

Output
4 4 1 4 4 2 2

题目大意：
在一些社交网络中，有 n 个用户在 m 组朋友圈中相互通信，让我们分析一下用户间信息传播的过程。一开始，x 个用户从一些渠道获取到信息，然后他把这条信息发给他的朋友（如果两个用户同在一个或多组朋友圈里面，他们就算是朋友）。朋友们又会把信息发送给他们的朋友，以此类推。 当没有一对像这样的朋友时（其中一个知道这条信息而另一个不知道这条信息），传播过程就结束了。对于每一个用户 x ，如果最初只有用户x开始发布消息，那么你需要输出知道该消息的用户数。

思路：
用一个sum[ ]数组存一下每个集合的大小，然后输出，就没了。

代码实现

#include
#include
#include
#include
using namespace std;
const int maxn=5e5+10;
int n,m;
int fa[maxn],sum[maxn];

void init() {
	for(int i=0; i<maxn; i++) {
		fa[i]=i;sum[i]=1;
	}
}

int findfa(int x) {
	if(fa[x]==x)return x;
	return fa[x]=findfa(fa[x]);
}

void uni(int x,int y) {
	int fax=findfa(x),fay=findfa(y);
	if(fax==fay)return;
	fa[fax]=fay;
	sum[fay]=sum[fax]+sum[fay];
}

int main() {
	scanf("%d%d",&n,&m);
	init();
	for(int i=1;i<=m;i++){
		int mm;
		scanf("%d",&mm);
		if(mm>=1){
			int x,y;
			scanf("%d",&x);
			for(int j=2;j<=mm;j++){
				scanf("%d",&y);
				uni(x,y);
			}
		}
	}
	for(int i=1;i<=n;i++){
		int fax=findfa(i);
		cout<<sum[fax]<<" ";
	}
	return 0;
}

3.5 POJ - 1456 Supermarket

Time Limit: 2000MS Memory Limit: 65536K
Total Submissions: 21881 Accepted: 9677

Description
A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σx∈Sellpx. An optimal selling schedule is a schedule with a maximum profit.
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80.

Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products.

Input
A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.

Output
For each set of products, the program prints on the standard output the profit of an optimal selling schedule for the set. Each result is printed from the beginning of a separate line.

Sample Input
4 50 2 10 1 20 2 30 1

7 20 1 2 1 10 3 100 2 8 2
5 20 50 10

Sample Output
80
185

题目大意：
超市里有N个商品. 第i个商品必须在保质期(第di天)之前卖掉, 若卖掉可让超市获得pi的利润，每天只能卖一个商品。现在你要让超市获得最大的利润。

思路：
贪心+并查集
先按价值降序排个序，然后从前往后遍历这n件商品，如果某商品的day的“爸爸”大于0，就说明符合要求，就把 它的“爸爸” 与 它的爸爸-1 合并，并把ans加上它对应的价值。

代码实现

#include
#include
#include
#include
using namespace std;
const int maxn=1e4+10;
int n,m;
int fa[maxn];

struct node{
	int val,day;
	bool operator < (const node& b)const {
		return b.val<val;
	}
} pd[maxn];

void init() {
	for(int i=0; i<maxn; i++) {
		fa[i]=i;
	}
}

int findfa(int x) {
	if(fa[x]==x)return x;
	return fa[x]=findfa(fa[x]);
}

void uni(int x,int y) {
	int fax=findfa(x),fay=findfa(y);
	if(fax==fay)return;
	fa[fax]=fay;
}


int main() {
	while(scanf("%d",&n)!=EOF) {
		init();
		for(int i=1; i<=n; i++)
			scanf("%d%d",&pd[i].val,&pd[i].day);
		sort(pd+1,pd+1+n);
		int ans=0;
		for(int i=1;i<=n;i++){
			int fax=findfa(pd[i].day);
			if(fax>0){
				ans+=pd[i].val;
				uni(fax,fax-1);
			}
		}
		cout<<ans<<endl;
	}
	return 0;
}

欢迎聚聚们批评指正>_<