2020牛客暑期多校训练营Enigmatic Partition(数学，二阶隔项差分)

Enigmatic Partition

题目描述

输入描述:

输出描述:

示例1

输入

3
5 7
7 9
1 9

输出

Case #1: 2
Case #2: 7
Case #3: 8

说明

题目大意

定义一个函数$f(n)$表示有多少满足以下条件的序列：

• $n=a_1+a_2+a_3+\cdots +a_m$，$m,i,a_i$均为正整数
• 对于任意的$i$，都有$a_i\le a_{i+1}\le a_i+1$
• $a_1+2=a_m$

现对于给出的每对$l,r$，要求$\sum _{i=l}^{r}f(i)$。

分析

看到数据范围就想这是道打表的题……

首先观察$f(n)$的条件。它是首尾差等于2并且相邻两个差最多为1的递增序列。
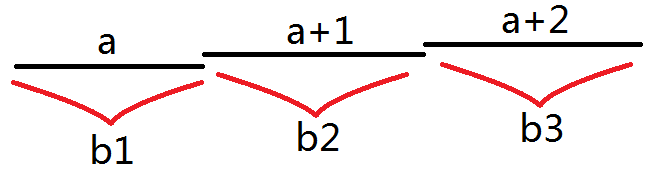
所以，对于每个数列，我们都可以分成3段。现在我们设第一段的数值为$a$，那么第二段是$a+1$，第三段是$a+2$，并且设每段的长度为$b_1,b_2,b_3$。显然，$b_1,b_2,b_3\ge 1$且$b_1+b_2+b_3=m$。如图

那么，根据题目，我们可以得出式子：
$a{b}_1+(a+1)b_2+(a+2)b_3=n$
$a(b_1+b_2+b_3)+b_2+2b_3=n$
$am+b_2+2b_3=n$
所以我们可以发现，对于一个$n$有$4$个未知数$a,m,b_2,b_3$。其中，$b_2,b_3$至少为$1$。

差分

当你需要求解区间加减求和时，可以考虑差分。
过程：在修改时，对于一个差分数组，我们在区间的首位加上修改值，末位减一的位置减去修改值，求前缀和就是最后经过修改的数组。
如果原数组是$a$，差分数组为$b$，则$a_i=b_i-b_{i-1}$。
接下来看差分的两个变式：

• 二阶差分 说白了就是差分套差分。如果要加上或减去一段有规律的数时，可以对差分数组再进行差分就可以了，这样可以把有规律的转化为同样的数值。例如加上$1,2,3,4,5,0$，我们对这段取差分为$1,1,1,1,1,-5$，那也就是对差分数组加上一段都为$1$的。然后继续差分，为$1,0,0,0,0,-6$，后面的0是补上去的。就可以对于这段快速修改了。
• 隔项差分 顾名思义，隔一项进行差分，例如加上$1,2,1,2,1,2$，那么隔项差分得$1,2,0,0,0,0,-1,-2$最后搞的时候隔项求前缀即可。

回到题目

然后我们看刚刚推的式子，发现$am$都是比较大的，难以考虑。因此不妨我们确定一个$a,m$，然后枚举$b_2,b_3$，并列表分析。
确定$a=1,m=6$，前几行往后$b_2$递增。

n	9	10	11	12	13	14	15	16	17	18
$b_3$=4							123333
$b_3$=3					112333	122333
$b_3$=2			111233	112233	122233
$b_3$=1	111123	111223	112223	122223
$f(n)$	1	1	2	2	2	1	1	0	0	0
差分	1	0	1	0	0	-1	0	-1	0	0
隔项	1	0	0	0	-1	-1	0	0	0	1
位置	am+3				(a+1)m+1	(a+1)m+2				(a+2)m
美化	----------	----------	----------	----------	----------	----------	----------	----------	----------	----------

所以我们在程序里只要枚举$a,m$，然后对于每个$a,m$，我们只要在上述位置进行加减，然后把差分后的数组搞回原来就可以了。

WA

注意枚举时只要枚举$a$为$m$的倍数，然后再带入，避免除法，一开始就是没有这样WA了一发……

代码

#include
#define ll long long
using namespace std;
const int MAXN=1e5+100;
ll f[MAXN<<2],pre[MAXN<<1];
int main()
{
    for(int m=3;m<MAXN;m++)
        for(int a=m;a<MAXN;a+=m)
            f[a+3]++,f[a+m+1]--,f[a+m+2]--,f[a+2*m]++;//在上述位置直接标记
    for(int i=3;i<MAXN;i++)
        f[i]+=f[i-2];//把隔位的差分搞回来
    for(int i=2;i<MAXN;i++)
        f[i]+=f[i-1];//再拆一层套娃
    pre[1]=f[1];
    for(int i=2;i<MAXN;i++)
        pre[i]=pre[i-1]+f[i];//前缀和快速求和
    int t,l,r;
    scanf("%d",&t);
    for(int _=1;_<=t;_++){
        scanf("%d%d",&l,&r);
        printf("Case #%d: %lld\n",_,pre[r]-pre[l-1]);
    }//直接输出答案
}

END

学到了差分太好用了~