高级数据结构——并查集基本操作

1.并查集概述：

a.什么叫并查集？
从字面意思理解，并就是合并，查就是查询，集就是集合的意思。
并查集是一种用于分离集合操作的抽象数据结构类型。它所处理的是集合之间的关系，即动态维护和处理集合元素之间复杂的关系，当给出两个元素的一个无序对(a,b)时，需要快速合并a和b所在的集合，这期间需要反复查找某个元素所在的集合。
b.简介：
在这种数据类型中，n个不同的元素被分为若干组，每组是一个集合，这种集合叫做分离集合。并查集支持查找一个元素所属的集合以及两个元素各自所属的集合的合并。

2.并查集中的基本操作：

a.初始化操作
首先我们要初始化一个并查集，一开始每一个元素相当于都是一个独立的集合。
father数组代表集合

//初始化并查集
for (int i = 1; i <= n; i++) {
	father[i] = i;
} 

b.查找操作：
由于规定同一个集合中只存在一个根节点，因此查找操作就是对给定的结点寻找其根节点的过程。实现的方式可以是递推或者递归，但是其思路都是一样的，即反复寻找父亲结点，直到找到根节点(即father[i] = i)
I.递推实现：

int findFather(int x) {  //函数返回元素x所在集合的根节点 
	while (x != father[x]) {	//如果不是根节点，继续循环 
		x = father[x];	//获得自己的父亲节点 
	}
	return x;
} 

II.递归实现：

int findFather1(int x) {
	if (x == father[x]) return x;	//如果找到了根节点 就返回节点编号x 
	else return findFather1(father[x]);	//否则，递归判断x的父亲结点是否是根节点 
} 

路径压缩查找方法：
上述所说并查集的查找方法是没有优化的，在极端情况下效率较低。比如给出的元素是1e5，查询次数在1e5那么每次都要花费1e5的时间查找，那么你就吃T了，怎么优化？

father[1] = 1;
father[2] = 1;
father[3] = 2;
father[4] = 3;

路径压缩后：

father[1] = 1;
father[2] = 1;
father[3] = 1;
father[4] = 1;

如图：

这样就相当于把当前查询结点的路径上所有结点的父亲结点指向根节点，查找的时候就不需要一直回溯去找父亲了，查询的复杂度为O(1)。
我们怎么实现？
在原有的find函数中，重新从x开始走一遍寻找根节点的过程，把路径上的所有结点的父亲改为根节点r

//路径压缩查找函数(递推) 
int find(int x) {
	int a = x; //由于下面的x会改变为根节点，因此把原先的x保存一下 
	while (x != father[x]) {  //寻找根节点 
		x = father[x];
	}
	//x存放的是根节点。把下面路径上的所有节点的父亲结点改为根节点 
	while (a != father[a]) {
		int z = a; //因为a要被father[a]覆盖，所以保存一下a的值 
		a = father[a]; //回溯父亲结点 
		father[z] = x; //将原来的父亲结点 改为根节点x 
	}
	return x;
} 

递归写法：

//路径压缩查找函数(递归)
int find(int v) {
	if (v == father[v]) return v; //找到根节点 
	else {
		int F = find(father[v]);  //递归寻找father[v]的根节点v 
		father[v] = F;	//将根节点F赋给father[v] 
		return F; //返回根节点 
	}
} 

整个并查集的查找操作大致就是这样了。

c.合并操作Union
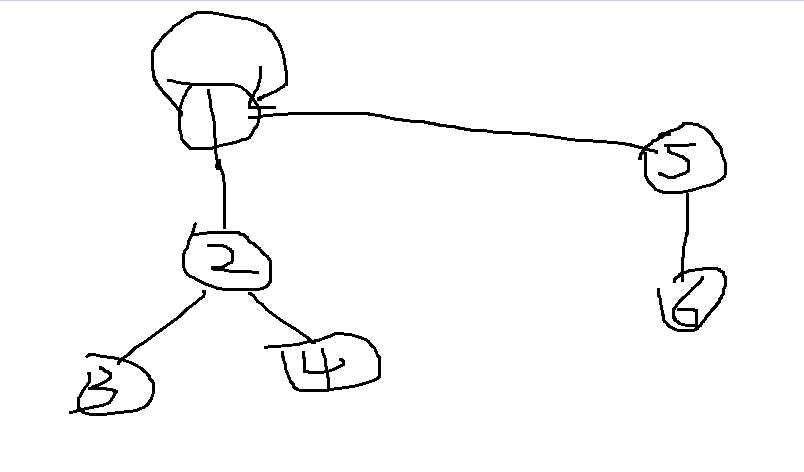
合并是把两个集合合并成一个集合，而合并的过程一般是把其中一个集合的根节点的父亲结点指向另一个集合的根节点。
主要分为两步走：
1.对于给定的两个元素a,b，判断他们是否在同一个集合，调用上面的查找函数，查找根节点是否一样。
2.合并两个集合，我们在1中通过find函数找到了两个根节点fa，fb那么只要把其中的一个节点的父亲结点指向另一个根节点即可。
father[fa] = fb即可。

//合并操作
void Union(int a, int b) {
	int faA = findFather(a);
	int faB = findFather(b);
	if (faA != faB) {
		father[faA] = faB;
	}
} 

3.入门并查集题目——亲戚：

题目链接
a.问题描述：

b.分析：
这是一道很直观可以发现使用并查集的一道题目。
有n个人，m个亲戚关系，我们可以看做有n个集合，判断是否有亲戚关系只要判断是否在同一集合，判断是否在同一集合可以判断这个点的根节点是否一样，主要用到并查集的查询，合并等操作。

c.AC_Code:

#include 
using namespace std;
const int maxn = 2e4 + 5;

int father[maxn];

void init(int n) {
	for (int i = 1; i <= n; i++) father[i] = i;
}

int find(int x) {
	if (x == father[x]) return x;
	else {
		int f = find(father[x]);
		father[x] = f;
		return f;
	}
}

void merge(int x, int y) {
	int fa = find(x);
	int fb = find(y);
	if (fa != fb) father[fa] = fb;
}

int main() {
	int n, m, q;
	scanf("%d%d%d", &n, &m, &q);
	init(n);
	while (m --) {
		int x, y;
		scanf("%d%d", &x, &y);
		if (find(x) != find(y)) {
			merge(x, y);
		}
	}
	while (q --) {
		int x, y;
		scanf("%d%d", &x, &y);
		if (father[find(x)] == father[find(y)]) printf("Yes\n");
		else printf("No\n");
	}
	return 0;
}