进制与整除
待到秋来九月八,我花开后百花杀
- 开局高能
- 真题
- 进制
- 天平秤重
- 尼姆堆
- 整除
- 公约和公倍
- 一步之遥
- 有理数
- 素数
开局高能
真题
【问题描述】 地产大亨Q先生临终的遗愿是:拿出100万元给X社区的居民抽奖,以稍慰藉心中愧疚。 麻烦的是,他有个很奇怪的要求:
100万元必须被正好分成若干份(不能剩余)。 每份必须是7的若干次方元。 比如:1元, 7元,49元,343元,…
相同金额的份数不能超过5份。
在满足上述要求的情况下,分成的份数越多越好!
请你帮忙计算一下,最多可以分为多少份?
首先当我们遇到这道题时,我们能想到最直接的办法就是:
100万中,总有一组适合由7或7的倍数的组合。
那么,我们就可以设置,从7的0次方到7次方(7的8次方会超过100万),每个会取0至5个不等,所有组合列出来,当有一个组合加起来为100万,则为所需要的。
此时,是一个组合重复问题。
解决方案:
排列组合https://blog.csdn.net/qq_40893595/article/details/106309401
然而这种方法,不仅编程难度大,即使编成,时间复杂度和空间复杂度也要大很多。
我们仔细想一想,为什么每个次方不能取5个以上,也就是说取少于6个,而如果把这看作7进制的算法,就懂了,如果每个次方允许取到6个,那么为了增加份数,高次方的完全可以拆开补全到低次方中。
正是因为,不能取5个以上,那么就意味着每个次方取的个数不会构成能够进一位的个数。
此时,我们的问题就简单了,这道题问的就是100万的7进制形式,和权的和。
public class strangeDonation {
public static void main(String[] args) {
String s = "";
int n = 1000000;
while(n != 0) {
s += n % 7;
n /= 7;
}
int sum = 0;
for (int i = 0; i < s.length(); i++) {
sum += s.charAt(i) - '0';// 把每个位的数加起来,就是答案了
}
System.out.println("转换成七进制后为:" + s);
System.out.println("最多有:" + sum + "份");
}
}
进制
在日常编程计算中非常常见,多见于二进制和十进制,由于思维的惯性,我们看到很多关于进制的题第一时间想到的是排列组合,但实际上,进制可以更加简化,例如上题。
天平秤重
【问题描述】用天平称重时,我们希望用尽可能少的砝码组合称出尽可能多的重量。
如果只有5个砝码,重量分别是1,3,9,27,81
则它们可以组合称出1到121之间任意整数重量(砝码允许放在左右两个盘中)。
本题目要求编程实现:对用户给定的重量,给出砝码组合方案。
例如:
用户输入:
5
程序输出:
9-3-1
用户输入:
19
程序输出:
27-9+1
要求程序输出的组合总是大数在前小数在后。
可以假设用户的输入的数字符合范围1~121。
方法一:
思路:
首先我们发现这题可以寻找规律,因此第一步想到的应该是递归法。
我们可以列出前几个查找规律,通过规律寻找解题方法,
1 1
2 3-1
3 3
4 3+1
5 9-3-1
从前五个可以发现,首先我们需要至少比所要表示数字大的砝码:
1、当出现相等时,直接输出。
2、当出现4之类的,比最大砝码的一半还要小的砝码时,则应该用比当前砝码小一级的砝码与之后的数字相加。
如:4 = 9/3+1
3、当出现5之类的,比最大砝码的一半还要大的砝码时,则应该用当前砝码减去多余的部分,此时多余部分需要用当前砝码减去当前所求所得。
如:5 = 9 - (3+1)
(3+1) = 9/3+1
注意:
第三种情况时,返回的数要求是去括号的反符号字符串,因此要再设置一个函数反转符号。
用递归实现:
public class balanceWeight {
static String Reve(String s) {
s = s.replace("+", "#");
s = s.replace("-", "+");
s = s.replace("#", "-");
return "-"+s;
}
public static String Balance(int n) {
int a = 1;
while(n > a)
a *= 3;
if(a == n)
return ""+a;
if(n <= a/2)
return a/3 + "+" + Balance(n - a/3);
return a + Reve(Balance(a - n));
}
public static void main(String[] args) {
for(int i = 1;i<100;i++) {
System.out.println(i+":"+Balance(i));
}
}
}
方法二:
思路:
我们发现砝码都是3的次方,因此将所求数字对3取模只会出现三种情况,为0,为1,为2,
1、当为1时,此砝码前必为“+”
2、当为2时,此砝码前必为“-”
3、当为0时,不用处理,在下一次循环时就会被带入。
但此循环构成的算式,前面会多出来一个符号,那么我们只需要裁取除第一位以外的字符串即可。
进制算法:
public class balanceWeight_1 {
public static String balance(int n) {
String s = "";
int q = 1;
while(n > 0) {
int shang = n / 3;
if(n % 3 == 1)
s = "+"+ q +s;
if(n % 3 == 2) {
shang++;
s = "-"+q+s;
}
n = shang;
q *= 3;
}
return s.substring(1);
}
public static void main(String[] args) {
for(int i = 1;i<100;i++) {
System.out.println(i+":"+balance(i));
}
}
}
尼姆堆
【问题描述】有3堆硬币,分别是3,4,5
二人轮流取硬币。
每人每次只能从某一堆上取任意数量。
不能弃权。
取到最后一枚硬币的为赢家。
求先取硬币一方有无必胜的招法。
思路:
根据数学家尼姆的说法,假设对于本题:
其二进制分别为:
011
100
101
——
010
对其整体异或之后的总数,其最高位的1所对应贡献者的数,所有贡献者都可以通过改变自身,使异或总数变成全0,改变的数即为题中取出后剩余的数量。
此为二进制的算法之一,二进制也是最广泛的考点之一,因其可以逻辑运算而被常考。
我们知道了尼姆的想法,现在我们需要让计算机也学会这个算法,但是计算机不知道如何通过最高位的1,找到其贡献者。
我们可以对异或后的总数与其所有数再次异或,所得到的数,我们会发现就是可以使抑或总数变为全0的数。
但,注意,如果不是贡献者,那么改变后的数将会大于改变前的,从一个堆中取一定量的数,不会使这个堆变得更大,只会更小,因此这种情况一定不是贡献者,排除。
程序实现:
public class nimPile {
static void Nim(int[] a) {
int sum = 0;
for(int i = 0;i<a.length;i++) {
sum ^= a[i];
}
if(sum == 0) {
System.out.println("必输");
}
for(int i = 0;i<a.length;i++) {
int x = sum ^ a[i];
if(x < a[i]) {
System.out.println(a[i]+"-->"+x);
}
}
}
public static void main(String[] args) {
int[] a = {3,4,5};
Nim(a);
}
}
整除
在编程中,数学算式和总结的快捷方程规律,也是提高编程效率的不二之选。
公约和公倍
怎样求最大公约数,最小公倍数?
思路:
众所周知的欧几里得算法,即辗转相除法。
再利用最小公倍数和最大公约数的关系式,求的最大公倍数。
public class ConventionsAndMultiples {
static int gcd(int a,int b) {
if(b == 0) {
return a;
}
return gcd(b , a % b);
}
static int lcm(int a, int b) {
return a * b / gcd(a,b);
}
public static void main(String[] args) {
System.out.println("最大公约数为:"+gcd(45,60));
System.out.println("最小公倍数为:"+lcm(60,45));
}
}
相关链接:
https://blog.csdn.net/qq_40893595/article/details/90547220
一步之遥
【问题描述】
从昏迷中醒来,小明发现自己被关在X星球的废矿车里。
矿车停在平直的废弃的轨道上。
他的面前是两个按钮,分别写着“F”和“B”。小明突然记起来,这两个按钮可以控制矿车在轨道上前进和后退。
按F,会前进97米。按B会后退127米。
透过昏暗的灯光,小明看到自己前方1米远正好有个监控探头。
他必须设法使得矿车正好停在摄像头的下方,才有机会争取同伴的援助。
或许,通过多次操作F和B可以办到。矿车上的动力已经不太足,黄色的警示灯在默默闪烁…
每次进行 F 或 B 操作都会消耗一定的能量。
小明飞快地计算,至少要多少次操作,才能把矿车准确地停在前方1米远的地方。请填写为了达成目标,最少需要操作的次数。
思路:
这里需要严谨的数学计算知识。
推导一个严谨的公式,实现函数。
从题中可以了解到,此题用方程抽象化,是一个二元一次不定方程:
问题转化为,解不定方程:
97x+127y = 1
根据欧几里得所得公式:
Ax + By = gcd(A,B)(最大公约数)
(不定方程)一定有解(特解)
推导
Ax + By = gcd(B,A%B)
(A/B* B + A%B) x + By =gcd(B,A%B)
B(A/B *x + y) +(A%B) *x =gcd(B,A%B)
B *x新 +(A%B)*y新 = gcd(B,A%B)
解得:
x = y新
y = x新 - A/B * y新
通过推导我们发现,这个公式可以根据递归的规律来解
public class OnePaceAway {
static int e_gcd(int A,int B,int[] xy) {
if(B == 0) {
xy[0] = 1;
xy[1] = 0;
return A;
}
int ans = e_gcd(B,A%B,xy);
int t = xy[0];
xy[0] = xy[1];
xy[1] = t - A/B * xy[0];
return ans;
}
public static void main(String[] args) {
int[] xy = new int[2];
int a = e_gcd(97,127,xy);
System.out.println(a);
System.out.println(xy[0]+" "+xy[1]);
}
}
有理数
【问题描述】如果求 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + … + 1/100 = ?
要求绝对精确,不能有误差。
思路:
计算机在对浮点数计算时,使用得是二进制计算,并且储存方式,也会影响浮点数的计算精度,因此浮点数计算不是绝对精确,例如:

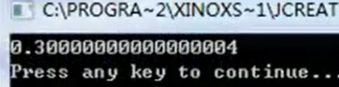

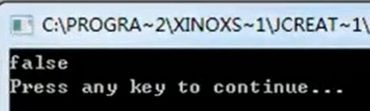
这种情况在一些金融行业内部是致命性的,因此我们不能直接使用浮点数计算。
浮点数在计算机中的储存:https://blog.csdn.net/qq_40893595/article/details/105149835
我们可以联想,在小学时,我们无法表示的有理数,可以用分数来表示,那么我们可以自己创建一个对象,面向对象编程,创造一个分数类,用以分数的计算,达到精准无误。
import java.math.BigInteger;
class Rati{
private BigInteger on = BigInteger.ZERO;
private BigInteger down = BigInteger.ONE;
private static BigInteger gcd(BigInteger a, BigInteger b) {
if(b.equals(BigInteger.ZERO))
return a;
return gcd(b,a.mod(b));
}
public Rati(long x) {
this(BigInteger.valueOf(x),BigInteger.ONE);
}
public Rati(long x,long y) {
this(BigInteger.valueOf(x),BigInteger.valueOf(y));
}
public Rati(BigInteger x) {
this(x,BigInteger.ONE);
}
public Rati(BigInteger x,BigInteger y) {
on = x;
down = y;
BigInteger g = gcd(x,y);
on = on.divide(g);
down = down.divide(g);
}
public Rati add(Rati other) {
return new Rati(on.multiply(other.down).add(other.on.multiply(down)),down.multiply(other.down));
}
public Rati subtract(Rati other) {
return new Rati(on.multiply(other.down).subtract(other.on.multiply(down)),down.multiply(other.down));
}
public Rati multiply(Rati other) {
return new Rati(on.multiply(other.on),down.multiply(other.down));
}
public Rati divide(Rati other) {
return new Rati(on.multiply(other.down),down.multiply(other.on));
}
public String toString() {
String s = on.toString();
if(down.equals(BigInteger.ONE)==false) {
s = s + "/" + down.toString();
}
return s;
}
}
public class rationalNumber {
public static void main(String[] args) {
System.out.println(new Rati(1,3).add(new Rati(1,3)));
}
}
素数
【问题描述】第1个素数是2,第2个素数是3,…
求第100002(十万零二)个素数
我们可以很轻松的通过计算机得到前100的素数,但我们如果想要获得更大数字的素数,计算机很有可能会发生溢出的情况导致数据出错。
素数本身的特质是有规律的,但根据其特质计算,会溢出,那么只能寻找其分布特点,但是它的分布也是分散的,并且当数字越大,越分散。
长期的寻找中,只有筛法,是最便捷的方法了。
思路:
找到范围内,最小的素数,将其倍数删去,再将指针下移,把下一个数一定是素数,再将其的倍数删去,直到指针到达最后,此时形成一个筛子,删去的做标记,未删去的就是素数,在用这个筛子,就可以筛选素数。
//筛法取素数
public class primeNumber {
public static void main(String[] args) {
int N = 1500 * 1000;
int x = 100002;
byte[] a = new byte[N];//筛子
for(int i = 2;i<N/2;i++) {
if(a[i] == 1)
continue;
for(int j = 2;j<=N/i;j++) {//筛子,1为合数
if(i * j < N)
a[i*j] = 1;
}
}
int m = 0;
for(int i = 2;i<N;i++) {
if(a[i] == 0) {
m++;
if(m == x) {
System.out.println("第"+m+"个:"+ i);
}
}
}
}
}
注意:这里制作筛子时,循环遍历只到N/2,原因是,大于N/2的数的倍数一定是大于N的,因此这些数是没有倍数的,没必要再去遍历。