07_数据降维,降维算法,主成分分析PCA,NMF,线性判别分析LDA
1、降维介绍
保证数据所具有的代表性特性或分布的情况下,将高维数据转化为低维数据。
聚类和分类都是无监督学习的典型任务,任务之间存在关联,比如某些高维数据的分类可以通过降维处理更好的获得。
降维过程可以被理解为数据集的组成成分进行分解(decomposition)的过程,因此sklearn为降维模块命名为decomposition。在对降维算法调用需要使用sklearn.decomposition模块

2、降维算法
转载:https://blog.csdn.net/bxg1065283526/article/details/80014481
(1)主成分分析(PCA)
主成分分析(Principal Component Analysis,PCA)是最常用的一种降维方法,通常用于高维数据集的探索与可视化,还可以用作数据压缩和预处理等。PCA可以把具有相关性的高维变量合成为线性无关的低维变量,称为主成分。主成分能够尽可能保留原始数据的信息。
其中需要理解的一些数学知识:
1、方差:是各个样本和样本均值的差的平方和的均值,用来度量一组数据的分散程度。

2、协方差:用于度量两个变量之间的线性相关性程度,若两个变量的协方差为0,则可认为二者线性无关。协方差矩阵则是由变量的协方差值构成的矩阵(对称阵)

3.特征向量:矩阵的特征向量是描述数据集结构的非零向量,并满足 如下公式:
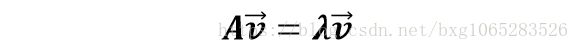
其中A是方阵,υ是特征向量,λ是特征值
算法原理: 矩阵的主成分就是其协方差矩阵对应的特征向量,按照对应的特征值大小进行排序,最大的特征值就是第一主成分,其次是第二主成分,以此类推。
使用sklearn.decomposition.PCA加载PCA进行降维,主要参数有:
n_components:指定主成分的个数,即降维后数据的维度
svd_solver :设置特征值分解的方法,默认为‘auto’,其他可选有 ‘full’,‘arpack’, ‘randomized’
实例:
已知鸢尾花数据是4维的, 共三类样本。使用PCA实现对鸢尾花 数据进行降维,实现在二维平面上的可视化。
#加载可视化的库
import matplotlib.pyplot as plt
#加载PCA算法包
from sklearn.decomposition import PCA
#加载鸢尾花数据集导入函数
from sklearn.datasets import load_iris
#以字典形式加载鸢尾花数据集
data = load_iris()
# 使用y表示数据集中的目标值,即类别
y = data.target
#使用X表示数据集中的标签
x = data.data
print(y)
print("------------------------------")
print(x)
print("==============================")
#加载PCA算法,设置降维后主成分数目为2
pca = PCA(n_components=2)
#对原始数据进行降维,保存在reduced_X中
reduce_X = pca.fit_transform(x)
print(reduce_X)
# 按类别对降维后的数据进行保存
# 第一类数据点
red_x,red_y = [],[]
# 第二类数据点
blue_x,blue_y = [],[]
# 第三类数据点
green_x,green_y=[],[]
for i in range(len(reduce_X)):
if y[i] == 0:
red_x.append(reduce_X[i][0])
red_y.append(reduce_X[i][0])
elif y[i] == 1:
blue_x.append(reduce_X[i][0])
blue_y.append(reduce_X[i][1])
else:
green_x.append(reduce_X[i][0])
green_y.append(reduce_X[i][1])
# 降维数据的可视化
plt.scatter(red_x,red_y,c='r',marker='x')
plt.scatter(blue_x,blue_y,c='b',marker='D')
plt.scatter(green_x,green_y,c='g',marker='.')
plt.show()
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
------------------------------
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
[5.7 3.8 1.7 0.3]
.......
[6.5 3. 5.2 2. ]
[6.2 3.4 5.4 2.3]
[5.9 3. 5.1 1.8]]
==============================
[[-2.68412563 0.31939725]
[-2.71414169 -0.17700123]
[-2.88899057 -0.14494943]
[-2.74534286 -0.31829898]
.....
[ 1.94410979 0.1875323 ]
[ 1.52716661 -0.37531698]
[ 1.76434572 0.07885885]
[ 1.90094161 0.11662796]
[ 1.39018886 -0.28266094]]
可以看出,降维后的数 据仍能够清晰地分成三类。 这样不仅能削减数据的维度, 降低分类任务的工作量,还 能保证分类的质量。
(2)非负矩阵分解(NMF)
非负矩阵分解(Non-negative Matrix Factorization ,NMF)是在矩阵中所有元素均为非负数约束条件之下的矩阵分解方法。
基本思路: 给定一个非负矩阵V,NMF能够找到一个非负矩阵W和一个非负矩阵H,使得矩阵W和H的乘积近似等于矩阵V中的值。并且有且仅有一个这样的分解,即满足存在型和唯一性。
![]()

w矩阵:基础图像矩阵,相当于从原矩阵V中抽取出来的特征
H矩阵:系数矩阵。
NMF能够广泛应用与图像分析,文本挖掘和语音处理等领域。
问题描述
给定矩阵V
给定矩阵![]() ,寻找非负矩阵
,寻找非负矩阵![]() 和非负矩阵
和非负矩阵![]() ,使得
,使得![]()
分解前后可理解为:原始矩阵V的列向量是对左矩阵W中所有列向量的加权和,而权重系数就是右矩阵对应列向量的元素,故称W为基矩阵,H为系数矩阵。一般情况下r的选择要比n小,即满足(m + n)r < mn。
这时用系数矩阵代替原始矩阵,就可以实现对原始矩阵进行降维,得到数据特征的降维矩阵,从而减少存储空间,减少计算机资源。
NMF实现原理
NMF求解问题实际上是一个最优化问题,利用乘性迭代的方法求解W和H,非负矩阵分解是一个NP问题。NMF题的目标函数有很多种,应用最广泛的就是欧几里得距离和KL散度。
在NMF的分解问题中,假设噪声矩阵为![]() ,那么有
,那么有
![]()
现在要找出合适的和使得最小。假设噪声服从不同的概率分布,通过最大似然函数会得到不同类型的目标函数。接下来会分别以噪声服从高斯分布和泊松分布来说明。

取对数后,得到对数似然函数为:

假设各数据点噪声的方差一样,那么接下来要使得对数似然函数取值最大,只需要下面目标函数值最小。

该损失函数为2范数损失函数,它是基于欧几里得距离的度量。又因为
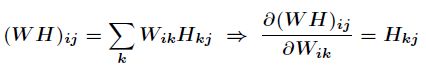
那么得到:

同理有:

接下来就可以使用梯度下降法进行迭代了。如下:

如果选取:

那么最终得到迭代式为:
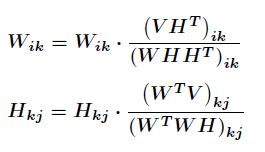
可看出这是乘性迭代规则,每一步都保证了结果为正数,一直迭代下去就会收敛,当然收敛性的证明省略。
(2)噪声服从泊松分布
若噪声为泊松噪声,那么得到损失函数为:

同样经过推导得到:

最后总结为:
矩阵分解优化目标: 最小化W矩阵H矩阵的乘积和原始矩阵之间的差别,目标函数如下:

基于KL散度的优化目标,损失函数如下:

具体使用:
在sklearn库中,可以使用sklearn.decomposition.NMF加载NMF算 法,主要参数有:
n_components:用于指定分解后矩阵的单个维度k;
init:W矩阵和H矩阵的初始化方式,默认为‘nndsvdar’
实例:NMF人脸数据特征提取
目标:已知Olivetti人脸数据共 400个,每个数据是64*64大小。由于NMF分解得到的W矩阵相当于从原始矩阵中提取的特征,那么就可以使用NMF对400个人脸数据进行特征提取。
通过设置k的大小,设置提取的 特征的数目。在本实验中设置k=6, 随后将提取的特征以图像的形式展示 出来。

3、PCA是什么
本质:PCA是一种分析、简化数据集的技术
目的:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
作用:可以削减回归分析或者聚类分析中特征的数量。
3.1、PCA语法
PCA(n_components=None)
将数据分解为较低维数空间
PCA.fit_transform(X)
X:numpy array格式的数据[n_samples,n_features]
返回值:转换后指定维度的array
3.2 PCA流程
1、初始化PCA,指定减少后的维度
2、调用fit_transform
例如对以下的numpy数组进行降维:
[[2,8,4,5],
[6,3,0,8],
[5,4,9,1]]
案例:
from sklearn.decomposition import PCA
def pca():
"""
主成分分析进行特征降维
:return: None
"""
pca = PCA(n_components=0.9)
data = pca.fit_transform([[2,8,4,5],[6,3,0,8],[5,4,9,1]])
print(data)
return None
if __name__ == "__main__":
pca()
输出结果为:
[[ 1.22879107e-15 3.82970843e+00]
[ 5.74456265e+00 -1.91485422e+00]
[-5.74456265e+00 -1.91485422e+00]]
4 其它降维方法
4.1 线性判别分析LDA
转载:
https://blog.csdn.net/mbx8x9u/article/details/78739908
LDA在模式识别领域(比如人脸识别,舰艇识别等图形图像识别领域)中有非常广泛的应用,因此我们有必要了解下它的算法原理。在学习LDA之前,有必要将其自然语言处理领域的LDA区别开来,在自然语言处理领域, LDA是隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),是一种处理文档的主题模型。本文只讨论线性判别分析,因此后面所有的LDA均指线性判别分析。
LDA思想
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的,这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”,如下图所示。 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。

可能还是有点抽象,先看看最简单的情况。
假设有两类数据,分别为红色和蓝色,如下图所示,这些数据特征是二维的,希望将这些数据投影到一维的一条直线,让每一种类别数据的投影点尽可能的接近,而红色和蓝色数据中心之间的距离尽可能的大。

LDA原理与流程:




LDA与PCA
LDA用于降维,和PCA有很多相同,也有很多不同的地方,因此值得好好的比较一下两者的降维异同点。
相同点:
1)两者均可以对数据进行降维。
2)两者在降维时均使用了矩阵特征分解的思想。
3)两者都假设数据符合高斯分布。
不同点
- LDA是有监督的降维方法,而PCA是无监督的降维方法
2)LDA降维最多降到类别数k-1的维数,而PCA没有这个限制。
3)LDA除了可以用于降维,还可以用于分类。
4)LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。这点可以从下图形象的看出,在某些数据分布下LDA比PCA降维较优。

当然,某些某些数据分布下PCA比LDA降维较优,如下图所示:

LDA小结
LDA算法既可以用来降维,又可以用来分类,但是目前来说,主要还是用于降维。在进行图像识别相关的数据分析时,LDA是一个有力的工具。下面总结下LDA算法的优缺点。
优点:
1)在降维过程中可以使用类别的先验知识经验,而像PCA这样的无监督学习则无法使用类别先验知识。
2)LDA在样本分类信息依赖均值而不是方差的时候,比PCA之类的算法较优。
缺点
1)LDA不适合对非高斯分布样本进行降维,PCA也有这个问题。
2)LDA降维最多降到类别数k-1的维数,如果我们降维的维度大于k-1,则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
3)LDA在样本分类信息依赖方面差而不是均值的时候,降维效果不好。
4)LDA可能过度拟合数据。

