基于Fuzzy Logic的人群疏散模型（考虑攻击者的情况）

基于Fuzzy Logic的人群疏散模型（考虑攻击者的情况）

1、介绍

因为要做的课题与人群疏散有关，老师给了几篇关于人群疏散的论文，其中有一篇是提出了一种模糊逻辑方法来研究人群疏散行为，同时考虑了有攻击者的情况（Modeling of Crowd Evacuation With Assailants via a Fuzzy Logic Approach）。我根据自己学习到的内容进行总结。

2、内容整理

2.1、背景

人群疏散是一项极具社会意义的研究，它的研究方法主要包括现实生活中的真实实验和基于模型的模拟实验。真实实验因为现实的限制，往往成本较大，很难完成，所以很多论文提出了一系列人群疏散模型来进行研究。
该论文提出的模型，主要有两个比较有特色的点，一个是考虑有攻击者情况下（大多数模型没有考虑这点），另一个是使用模糊逻辑的方法。
模糊逻辑具有对基于感知的信息进行操作和推理的能力，结合到人群疏散的具体背景中，它是这样理解的：人们在逃生过程中，得到的信息并不是“我距离逃生门10米，我前方有20个人”（这种叫做测量信息），而是“我距离逃生门很近了，但我前方人很多”（这种叫做感知信息），而模糊逻辑恰恰能够很好地处理这种感知信息。
语言模糊集的数量决定了模糊逻辑系统的准确性，比如将人的数量分为{很多，多，一般，少，很少}，就比分为{多，少}精确。

2.2、模型简述

2.2.1、空间表示

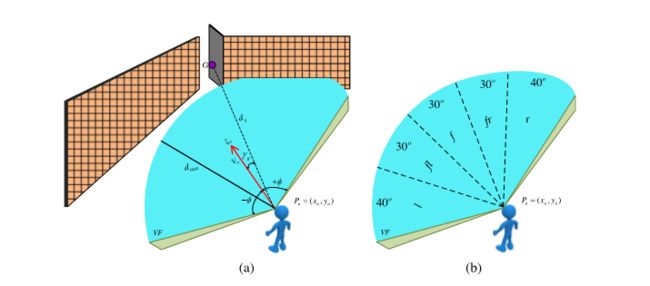
视觉是影响人在人群疏散过程中作判断的主要信息来源，个体的视野VF表示如图蓝色扇区，扇区可分五个部分，分别是左，左前，前，右前，右。
个体$n$的特征由所处位置$P_n$，方向${\xi }_n$，移动速度$V_n$组成。

2.2.2、模型结构

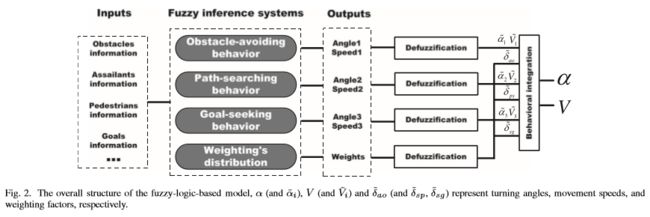
该模型由四个fuzzy inference system组成，它们分别用于描述obstacle-avoiding behavior（障碍物规避行为），path-searching behavior（路径搜索行为），goal-seeking behavior（目标寻找行为），weighting’s distribution principle（权重分配原则）。
前三个系统的输出信息是转角和运动速度的中间结构，最后一个系统是加权因子，用于确定某些周围条件下每种行为的重要性。

2.2.3、模型假设

• 假设一：所有个体不知道环境的全局信息，但是知道他视野中和目标点的信息。
• 假设二：个体可以在0.5s的犹豫时间中在任何两个预定义状态之间切换（似乎没怎么体现？）
• 假设三：攻击者的攻击范围即手臂长度0.75m。
• 假设四：未考虑行人的防御。
• 假设五：保安人员可以阻止攻击，但只体现为攻击持续时间。

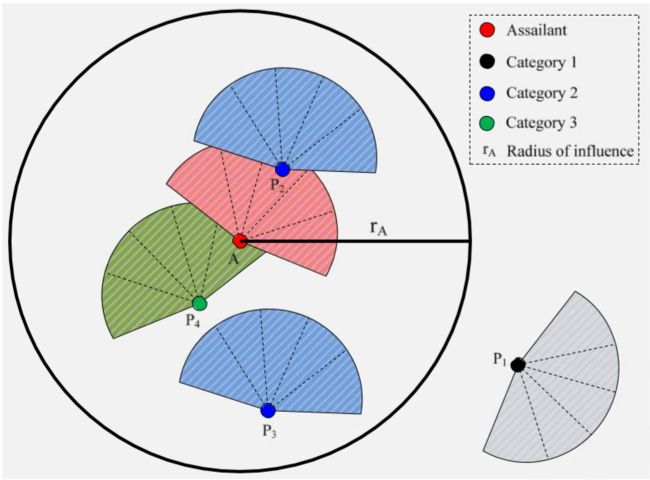
2.2.4、个体分类

个体	描述
攻击者	——
1类行人	不在攻击者的攻击范围内，如下图中P1
2类行人	在攻击者的攻击范围内，但看不到攻击者，如P2和P3
3类行人	行人可以看见攻击者，或者是行人曾看见过攻击者并且现在离他不远，如P4

2.2.5、三类行人之间转换

三类行人之间是可以进行转换的，具体公式如下：
$$P_{c1\to c2}=ϵexp[\frac{(d_{max}-d_{ap})}{{\kappa }_1}],d_{max}\le d_{ap}\le r_A$$ $$P_{c2\to c3}=(1-ϵ)exp[\frac{(2r_p-d_{ap})}{{\kappa }_2}],2r_p\le d_{ap}\le d_{max}$$ $$P_{c3\to c2}=1-ϵexp[\frac{(2r_p-d_{ap})}{{\kappa }_3}],2r_p\le d_{ap}\le d_{max}$$ $$P_{c2\to c1}=P_{c1\to c3}=P_{c3\to c1}=0$$ $$\sum _{i=1}^3{P}_{c1\to ci}=\sum _{i=1}^3{P}_{c2\to ci}=\sum _{i=1}^3{P}_{c3\to ci}=1$$ 其中$d_{ap}$表示行人和攻击者之间的距离，$d_{max}$表示视野扇区的半径，$r_A$表示攻击者的攻击范围，$r_p$表示行人在三维环境表示下的半径，${\kappa }_1$、${\kappa }_2$、${\kappa }_3$是常量，分别为2、8、1。

2.3、模型详述

2.3.1、The Local Obstacle-Avoiding Behavior

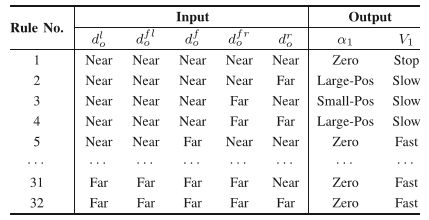
该行为指导行人避开障碍物，可以总结为如下公式：
$$\left[\begin{array}{c}{\alpha }_1\\ V_1\end{array}\right]=R_0(d_o^l,d_o^{fl},d_o^f,d_o^{fr},d_o^r)$$ 公式的输出${\alpha }_1$、$V_1$为行人经过该行为进行决策后的转角和移速，输入$d_o^{\ast }$ $\ast \in \{l,fl,f,fr,r\}$表示行人与各个扇区中最近障碍物的距离。$R_0$规则如下图所示：

2.3.2、The Regional Path-Searching Behavior

该行为驱使行人选择最安全的路径，它所根据的是每个扇区的Negative energy（负能量，$N{E}^{\ast }$），而$N{E}^{\ast }$是由障碍物的影响（$O{I}^{\ast }$）和碰撞风险（$C{R}^{\ast }$）决定的。
$$O{I}_i^{\ast }=R_1({\varphi }_{oi}^{\ast },d_{oi}^{\ast })$$ $$O{I}^{\ast }=\sum _{i\in S^{\ast }}O{I}_i^{\ast }$$ $O{I}^{\ast }$表示的是整个扇区的障碍物影响，$O{I}_i^{\ast }$经过$O{I}_i^{\ast }$去模糊化得到，$i$表示在扇区$S^{\ast }$中的障碍物编号。
${\varphi }_{oi}^{\ast }$表示障碍物所占视角，$d_{oi}^{\ast }$表示障碍物距离行人的最近距离，$R_1$规则表示为：${\varphi }_{oi}^{\ast }$越大，$d_{oi}^{\ast }$越近，$O{I}^{\ast }$越大。$$C{R}_j^{\ast }=R_2(d_{pj}^{\ast },V_j^{\ast },{\theta }_{pj}^{\ast })$$ $$C{R}^{\ast }=\sum _{j\in S^{\ast }}C{R}_j^{\ast }$$ $C{R}^{\ast }$表示的是整个扇区的碰撞风险，$C{R}_j^{\ast }$经过$C{R}_j^{\ast }$去模糊化得到，$j$表示在扇区$S^{\ast }$中的行人编号。
$d_{pj}^{\ast }$表示正在移动的行人j距离决策者的距离，$V_j^{\ast }$行人$j$的移动速度，${\theta }_{pj}^{\ast }$表示行人$j$移动方向和决策者之间的夹角，$R_2$规则表示为：远处正对的行人$j$高速移动，则$C{R}_j^{\ast }$较小。
$$N{E}^{\ast }=k_{\omega }\cdot O{I}^{\ast }+(1-k_{\omega })\cdot C{R}^{\ast }$$ $$\overline{N{E}^{\ast }}=\frac{max\{NE\}-N{E}^{\ast }}{max\{NE\}-min\{NE\}}$$ $$\left[\begin{array}{c}{\alpha }_2\\ V_2\end{array}\right]=R_3(\overline{N{E}^l},\overline{N{E}^{fl}},\overline{N{E}^f},\overline{N{E}^{fr}},\overline{N{E}^r})$$ $k_{\omega }$系数决定$O{I}^{\ast }$和$C{R}^{\ast }$的比重，$\overline{N{E}^{\ast }}$是$N{E}^{\ast }$经过归一化处理得到的结果，$R_3$规则与$R_0$规则相似，只不过把$R_0$中的$d_o^{\ast }$换为$\overline{N{E}^{\ast }}$。

2.3.3、The Goal-Seeking Behavior

该行为驱使行人向目标点移动，其公式如下：
$$\left[\begin{array}{c}{\alpha }_3\\ V_3\end{array}\right]=R_4({\gamma }_g,d_g)$$${\gamma }_g$表示的是目标角度，$d_g$表示的是目标距离，规则$R_4$如下：

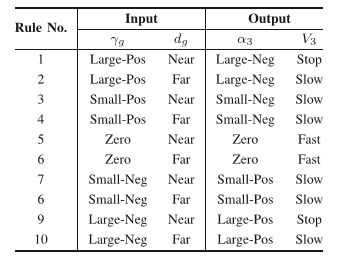
2.3.4、Integration of Multiple Behaviors

该行为用于对以上三种行为进行加权平均，其方法如下：$$\{\begin{array}{l}\alpha =\frac{{\tilde{\delta }}_{ao}\cdot {\tilde{\alpha }}_1+{\tilde{\delta }}_{sp}\cdot {\tilde{\alpha }}_2+{\tilde{\delta }}_{sg}\cdot {\tilde{\alpha }}_3}{{\tilde{\delta }}_{ao}+{\tilde{\delta }}_{sp}+{\tilde{\delta }}_{sg}}\\ V=\frac{{\tilde{\delta }}_{ao}\cdot {\tilde{V}}_1+{\tilde{\delta }}_{sp}\cdot {\tilde{V}}_2+{\tilde{\delta }}_{sg}\cdot {\tilde{V}}_3}{{\tilde{\delta }}_{ao}+{\tilde{\delta }}_{sp}+{\tilde{\delta }}_{sg}}\end{array}$$ $\stackrel{~}{}$ 表示对应模糊集的清晰值，加权因子${\delta }_{ao}$、${\delta }_{sp}$、${\delta }_{sg}$通过以下方法计算：$$\left[\begin{array}{c}{\delta }_{ao}\\ {\delta }_{sp}\\ {\delta }_{sg}\end{array}\right]=R_5(d_o^{\ast },\overline{N{E}^f},d_g)$$$R_5$规则如下：

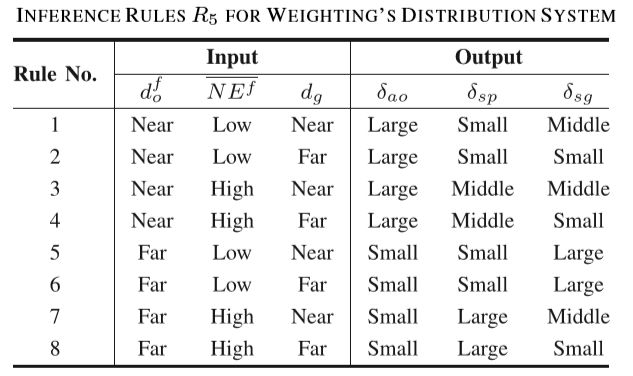
2.3.5、三类行人模型

因为三类行人的描述定义不同，他们对前三种behavior的使用也有所不同，具体：
1类行人可以直接使用；
2类行人因为察觉到危险的存在，会加快速度，所以他经过Path-Searching Behavior产生的$V_2$要经过修改：$V_2^{\prime }=(1-k_p)\cdot V_2+k_p\cdot V_{max}$，$k_p\in [0,1]$反映紧急程度，使速度有所提升但不超过最大速度；
3类行人因为攻击者影响Path-Searching，带来更多碰撞风险，所以CR需要重新定义：$$C{R}^{\ast }=\sum _{j\in S^{\ast }}C{R}_j^{\ast }+k_c\cdot \sum _{l\in S^{\ast }}C{R}_l^{\ast }$$公式的前半部分与原公式一致，后半部分表示攻击者带来的碰撞风险，其中$l$表示扇区$S^{\ast }$中的攻击者，速度也要进行修改：$V_2^{\prime \prime }=(1-k_p^{\prime })\cdot V_2+k_p^{\prime }\cdot V_{max}$，$k_p^{\prime }$通常比$k_p$大。

2.3.6、攻击者模型

攻击者的动态过程：首先攻击者扫描视野，选择候选对象，然后以适当的移动速度和方向跟踪选择的对象，同时避免与障碍物碰撞。最后当选定的对象受到攻击时，攻击者将继续前进到下一个候选对象处。直到所有物体都受到攻击和撤离为止。
攻击者的Local obstacle-avoiding behavior和行人相似。攻击者会根据行人的分布通过某种策略来选择道路，有三种简单的策略：选择最近的行人，选择最外围的行人，选择最中心的行人；也有复杂的策略：先选择吸引力最大的扇区，然后根据简单策略再选择具体的行人。
先来看简单的策略，除了选择最近的行人外，模型提供了peripherality（外围性）的概念来判断行人是位于人群的边缘还是中心，peripherality的大小等于$P_n$的长度。$$P_i=\frac{1}{|G|}\sum _{n\in G}\widehat{d_n},G=\{n\in V{F}_A;n\ne i\}$$$n$是位于视野中的行人（除了$i$），所以三种简单策略与以下三条公式对应：$$d_{min}=\underset{n\in T}{\min }||d_n||;T=\{n\in V{F}_A\}$$ $$P_{max}=\underset{n\in T}{\max }||P_n||;T=\{n\in V{F}_A\}$$ $$P_{min}=\underset{n\in T}{\min }||P_n||;T=\{n\in V{F}_A\}$$再看复杂的策略，扇区的吸引力被如下定义$$A^{\ast }=\frac{360\cdot N^{\ast }}{\pi \cdot {\theta }^{\ast }\cdot d_{max}^2}\cdot \sum _{j\in S^{\ast }}{e}^{-\frac{{\tilde{d}}_{aj}^{\ast }}{k_a}}$$其中，$N^{\ast }$表示扇区$S^{\ast }$中的行人数量，${\theta }^{\ast }$表示扇区$S^{\ast }$的中心角，$\widetilde{d_{aj}^{\ast }}$表示攻击者和行人$j$之间的距离，$k_a$是一个常量，反映距离对吸引力的影响。可以看出，行人数量越多，距离越近，则吸引力越大。
在选择对象后，攻击者按与行人相似的goal-seeking behavior（把$R_5$规则中的$\overline{N{E}^{\ast }}$替换为${\overline{A}}^{\ast }$）行动。
具体这个攻击者模型我没理解透（攻击者的searching-path是怎样的？攻击者的转向和移速也是通过三种behavior加权得到的吗？）

2.4、实验模拟

2.4.1、circuity现象

这是一种在模拟实验中发现的现象，它指出在遇袭，行人会优先选择相对安全的区域逃跑，而非直接出口。

2.4.2、实验数据

论文在这个模型的基础上做了几个实验，但不是特别具体（或者我没怎么理解？），以下贴出经实验得出的数据。

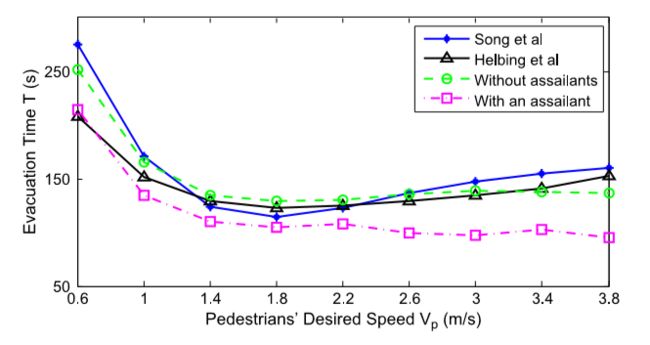
图对比了在有无攻击者的情况下，行人速度和疏散时间的关系。实验指出在有攻击者的情况下，疏散时间会下降，这是因为有些行人在遇袭之后倒下，不需要疏散时间了，所以疏散时间下降，但是行人倒下之后会成为障碍物，以及出现了circuity现象，故疏散时间也不会大幅度下降。

图反映了安全出口宽度对疏散时间和被攻击人数的影响，实验指出宽度增大，时间和人数都会下降，但是增大到饱和状态后，宽度继续增大，时间和人数就不会有明显的下降了。这个实验可以帮助场馆设计师在规划人群疏散问题时的参数设置。

图反映了行人速度和被攻击人数的关系，实验表明速度的提高将在一定程度上帮助减少被攻击的行人数量，但这并不是说速度越快越好。

3、总结

模糊逻辑方法的主要优点在于它能够在建模过程中充分利用基于感知的信息，此外考虑到人类在建模过程中的经验和知识所提出的模型，可以现实地模拟和预测人群疏散问题。