数据结构之线段树

线段树

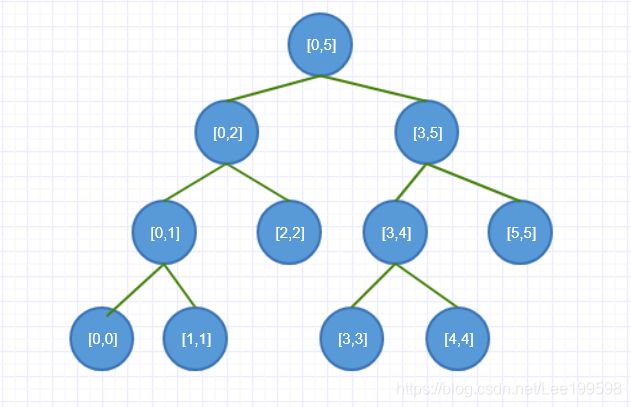
        线段树是一种高级数据结构，也是一种平衡二叉树。树的结点的值是对一段区间内操作后得到的值。这个操作可以是对某段区间进行求和、求积、求最大值、求最小值等等，且父结点存储的区间刚好包括两个子结点存储的区间。

如下所示：

                                   

 

为了便于理解，下面以对区间进行求和作为例子，我把这种线段树称为求和线段树，因为它的每一个结点是对一段区间求和。

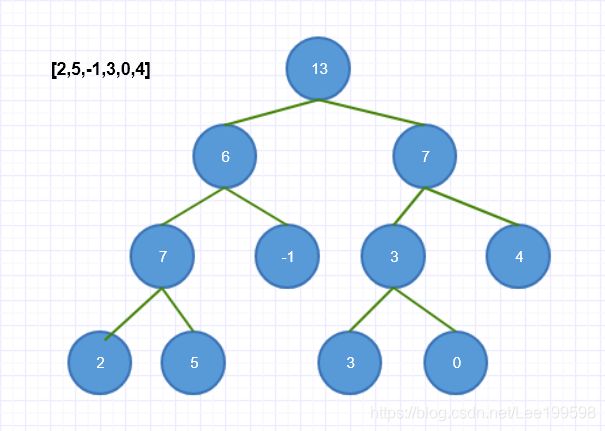
假设有一段数组[2,5,-1,3,0,4]；以求和线段树存储。则可表示如下：

                                  

理解了线段树的逻辑结构后就可以思考怎么在计算机中存储一棵线段树。由于线段树是一棵完全二叉树，所以可以选择使用数组进行存储。我们可以把上面的完全二叉树看作是一个满二叉树，空余地方以空结点补全。我们知道，满二叉树中结点的个数和高度的关系为：；n为结点总数，h为树的高度。可以通过推算得出：满二叉树每增加一层，其结点个数大概增加了一半。因此假设原数组长度为p，则用于保存其对应线段树的数组长度为4*p。

下面来介绍几个在重要的方法：至于下面方法，希望各位能够理解并记住。

//求当前结点的父结点在数组中的索引
int parentTreeIndex(int treeIndex){
    return (treeIndex-1)/2;
}

//求当前结点的左孩子结点的索引
int leftTreeIndex(int treeIndex){
    return treeIndex*2+1;
}

//求当前结点的右孩子结点的索引
int rightTreeIndex(int treeIndex){
    return treeIndex*2+2;
}

下面就来思考怎么通过一个数组实现一棵用数组存储的求和线段树。

通过前面的介绍我们知道，求和线段树上的每一个父亲结点所表示的区间都刚好包括了其两个子结点的区间，因此其父亲结点上的值就可以表示为两个子结点的值的和，没有子结点则其表示的区间长度为1。因此可以利用递归来实现我们的线段树，其递归结束的条件就是当前结点没有子结点，其值就是原数组元素的值。

//为容易理解这里假设保存的是Integer类型
public class SegmentTree{
    private E[] data;  //存储原数组元素的数组
    private E[] tree;  //用于表示线段树的数组

    public SegmentTree(Integer[] arr){
        data = (E[])new Object[arr.length];
        tree = (E[])new Object[arr.length*4];
        for(int i=0;i

理解了线段树的构建后下面就可以来实现线段树的另一种十分重要的操作了，查询某个区间。

以上面图形作为例子：当要查询[0,4]这个区间的和时，我们只需要知道[0,2]和[3,4]这两个结点即可，我们还知道对于二叉树的查找操作其时间复杂度为，其效率是很高的，这就是我们对于区间进行操作选择构建这种线段树的原因所在。

//查找原数组[queryL,queryR]区间的和
public E query(int queryL,int queryR){
    return query(0,0,data.length-1,queryL,queryR);
}

private E query(int treeIndex,int left,int right,int queryL,int queryR){
    int leftTree = leftTreeIndex(treeIndex);
    int rightTree = rightTreeIndex(treeIndex);
    int mid = leftTree + (right-left)/2;
    if(queryL>mid){ //要查询的区间在当前结点的右子树上
        return query(rightTree,mid+1,right,queryL,queryR);
    }
    if(queryR<=mid){ //要查询的区间在当前结点的左子树上
        return query(leftTree,left,mid,queryL,queryR);
    }
    //queryL