隐马尔可夫模型hidden Markov model

本文是《统计学习方法》李航著学习笔记。
为了叙述方便，将hidden Markov model简称HMM。HMM是一种用于标注问题的生成模型，模型工作过程：“隐藏的马尔科夫链”随机生成“不可观测的状态序列”，“每个状态”生成“一个观测”，从而得“观测序列”。在标注问题中，给定“最终的观测序列”，预测其对应的“状态序列”，也称为“标记序列”。可以把整个过程想象成一个网络层，各个状态点和观测点表示网络中的结点。

下面的叙述中主要涉及：
（a）介绍HMM的构成，包括初始状态概率、状态转移概率、观测概率；
（b）在给定模型和观测序列情况下，计算该观测序列出现的概率；
（c）在给定观测序列的情况下，以该观测序列出现概率最大为目标，利用极大似然或者EM算法计算模型参数，就是模型学习过程；
（d）在给定模型和观测序列的情况下，以状态序列的条件概率最大为目标，预测该观测序列对应的状态序列。
其中，（c）在状态序列未知情况下，需要利用EM算法迭代求解HMM参数时，就是以（b）为理论基础实施计算的。

HMM的构成

记HMM的数学表示为 λ ，它由初始概率分布 π ，状态转移概率分布 A 和观测概率分布 B 确定，即 λ=(A,B,π) 。

为了给出 λ 的具体数学表示，设所有可能的状态的集合为

Q={q1,q2,⋯,qN}

所有的观测的集合为

V={v1,v2,⋯,vM}

考虑长度为 T 的状态序列 I=(i1,i2,⋯,iT) ，其对应的观测序列 O=(o1,o2,⋯,oT) ，其中对于 k=1,2,⋯,T ， ik 取自 Q ， ok 取自 V ，则

初始状态概率向量π=(πi)，πi=P(i1=qi)状态转移概率矩阵A=[aij]N×N，aij=P(it+1=qj|it=qi)观测概率矩阵B=[bj(k)]N×M，bj(k)=P(ot=vk|it=qj)

观测序列的生成：
输入：HMM λ=(A,B,π) ，观测序列长度 T
输出：观测序列 O=(o1,o2,⋯,oT)
（1）t=1，由初始状态概率向量 π 产生状态 i1
（2）按照状态 it 的观测概率矩阵 B 中的 bit(k) 生成 ot
（3）按照状态 it 的状态转移概率矩阵 A 中的 aitit+1 产生状态 it+1
（4）置 t=t+1 ； if：t<T，turn：(2)；else：stop
即 i1→o1→i2→o2⋯→iT→oT ；这里需要注意，状态序列与观测序列的生成过程满足齐次马尔科夫性和观测独立性假设。

观测序列概率计算

给定HMM参数，可以通过直接法、前向算法和后向算法计算观测序列的概率。
（一）直接法：利用联合分布和边缘分布的关系，对状态序列进行遍历求和，只是理论上可行，计算量在 O(TNT) 阶。
（二）前向算法：根据前向概率向后递推求观测序列概率
前向概率：给定HMM参数 λ=(A,B,π) ，定义到时刻 t 部分观测序列为 o1,o2,⋯,ot ，且此时状态 it=qi 的概率为前向概率：

αt(i)=P(o1,o2,⋯,ot,it=qi|λ)

观测序列概率的前向算法：
输入：HMM λ=(A,B,π) ，观测序列 O
输出：观测序列概率 P(O|λ)
（1）初始前向概率

α1(i)=P(o1,i1=qi|λ)=πibi(o1)，i=1,2,⋯,N

（2）向后递推

αt+1(i)=P(o1,o2,⋯,ot+1,it+1=qi|λ)=∑j=1N[P(o1,o2,⋯,ot,it=qj|λ)aji]bi(ot+1)=∑j=1N[αt(j)aji]bi(ot+1)

（3）整体观测序列

P(O|λ)=∑i=1NP(o1,o2,⋯,oT,iT=qi|λ)=∑i=1NαT(i)

即， 在计算 αt+1(i) 时，不关注 t 时刻的 it 处于哪个状态，而 αt(i) 中包含 it=qj 的状态约束，要想通过 αt(i) 递推得 αt+1(i) ，必须遍历所以状态，去掉某个状态 qj 的影响。可类似看作网络层中，后一层每个节点的计算，需要用到前一层的每个节点。该算法的计算量是 O(N2T) 。

（三）后向算法：根据后向概率向前递推求观测序列概率
后向概率：给定HMM参数 λ=(A,B,π) ，定义在时刻 t 状态为 it=qi 的条件下，从 t+1 到 T 的部分观测序列为 ot+1,ot+2,⋯,oT 的概率为后向概率：

βt(i)=P(ot+1,ot+2,⋯,oT|it=qi,λ)

观测序列概率的后向算法：
输入：HMM λ=(A,B,π) ，观测序列 O
输出：观测序列概率 P(O|λ)
（1）规定初始后向概率

βT(i)=1

（2）向前递推

βt(i)=P(ot+1,ot+2,⋯,oT|it=qi,λ)=∑j=1Naijbj(ot+1)P(ot+2,ot+3,⋯,oT|it+1=qj,λ)=∑j=1Naijbj(ot+1)βt+1(j)

（3）整体观测序列

P(O|λ)=P(o1,o2,⋯,oT|λ)=P(o1)P(o2,o3,⋯,oT|λ)=∑i=1NP(i1=qi)P(o1|i1=qi)P(o2,o3,⋯,oT|i1=qi,λ)=∑i=1Nπibi(o1)β1(i)

最后，在给定HMM λ=(A,B,π) 和观测序列 O 的条件下，可利用前向概率和后验概率计算单个状态和两个相邻状态：
（1）时刻 t 处于状态 qi ：

γi(t)=P(it=qi|O,λ)=P(it=qi,O|λ)P(O|λ)=P(it=qi,O|λ)∑j=1NP(it=qj,O|λ)=αt(i)βt(i)∑j=1Nαt(j)βt(j)=∑j=1Nαt(i)aijbj(ot+1)βt+1(j)∑i=1N∑j=1Nαt(i)aijbj(ot+1)βt+1(j)

（2）时刻 t 处于状态 qi ，时刻 t+1 处于状态 qj ：

ξt(i,j)=P(it=qi,it+1=qj|O,λ)=P(it=qi,it+1=qj,O|λ)P(O|λ)=P(it=qi,it+1=qj,O|λ)∑i=1N∑j=1NP(it=qi,it+1=qj,O|λ)=αt(i)aijbj(ot+1)βt+1(j)∑i=1N∑j=1Nαt(i)aijbj(ot+1)βt+1(j)

HMM生成，参数学习算法

（1）给定观测序列的同时，也给定了状态序列，用极大似然估计得 λ=(A,B,π) 。有关MLE的内容参考http://blog.csdn.net/cymy001/article/details/78016109

若训练数据含 S 个等长的观测序列和对应的状态序列 {(O1,I1),(O2,I2),⋯,(OS,IS)} ，则记 S 个序列的每个状态序列中，任何起始时刻，只要该起始时刻处于状态 i ，并且它的下一时刻处于状态 j ，则计入频数统计量 Aij ，那么可得 aij 的MLE

aij=Aij∑j=1NAij

同样， S 个序列的每个状态序列中，任何起始时刻，只要状态序列在该时刻处于状态 j ，观测序列在该时刻处于观测 k ，则计入频数统计量 Bjk ，可得 bj(k) 的MLE

bj(k)=Bjk∑k=1MBjk

对于初始状态概率，只需要统计状态序列集合 {O1,O2,⋯,OS} 中每个序列的第一个元素状态频数，再除以 S ，即得各个初始状态概率的MLE。

（2）只给观测序列，可以把状态序列看成隐变量，用EM算法得 λ=(A,B,π) 。有关EM算法的内容参考http://blog.csdn.net/cymy001/article/details/78264648
目标是使含隐变量（这里是“状态变量”）的观测序列概率随着参数 λ 的迭代计算，逐步增大，而这个问题可以通过降低下界的办法转化成EM算法的 Q 函数极大化问题，即

Q~(λ,λ¯)=EI[logP(O,I|λ)|O,λ¯]=∑IlogP(O,I|λ)P(I|O,λ¯)=∑IlogP(O,I|λ)P(O,I|λ¯)P(O|λ¯)∝∑IlogP(O,I|λ)P(O,I|λ¯)=Q(λ,λ¯)

给定待优化的变量记号：初始状态概率 πi1 ，状态转移概率 aitit+1 ，观测概率 bit(ot) ，则

P(O,I|λ)=πi1bi1(o1)ai1i2bi2(o2)⋯aiT−1iTbiT(oT)

于是

Q(λ,λ¯)=∑IlogP(O,I|λ)P(O,I|λ¯)=∑Ilogπi1P(O,I|λ¯)+∑I(∑t=1T−1logaitit+1)P(O,I|λ¯)+∑I(∑t=1Tlogbit(ot))P(O,I|λ¯)=∑i=1NlogπiP(O,i1=i|λ¯)+∑i=1N∑j=1N(∑t=1T−1logaij)P(O,it=i,it+1=j|λ¯)+∑j=1N(∑t=1Tlogbj(ot))P(O,it=j|λ¯)

分别对上式和的三个部分利用 Lagrange 乘子法求解，即

L(πi)=∑i=1NlogπiP(O,i1=i|λ¯)+θ1(∑i=1Nπi−1)L(aij)=∑i=1N∑j=1N(∑t=1T−1logaij)P(O,it=i,it+1=j|λ¯)+θ2(∑j=1Naij−1)

L(bj(k))=∑j=1N(∑t=1Tlogbj(ot))P(O,it=j|λ¯)+θ3(∑k=1Mbj(k)−1)

分别对 πi,aij,bj(k) 求导进行相关计算，即可得HMM的参数

πi=P(O,i1=i|λ¯)P(O|λ¯)=γ1(i)aij=∑t=1T−1P(O,it=i,it+1=j|λ¯)∑t=1T−1P(O,it=i|λ¯)=∑t=1T−1ξt(i,j)∑t=1T−1γt(i)bj(k)=∑t=1TP(O,it=j|λ¯)I(ot=vk)∑t=1TP(O,it=j|λ¯)=∑t=1,ot=vkTγt(j)∑t=1Tγt(j)

Baum_Welch算法：
输入：观测序列 O
输出：HMM的参数 λ=(A,B,π)
（1）初始模型参数 λ(0)=(A(0),B(0),π(0))
（2）利用上述推导公式迭代计算

a(n+1)ij=∑t=1T−1ξt(i,j)∑t=1T−1γt(i)，bj(k)(n+1)=∑t=1,ot=vkTγt(j)∑t=1Tγt(j)，π(n+1)i=γ1(i)

（3）满足终止条件时，输出模型参数 λ(n+1)=(A(n+1),B(n+1),π(n=1))

HMM状态序列预测算法

给定HMM和观测序列，预测该观测序列对应的状态序列，也就是其对应的标签序列。
（1）贪婪的近似算法：即每一时间步都选取“当前时刻对应的状态概率最大的状态点”，这种办法会产生实际状态转移矩阵 A 中相邻转移概率为 0 的矛盾相邻转移状态。

（2）维特比算法：利用动态规划的思想，将寻找最优状态路径的问题递归成最优子状态路径问题，求解的过程是从前向后按层递推求解最大概率路径。
有关动态规划请参考http://blog.csdn.net/cymy001/article/details/78474263

定义在时刻 t 状态为 i 的所有前半段的单个路径 (i1,i2,⋯,it) 中概率最大值为

δt(i)=maxi1,i2,⋯,it−1P(it=i,it−1,⋯,i1,ot,⋯,o1|λ)，i=1,2,⋯,N

有如下递推关系

δt+1(i)=maxi1,i2,⋯,itP(it+1=i,it,⋯,i1,ot+1,⋯,o1|λ)=max1≤j≤N[δt(j)aji]bi(ot+1)，i=1,2,⋯,N

定义在时刻 t 状态为 i 的所有前半段的单个路径 (i1,i2,⋯,it−1,i) 中概率最大的路径对应的第 t−1 个结点为

ψt(i)=argmax1≤j≤N[δt−1(j)aji]，i=1,2,⋯,N

维特比算法：
输入：HMM参数 λ=(A,B,π) ，观测序列 O
输出：最优状态序列 I∗
（1）初始化

δ1(i)=πibi(o1),ψ1(i)=0，i=1,2,⋯,N

（2）向后递推计算 t=2,3,⋯,T

δt(i)=max1≤j≤N[δt−1(j)aji]bi(ot)，ψt(i)=argmax1≤j≤N[δt−1(j)aji]，i=1,2,⋯,N

（3）终止

P∗=max1≤i≤NδT(i)，i∗T=argmax1≤i≤N[δT(i)]

（4）最优路径回溯
对 t=T−1,T−2,⋯,1 ，求

i∗t=ψt+1(i∗t+1)

即可得最优路径 I∗ 。
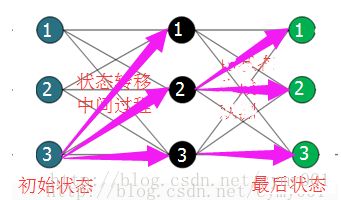
求解最优路径的过程，就是一个对状态转移中按层形成的完全有向图状态转移网络进行最大化过滤的过程。

如上图所示，这一个将状态变化过程展开的网络图，在前面前向概率和后向概率计算时，是对相邻层之间的状态点进行了遍历（即上图细线，第一层状态123分别会与第二层状态123连接映射），但是维比特算法中，只会追踪映射出来的对应本层概率最大的前一层点，比如绿色层状态1，可以由黑色层123三个点分别映射出对应路径，但是黑色层状态2映射到绿色层状态1的路径观测概率最大，所以只考虑这条路径。