【深度学习入门】mnist手写数字识别
目录
- 数据预处理
- 相关原理
- 卷积
- 池化
- 过拟合现象
- 全连接层
- logits、loss、accuracy
- 搭建模型
- 训练&可视化
- 自己制作测试集
- Problems
mnist是深度学习的“hello world”,谷歌、tensorflow官网都有详尽的教程介绍如何上手。之前的项目大多是在别人写好的框架上修改、发挥,理论上对原理算是熟悉的了,但是许多函数的理解有点知其然不知其所以然。因此想借这个项目,完全手动写一个CNN模型,好好地熟悉一下tensorflow框架。果然在写的过程中,踩到了许多雷。
tensorflow用的还是1.14.0版本,在使用过程中感觉许多函数功能相近,非常累赘,2.0有更加精简的框架。由于担心兼容性问题,暂时还是使用旧版本。
数据预处理
MNIST 数据集包含四个部分:
Training set images: train-images-idx3-ubyte.gz (9.9 MB, 解压后 47 MB, 包含 60,000 个样本)
Training set labels: train-labels-idx1-ubyte.gz (29 KB, 解压后 60 KB, 包含 60,000 个标签)
Test set images: t10k-images-idx3-ubyte.gz (1.6 MB, 解压后 7.8 MB, 包含 10,000 个样本)
Test set labels: t10k-labels-idx1-ubyte.gz (5KB, 解压后 10 KB, 包含 10,000 个标签)
作为tensorflow的入门级数据集,在tensorflow中已经内载了方便使用和下载的api,可以通过简单的代码下载并查看数据集内容。
def dataset_intro(args):
data_dir = args.data_dir
# read_data_sets 会自动判断当前目录下数据集是否已经存在
mnist = input_data.read_data_sets(data_dir, one_hot=True)
# 查看是否下载成功
# 784=28*28 10=10*1
print(mnist.train.images.shape, mnist.train.labels.shape) # (55000, 784) (55000, 10)
# 查看测试集数据大小
print(mnist.train.images.shape, mnist.train.labels.shape) # (10000, 784) (10000, 10)
# 打印出第0幅图片的向量表示
print(mnist.train.images[0, :])
# 打印出第0幅图片的标签
print(mnist.train.labels[0, :])
one_hot_label = np.argmax(mnist.train.labels[0, :])
print(one_hot_label)
# 使用jpg形式查看图片
save_dir = 'MNIST_data/draw/'
if os.path.exists(save_dir) is False:
os.makedirs(save_dir)
# 保存前20张图片为png形式
for i in range(20):
image_array = mnist.train.images[i, :]
image_array = image_array.reshape(28, 28)
image_array = image_array*255
filename = save_dir + 'mnist_train_%d.png' % i
img = Image.fromarray(image_array)
if img.mode == "F":
img = img.convert('RGB')
img.save(filename)
x = imgplt.imread('MNIST_data/draw/mnist_train_0.png')
plt.imshow(x)
plt.show()
每张图片是大小为28×28的二值图像,以[784×1]的数组形式存储,其label使用one-hot形式存储。可以从下面的图片中很直观地理解存储方式。

在处理过程中,有两点需要注意一下:
- 在矩阵中,存储的数值处于[0, 1]之间,如果直接用
matplotlib包的Image.fromarray(),save后会出现图片纯黑的情况。这是因为,png是以[0, 255]表示灰度值,需要image_array = image_array*255将矩阵扩展。 - 使用PIL模块存储图像时,遇到了存储失败的问题:
OSError: cannot write mode F as JPEG
这是因为PIL有八种不同的颜色模块,其中灰度图像对应了F I L三种格式:
模式
1 1位像素,黑和白,存成8位的像素
L 8位像素,黑白
P 8位像素,使用调色板映射到任何其他模式
RGB 3×8位像素,真彩
RGBA 4×8位像素,真彩+透明通道
CMYK 4×8位像素,颜色隔离
YCbCr 3×8位像素,彩色视频格式
I 32位整型像素
F 32位浮点型像素
只需要将图片模式转为RGB就能顺利运行。
除此之外,无需其他特殊处理。
相关原理
卷积
卷积的概念是从猫的感受野引申过来的。在猫的视觉感受皮层中,每个神经元只和上一层的神经元相连接。可以用手电筒照墙壁来理解卷积的概念,手电筒在墙壁上探照的区域,就是感受野。手电筒接收了这一块区域的信息,就是卷积对这一块操作所提取的特征。层层卷积下去,最后只需要一个点,就能概括所有的信息。因此卷积是从将低维特征映射到高维特征的操作。
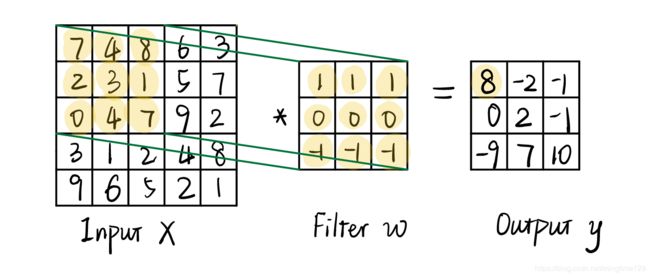
如上图所示,输入X可以看做一个5×5的灰度图像,filter大小为3×3,即卷积核,在步长为(1×1)的情况下,最终输出得到大小为3×3。卷积运算就是用卷积核覆盖在图像上,与覆盖区域进行乘加运算,例如图中黄色区域的卷积计算为:
7 ∗ 1 + 4 ∗ 1 + 8 ∗ 1 + 2 ∗ 0 + 3 ∗ 0 + 1 ∗ 0 + 0 ∗ ( − 1 ) + 4 ∗ ( − 1 ) + 7 ∗ ( − 1 ) = 8 7*1+4*1+8*1+2*0+3*0+1*0+0*(-1)+4*(-1)+7*(-1)=8 7∗1+4∗1+8∗1+2∗0+3∗0+1∗0+0∗(−1)+4∗(−1)+7∗(−1)=8
值得一提的是,上图演示的filter是图像处理中用于水平边缘检测的prewitt算子,能有效弱化中间部分。 w w w是神经网络需要学习的参数,不断优化网络提取特征的能力。
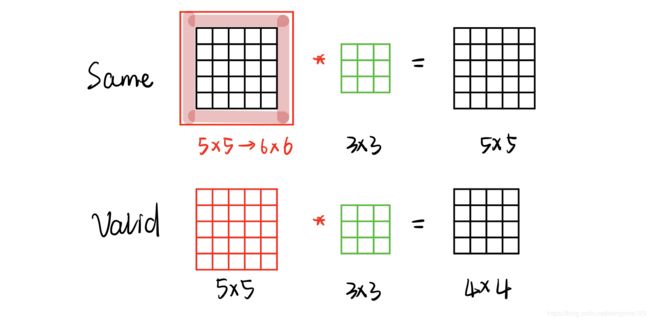
t e n s o r f l o w tensorflow tensorflow框架中提供了两种padding模式: s a m e same same 和 v a l i d valid valid
v a l i d valid valid就是不对图像进行额外的操作,对于大小为 m ∗ m m*m m∗m的图像,使用 n ∗ n n*n n∗n的卷积核,当步长为(1×1)时,得到的输出为 ( m − n + 1 ) ∗ ( m − n + 1 ) (m-n+1)*(m-n+1) (m−n+1)∗(m−n+1)。使用这种卷积方式,图像边缘信息只有一次参与计算的机会,可能会浪费掉大量的特征信息。
s a m e same same解决了上述问题,如图所示,函数在进行卷积操作之前,会先扩充矩阵,使得 ( m + k ) % n = = 0 (m+k)\%n==0 (m+k)%n==0,使用这种方式卷积后的输出大小与输入一致。*
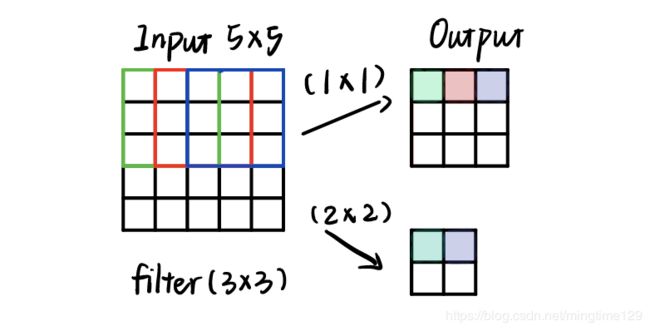
步长是另一项与特征信息提取有关的重要参数。在上述的例子中,步长均为1,即卷积核每次移动一个单元对图像进行卷积操作。如果步长加大,如上图的(2*2),在其他条件不变的情况下,输出显著减少,这意味着计算得到了精简,同时提取的信息也减少了,在底层的卷积中,这并不是好事,意味着可能过早地丢失了底层信息。
综上所述,我们可以得到,对于步长为S,填充为p,得到的卷积输出为:
( m − n + 2 ∗ p ) / S + 1 (m-n+2*p)/S+1 (m−n+2∗p)/S+1
池化
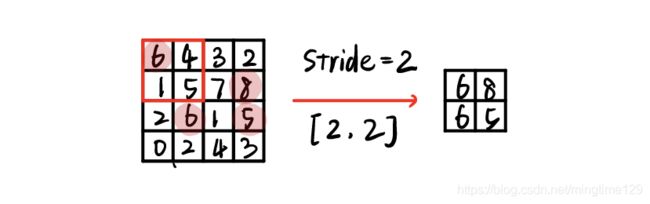
常用的池化方式有平均池化(meaning_pool)、最大池化(max_pooling)等。在卷积和池化层中间通常会有一个线性整流层(Relu)激活卷积后的特征图。池化得到的结果可以理解为对特征图的进一步筛选。如上图所示,采用的最大池化,步长为(2*2),提取每个区域的最大值。池化的作用是:
- 提取某一个区域内最具有代表性的特征。
- 进一步减少卷积后的数据量,弱化计算。
- 弱化卷积特征与原图像的匹配程度,避免过拟合现象。
过拟合现象
所谓过拟合,顾名思义,就是模型对训练集的拟合效果过好,导致模型在测试集上正确率会很低。常见的原因包括:
- 建模样本噪音过大。测试集和训练集差异较大,学习了训练集中的噪声和不具有代表性的特征,网络对测试集的分辨能力较低。
- 训练的样本过少,模型学习得不够充分。
- 样本类别不均衡,模型像某一种类别倾斜。
- 模型太过复杂,参数过多,完美拟合训练集。
针对上述问题,解决方法如下:
- 限制训练时间,避免模型对训练集过于完美地拟合。
- 适当降低模型复杂度或获取大量的样本数据,使模型学习更多的样本和“特例”。
- 使用不同的预处理方法清洗样本,滤除杂音,保留标志性特征。
- 对类别间数量差异过大的样本进行过采样或欠采样,平衡模型预测能力。
- 限制权值,使用L2正则化函数。在梯度下降的过程中,神经网络不断朝cost趋于0的方向训练,如果在损失函数cost后加入一项永不为0的项,那么cost永远大于0,无法完美契合训练集,限制了过拟合的现象。
- 在隐藏层后添加dropout层,这是一个简单又高效的方法。在训练中,如图14所示,正向传播时全连接层随机忽略某些节点,这使得每一次训练,隐层传递出来的信息都是与上一次不同的,是一个“新”的网络。反向传播时,没有被“删除”的结点得到更新,被隐藏的结点保留之前的参数。
全连接层
在卷积部分结束后,通常会接一个全连接层,承担分类工作。全连接层入门详解←一篇写得非常通俗易懂的文章。总而言之,全连接层的作用是弱化特征位置对分类结果的影响。在实际使用时,经过卷积层出来的数据,我们需要先进行flatten,如图像大小为 7 ∗ 7 7*7 7∗7,flatten后展开为 1 ∗ 49 1*49 1∗49,那么要如何将所有特征高度浓缩整合为一个值呢?用矩阵 49 ∗ 1 49*1 49∗1便可以轻易办到。如果全连接层有 1024 1024 1024个神经元,那么 49 ∗ 1024 49*1024 49∗1024便可以得到 1 ∗ 1024 1*1024 1∗1024的全连接层输出。
大多数时候全连接层不只一层,是为了提高模型的非线性表达能力。最后一层全连接层的神经元数为分类数目,初步得到模型计算的在该类别上的数值。
logits、loss、accuracy
从全连接层输出的shape为[1*10]的logits是模型判断的、该样本在各类别上的特征值,或者说,该样本含有多少的某一类特征。
s o f t m a x softmax softmax则计算出输入为x,样本为类别 j j j的概率是 P ( y = j ∣ x ) P(y=j|x) P(y=j∣x)。
P ( y = j ∣ x ) = e x j ∑ k = 1 K e x j P(y=j|x)=\dfrac{e^{x_j}}{\sum_{k=1}^K e^{x_j}} P(y=j∣x)=∑k=1Kexjexj
以手写数字8为例,字体如图:
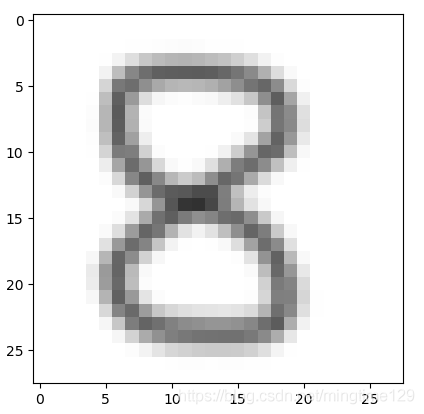
全连接层得到该图片的特征值为:
[-6.17017 -4.24155 1.6469325 5.7293806 -6.5731936
0.28266746 -1.5470302 -4.6259646 10.159533 -0.36437735]
由此可以得到 e x j e^{x_j} exj:
[0.00209088087538757, 0.014385277823915611, 5.191031799511044, 307.7785736182166,
0.0013973278425530296, 1.3266639170588774, 0.2128792425355013, 0.0097942025824738,
25836.21701929931, 0.6946290272855455]
得到该图片在每一类别上的可能性:可以看到,有98.8%的概率为数字8,经过argment函数后,得到8,为网络的预测输出。
[[0.00000008 0.00000055 0.0001985 0.01176908 0.00000005
0.00005073 0.00000814 0.00000037 0.9879459 0.00002656]]
该模型使用交叉熵损失函数,tensorflow函数为 t f . n n . s p a r s e _ s o f t m a x _ c r o s s _ e n t r o p y _ w i t h _ l o g i t s ( ) tf.nn.sparse\_softmax\_cross\_entropy\_with\_logits() tf.nn.sparse_softmax_cross_entropy_with_logits(),第一步的工作就是 s o f t m a x softmax softmax,上面已经做过了,仅需考虑 c r o s s _ e n t r o p y cross\_entropy cross_entropy:
H y ′ = − ∑ i y i ′ l o g ( y i ) H_{y'}=-\sum_{i} {y_i}'log{(y_i)} Hy′=−i∑yi′log(yi)
其中 y i ′ {yi}' yi′为one-hot格式的label中的第 i i i个值, y i {yi} yi为经softmax归一化输出的vector中的对应分量,当分类越准确时,所对应的分量就会越接近于1,从而值也就会越小。
同样以上图得到的输出为例,
y'=[[0.00000008 0.00000055 0.0001985 0.01176908 0.00000005
0.00005073 0.00000814 0.00000037 0.9879459 0.00002656]]
y =[0, 0, 0, 0, 0, 0, 0, 0, 1, 0]
l o s s = − ( 0 ) ∗ l o g ( 0.00000008 ) + . . . + 1 ∗ l o g ( 0.9879459 ) + . . . = 0.012127356 loss = -{(0)* log(0.00000008)+...+1*log(0.9879459)+...}=0.012127356 loss=−(0)∗log(0.00000008)+...+1∗log(0.9879459)+...=0.012127356
自适应优化器的目标就是通过不断的训练使loss的值减小。
搭建模型
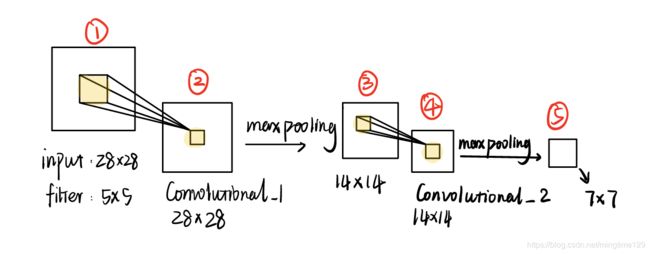
输入是55000张存储形式为[1 * 784]的灰度图片,,reshape为[28 * 28]后作为网络的输入。构建双层卷积层。每层参数的输入输出如表格所示:
| parameters | Output | |
|---|---|---|
| 输入层 | batchsize * 28 * 28 * 1 | |
| conv2d_1 | Kernelsize=[5, 5], num=32,padding=same,strides =[1, 1] | batchsize * 28 * 28 * 32 |
| max_pooling2d_1 | Kernelsize=[2, 2], strides = [2, 2] | batchsize * 14 * 14 * 32 |
| conv2d_2 | Kernelsize=[5, 5], num=64,padding=same,strides =[1, 1] | batchsize * 14 * 14 * 64 |
| max_pooling2d_2 | Kernelsize=[2, 2], strides = [2, 2] | batchsize * 7 * 7 * 64 |
| fc_1 | reshape为[batchsize , 7 * 7 * 64],units = 1024 | batchsize * 1024 |
| fc_2 | units = 10 | batchsize * 10 |
该部分代码如下:
with tf.name_scope('input_layer'):
x = tf.placeholder("float", shape=[None, 784]) # 28*28=784
y = tf.placeholder("float", shape=[None, 10]) # 10个类别
keep_prob = tf.placeholder(tf.float32, name='keep_prob')
# -1表示一个batch的图片数 1表示灰度图片只有一个通道
input_x = tf.reshape(x, [-1, 28, 28, 1])
with tf.name_scope('conv2d_1'):
conv2d_1 = tf.layers.conv2d(inputs=input_x,
filters=32,
kernel_size=[5, 5],
strides=[1, 1],
activation=tf.nn.relu,
use_bias=True,
padding='same')
shape = conv2d_1.get_shape().as_list()
print(shape)
with tf.name_scope('max_pooling1d_1'):
max_pooling2d_1 = tf.layers.max_pooling2d(inputs=conv2d_1,
pool_size=[2, 2],
strides=[2, 2],
padding='same')
shape = max_pooling2d_1.get_shape().as_list()
print(shape)
with tf.name_scope('conv2d_2'):
conv2d_2 = tf.layers.conv2d(inputs=max_pooling2d_1,
filters=64,
kernel_size=[5, 5],
strides=[1, 1],
activation=tf.nn.relu,
use_bias=True,
padding='same')
shape = conv2d_2.get_shape().as_list()
print(shape)
with tf.name_scope('max_pooling1d_2'):
max_pooling2d_2 = tf.layers.max_pooling2d(inputs=conv2d_2,
pool_size=[2, 2],
strides=[2, 2],
padding='same')
# max_pool_1 = (batch_size*n_channels, 5, 32)
shape = max_pooling2d_2.get_shape().as_list()
print(shape)
with tf.name_scope('fc_layer'):
# 进入全连接层前,需要将feature展开成一维
fc_para = shape[1]*shape[2]*shape[3]
print("fc_layer")
print(fc_para)
pool_flat = tf.reshape(max_pooling2d_2, [-1, fc_para])
fc = tf.layers.dense(inputs=pool_flat,
units=1024,
activation=tf.nn.relu,
use_bias=True,
name='fc1'
)
fc_dropout = tf.layers.dropout(fc, keep_prob)
fc_output = tf.layers.dense(inputs=fc_dropout,
units=num_classes,
use_bias=True,
name='fc2'
)
训练&可视化
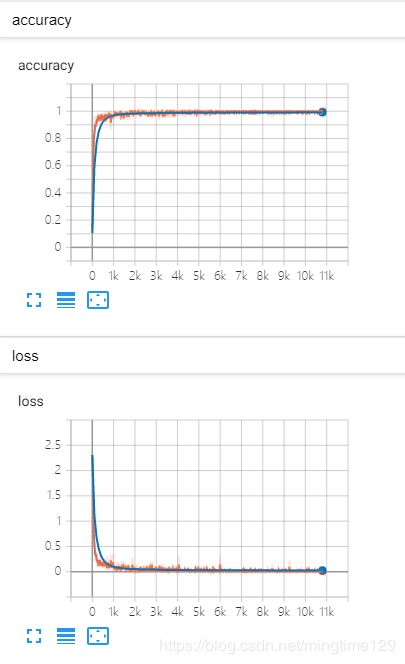
学习率为1e-4,batchsize大小为64,训练10000步后,保存在测试集上全局准确率最高的模型。准确率最高为99.3%。同时使用tensorboard可视化训练过程。
step 9910, training accuracy 1.000, loss 0.008
step 9920, training accuracy 1.000, loss 0.002
step 9930, training accuracy 1.000, loss 0.006
step 9940, training accuracy 1.000, loss 0.001
step 9950, training accuracy 1.000, loss 0.003
step 9960, training accuracy 1.000, loss 0.006
step 9970, training accuracy 1.000, loss 0.003
step 9980, training accuracy 1.000, loss 0.002
step 9990, training accuracy 1.000, loss 0.006
step 10000, training accuracy 1.000, loss 0.009
-------- testing accuracy 0.993, loss 0.029
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 978 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1131 | 2 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 1027 | 1 | 0 | 0 | 0 | 3 | 0 | 0 |
| 3 | 0 | 0 | 2 | 1006 | 0 | 2 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 975 | 0 | 0 | 0 | 0 | 6 |
| 5 | 1 | 0 | 0 | 7 | 0 | 882 | 1 | 0 | 0 | 1 |
| 7 | 3 | 2 | 0 | 1 | 2 | 2 | 948 | 0 | 0 | 0 |
| 7 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 1019 | 1 | 4 |
| 8 | 2 | 0 | 1 | 2 | 0 | 1 | 0 | 2 | 961 | 5 |
| 9 | 0 | 0 | 0 | 0 | 2 | 3 | 0 | 1 | 0 | 1003 |
自己制作测试集
测试只需要调用保存的模型,传入图片就可以了,过程很简单:
- 读取图片,并将其转化为矩阵存储形式:
img_files = os.listdir(dir)
img_set = []
for file in img_files:
file = os.path.join(dir, file)
img = Image.open(file)
img = img.convert('F')
img_data = list(img.getdata())
img_norm = [(255-x)*1.0/255.0 for x in img_data]
img_set.append(img_norm)
- 调用模型
placeholders, metrics, train_op = cnn.create_model(10, 1e-4)
figure, label, keep_prob = placeholders
logits, loss, accuracy, y_pred, y_true = metrics
checkpoint_dir = 'cnn2/'
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
ckpt = tf.train.get_checkpoint_state(checkpoint_dir)
saver.restore(sess, tf.train.latest_checkpoint(checkpoint_dir))
output = y_pred.eval(feed_dict={figure: test_img, keep_prob: 1.0}, session=sess)
print(output)
为了方便,这里使用的是ps直接制作,用了家人和自己手写的字迹进行测试,需要注意的是每张图片大小都必须为28*28,除了数字6识别失败,其他数字的识别结果都很好。

Problems
-
可能的数据泄露
由于没有在官网找到更详细的信息,所以猜测同一个人可能书写了多遍同一个数字,并且这些样本可能会均匀地散布在训练集和测试集中。因此模型在测试集上能达到非常好的训练效果。
但是考虑到数字的信息量简单,并且在自己制作的样本集上也取得了非常好的效果,因此可能影响不是很大。 -
数字6识别失败

上图中有两个6识别错误,可以猜想是哪两个?是最端正的两个手写体,即后两个。其实原因很简单,因为训练数据来自西方人的手写体,和中方存在差异。因此写的越歪,识别越准确orz。
如果数据集中加入中方手写体,那么就能对中式6较好地辨认。


-
数据增强
不管一幅图像如何颠倒旋转,扭曲变形,人眼总能迅速判断出原图。而机器不行,机器对位置、形态的变化非常敏感。以下图为例,所有数字向右旋转45度,识别准确率由6/7下降至3/7。

如果大幅度缩小数字在图片中的位置呢?或者加上噪声、模糊?对于可能预见到的干扰模型测试准确率的情况,解决的方法就是增强数据:采用模糊、噪声、旋转等方式就能制造出更多形态的样本。
更多数据增强相关 -
自适应优化器
-
可能遇见的坑
5.1 数据集是以【0,1】形式存储的,而PIL包中的灰度级别分布是从【0,255】,因此若是需要显示or保存图片,需要先将矩阵*255,同样,若是要使用模型
处理图片,则需要将矩阵归一化。
5.2 使用tf.nn.sparse_softmax_cross_entropy_with_logits函数计算loss时,有两个参数logits和labels,其中logits是全连接层的输出,shape为[batchsize, num_classes],而labels是图片的标签,必须为非one-hot形式。
5.3 如果由于特殊需要,写入tensorboard的参数是用numpy计算的,也就是说非直接的tensor,那么可以通过如下方式打包参数:test_summary_str = tf.Summary(value=[ tf.Summary.Value(tag="loss", simple_value=test_loss), tf.Summary.Value(tag="accuracy", simple_value=test_accuracy), ])5.4
tf.nn.conv2d与tf.layers.conv2d没有太大的区别,后者使用更加便捷,且参数自动初始化,前者需要手动初始化变量。