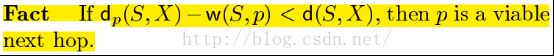多路径路由算法简单总结：LFI、MDVA、MPA、MPDA、MPATH

最近看了一些论文，多路径路由算法的。比较晦涩，还是勉强总结了一点内容：

Multi-path routing algorithms总结

Problem formulation 2

MPA(Multiple Path Algorithm) 2

MPA算法解决的问题 2

MPA使用的本质思想 3

MPA执行过程 3

MDVA(Distance-Vector Multipath) 4

MDVA算法解决的问题 4

MDVA使用的本质思想 5

MDVA执行过程 6

MPDA(Multipath Partial Dissemination Algorithm) 6

MPDA使用的本质思想 6

MPDA可以借鉴的地方 7

MPATH Routing Algorithm 7

MPATH使用的本质思想 7

MPATH可以借鉴的地方 8

这些Multi-Path的共同点 8

在SPA基础上保证无环LFI 8

在保证无环的时候引用了关键的SINK点状态变量 9

 

Problem formulation

 

——摘自MDVA

【problem formulation】

对每一个源点i，要找到S(i, j) belongs to N(i)，使i可以经过S(i, j)中的点到达对应的终点j。如果对每个终点j，能找到SG(j)，就可以解决问题。

 

MPA(Multiple Path Algorithm)

MPA算法解决的问题

1）可以找到多条路径，而不是全部路径，使用“可行下一跳”这个词汇；

2）构造了高效的数据结构，运算快；

3）next hop有权重，易于QoS；

4）直接用于实际网络，可以和OSPF混合使用。

 

MPA使用的本质思想

 

 

MPA执行过程

MPA本质，对任意一个源点路由器i，都要记录三个信息：

i到目标点路由器j的距离：D(i, j)；i经过每一个邻居路由器k到达j的距离：Dk(i, j)【上面两个距离使用任意的SPA都可以计算得到】；i到每一个邻居路由器k的距离：l(i, k)

那么：只要满足Dk(i, j) - l(i, k) < D(i, j)，则k即为可行下一跳。

 

注意，本篇论文并没有给出伪代码；MPA能够找到的viable next hop的数量取决于使用的underlying SPT algorithm。

 

MDVA(Distance-Vector Multipath)

MDVA算法解决的问题

1）解决 分布式贝尔曼福德算法求最小路径的“计数到无穷问题”（本身是由于“有环”（只交换距离信息而不交换路径信息）造成的！）

2）同时可以找到multi-paths，【有环】或者【计数到无穷】这样的问题可以通过寻找SG(j)这样的DAG来解决！

 

 

MDVA使用的本质思想

对于源点i的任意邻居节点k，只有邻居节点k到目标节点j的距离 小于 源点i到目标节点j的距离，这样的邻居才是MDVA考虑的。如下所述：

 

同时保证无环：

 

 

MDVA执行过程

如下所述（详细过程参考原文献），注意，distances信息只通过SGj传递（本质上可以防止loop的发生）！

 

MDVA算法的细节，主要是找S(i, j)：

实现时，【直接维护】loop-free invariant conditions中提到的D(k, ji)，FD(i, j)，S(i, j)，D(i, jk)等变量，进而找到S(i, j)。

与MPA算法的思想一致，区别在于，MPA维护三类信息（D(i, j)，D(k, j)，l(i, k)），直接使用D(i, j) - l(i, k) < D(k, j)来构造S(i, j)，更直接，更易理解！

伪代码参考原文献。

 

MPDA(Multipath Partial Dissemination Algorithm)

MPDA使用的本质思想

先构建一个SPA算法，再在基础算法上添加LFI限制即可：

 

 

MPDA算法的伪代码。相对于PDA而言，使用了active和passive两种状态来标记一个路由器是否处于【等待邻居路由器确认】的状态，只有处于passive状态（所有邻居路由器对他发出去的LSU message都给出了确认）时，才会进一步计算main topology table。

整个思路和PDA一样。当每个路由器接到一个event【接收到一个LSU或者检测到邻居的down】之后，做以下操作：

1）计算neighbor topology table，T(i, k)；

2）【【【等到该路由器处于passive状态（所有邻居路由器对他发出去的LSU message都给出了确认）时】】】，才计算main topology table，T(i)；通过merge T(i, k)和l(i, k)计算T(i)。

3）如果T(i)的某些entry变化，则根据变化发送特定【add/del/change】的LSU message给所有邻居。

4）所有路由器repeated执行上面的操作直到系统稳定。

 

 

MPDA可以借鉴的地方

“2.3.2 Correctness Proof of PDA”部分，证明一个最短路径算法的正确性。

“2.3.4 Correctness Proof of MPDA”部分，证明一个Multi-path算法的正确性。

 

MPATH Routing Algorithm

MPATH使用的本质思想

从终点的角度考虑问题（而不是从起点），并且利用终点的前一个节点做路由计算。也是先构建一个PATH算法，再在基础算法上添加LFI限制（整个思路和MPDA完全一样，仅仅是the type of messages exchanged不同而已！另外还包含了一个predecessor node，所以要处理该node相关的距离更新）。

 

 

 

MPATH可以借鉴的地方

“2.4.2 Correctness Proof of MPATH”部分，证明一个Multi-path算法的正确性。

 

这些Multi-Path的共同点

在SPA基础上保证无环LFI

主要是保证无环，多路径才能有效。两种表达无环的方法（用于指导算法设计、证明算法正确性）：

方式一：

方式二：

 

在保证无环的时候引用了关键的SINK点状态变量

不管使用哪种算法，除了维护保证LFI的基本信息外，都还维护了某次距离更新是否结束的标志（有使用passive/active对，也有使用query/reply对，同时联想到第二部分中有使用cycle number来标记某轮迭代）。如果一轮迭代没有结束（对于发出update message的节点 i ，结束的标志是 i 收到了所有他的邻居对该message的回复），那么新的update不能开始，这种方式保证在一轮迭代的时间内LFI。或者更直接的，不管该轮迭代结不结束，直接发出更大的cycle number迭代也可以。【貌似我们的设计也逃脱不了这种规律】

简单总结：

1）两种形式的问题表述（LFI）

2）MDVA：直接维护LFI中提到的FD(i, j) D(i, jk) FD(i, j)这三个信息，是一种距离矢量算法

3）MPA：直接维护Dk(i, j) - L(i, k) < D(i, j)这三个信息，原文中未给出伪代码，是一种链路状态算法

4）MPDA：直接维护LFI中提到的FD(i, j) D(i, jk) FD(i, j)这三个信息，是一种链路状态算法

5）MPATH：使用了predecessor node，即终点的前一个node，而不是使用源点的下一个node k，但本质应该没变

MDVA和MPDA的本质没区别，只是首先细节不一样。两个算法中，FD(i, j)的计算需要通过设置passive和active两个状态来表明本路由器是否处于“稳定状态”（是否在等待邻居回应自己发出的update message）。

注意，FD(i, j)之所以可以计算，是因为FD(i, j)虽然是Dk(j, i)的延迟版本，但只要在等待回应的时间内（active状态时）满足LFI，就能保证无环，计算出来的FD(i, j)就会保证有效。——该定理在论文中有证明，此处省略。