斯坦福大学深度学习公开课cs231n学习笔记（5）神经网络结构与激活函数

在线性分类器中，使用公式：对图像进行分类，神经网络则使用另外一种公式：,这里只是两层的网络结构，参数W1和W2在反向传播过程中，通过链式法则得到。

神经网络与大脑神经结构

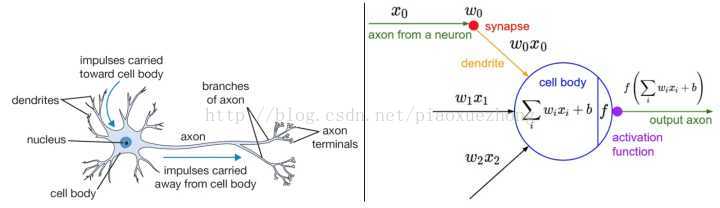
上图1中，左边是人脑的神经元结构，右边是神经网络数学模型。

其中，生物神经元：从树突（dendrites）获取输入信号，然后沿着它唯一的轴突（axon）产生输出信号；轴突在其末端逐渐分枝，通过突触（synapses）和其他神经元的树突相连。

神经网络模型：信号 x0 沿着轴突传播，将基于突触的强度（如w0），与其他神经元的树突进行交互（比如w0x0）。其中，突触的强度（即权重w）是可以学习的，并且控制着一个神经元对另一神经元的影响强度和影响方向（正权重使其兴奋，负权重使其抑制）。在图1右边的基本模型中，多个信号在细胞体（cell body）中相加，如果累加和大于某个阈值，那么使得该神经元被激活，轴突输出一个峰值信号。

class Neuron(object):
  # ... 
  def forward(self, inputs):
    """ assume inputs and weights are 1-D numpy arrays and bias is a number """
    cell_body_sum = np.sum(inputs * self.weights) + self.bias
    firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # sigmoid activation function
    return firing_rate

常用的激活函数：

（1）sigmoid函数：
（2）tanh函数：     

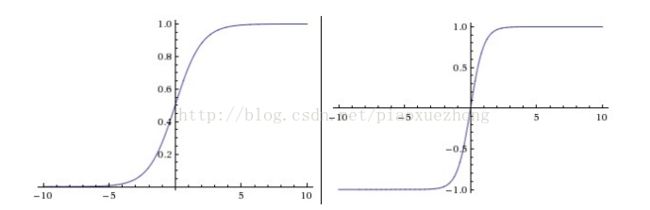
上图2中，左边是Sigmoid函数，它将输入范围压缩为[0,1]。右边是tanh函数，它将输入范围压缩为[-1,1]。

现在sigmoid函数已经很少使用了，因为sigmoid存在两个主要缺点：
（1）sigmoid函数饱和会使得梯度消失。当神经元的激活状态在接近于0或1时会产生饱和，此处的梯度几乎为0，而在反向传播中需要将这个（局部）梯度与整个损失函数关于该门单元输出的梯度相乘。所以如果这个局部梯度非常小的话，相乘的结果会接近于0。另外为了防止饱和现象，需要对权重矩阵的初始化特别注意。例如，当初始权重过大时，此时大多数神经元将会饱和，导致整个网络几乎不会学习了。
（2）sigmoid函数的输出不是以0为中心。神经元得到的数据不以0为中心，会影响梯度下降的计算。如果输入神经元的数据总是正数（比如在 中，每个元素x都大于0），那么权重 w 的梯度在反向传播的过程中将会出现要么全是正数，要么全是负数的现象，而这会导致梯度下降过程中权重的更新出现 “Z” 字型下降。当然，对整个数据的梯度累加后，权重将会有正有负，从而减弱上述问题。

对比之下，tanh函数也存在饱和现象，当时其输出是以0为中心的；

（3）ReLU函数：  

（4）Leaky ReLU函数：  

（5）Maxout函数：  

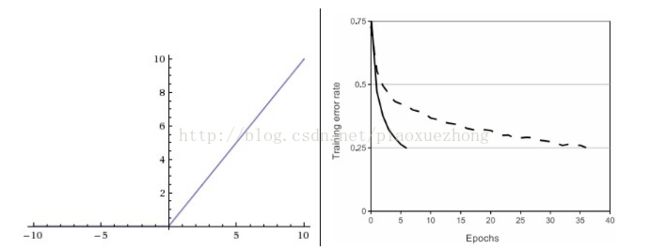
上图2左面是ReLU函数曲线，右边是ReLU函数相比于tanh函数在收敛性上的优势（Krizhevsky 等的论文指出ReLU收敛性能是tan的6倍），这是ReLU函数的优点，还有就是计算效率高，因为它只与0作比较。但是，ReLU函数也存在明显的缺点：当一个很大的梯度流过ReLU神经元时，可能会导致神经元无法被其他数据点再次激活，此时流过这个神经元的梯度都将会变成0，从而导致数据多样化的丢失。例如当学习率设置的过高后，可能会使得网络中40%的神经元死掉。

Leaky ReLU是一种为解决“ReLU死亡”问题的尝试：当x<0时，ReLU函数值为0，而Leaky ReLU给出一个很小的负数梯度值（如0.01）。有些论文指出这个函数的表现不错，但是效果不是很稳定。何凯明等人在2015年发布的论文Delving Deep into Rectifiers中介绍了一种新方法：PReLU，该方法把负值区间上的斜率作为每个神经元的一个参数，然而该函数在面对不同任务时是否都取得有益性方面（即一致性）没有清晰的说明。

Maxout函数是对ReLU和leaky ReLU函数的一般化归纳，ReLU和Leaky ReLU函数可以看作是Maxout函数的特例（当w1=0,b1=0时，就是ReLU）。这样Maxout神经元就只得到ReLU的优点，而摒弃了缺点，但是参数数量上却增加了。

神经网络的结构

分层组织

神经网络模型看成是神经元的集合，神经元之间以无环图的形式进行连接，即一些神经元的输出是另一些神经元的输入，但在网络中不允许循环结构出现，因为循环结构会导致前向传播的无限循环。通常神经网络模型结构是分层的，而不是像生物神经元那种聚合在一起的团状。最普通的分结构是全连接层（fully-connected layer），全连接层的某一层神经元与前后两层的神经元完全成对连接，但在同一层内的神经元之间没有连接。如下图所示：

左边是一个2层神经网络，隐层由4个神经元（或叫unit）组成，输出层由2个神经元组成，输入层是3个神经元；右边是一个3层神经网络。当说到N层神经网络时，输入层是不算入的。

左边网络有4+2=6个神经元（输入层不算在内），[3x4]+[4x2]=20个权重，4+2=6个偏置，共26个学习参数。
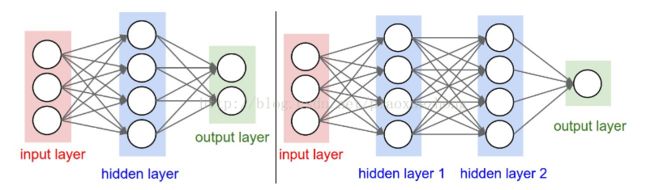
右边网络有4+4+1=9个神经元，[3x4]+[4x4]+[4x1]=32个权重，4+4+1=9个偏置，共41个学习参数。

前向传播计算实例：

将神经网络组织成层状的一个主要原因是这种结构可以让神经网络算法使用矩阵操作，从而变得简单、高效。在上图右边那个3层神经网络中，输入是一个[3x1]的向量，第一个隐层的权重W1是[4x3]的矩阵，所有单元的偏置为大小[4x1]的向量b1。这样，每个神经元的权重都在W1的一个行中，矩阵乘法：np.dot(W1, x) 可以计算出该层所有神经元的激活结果。同样W2将会是一个存储第二个隐层连接的[4x4]的矩阵，W3是用于输出层的[1x4]的矩阵。完整3层神经网络的前向传播就是简单的3次矩阵乘法运算，其中包含激活函数的使用。

# 一个3层神经网络的前向传播:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # 激活函数(用的sigmoid)
x = np.random.randn(3, 1)   # 含3个数字的随机输入向量(3x1)
h1 = f(np.dot(W1, x) + b1)  # 计算第一个隐层的激活数据(4x1)
h2 = f(np.dot(W2, h1) + b2) # 计算第二个隐层的激活数据(4x1)
out = np.dot(W3, h2) + b3   # 神经元输出(1x1)

代码中的  x 并不一定是一个单独的列向量，也可以是一个批量的训练数据（每个输入样本作为x的一列），所有样本可以并行计算。

神经网络的函数表达及尺寸设置：

研究证明，神经网络可以近似地表示任何连续函数，并且实践表明，多层神经网络效果要比单层效果好。在面对一个具体问题时，网络结构怎么确定呢？是不用隐层呢？还是一个隐层，两个隐层或更多？每个层的尺寸该多大？

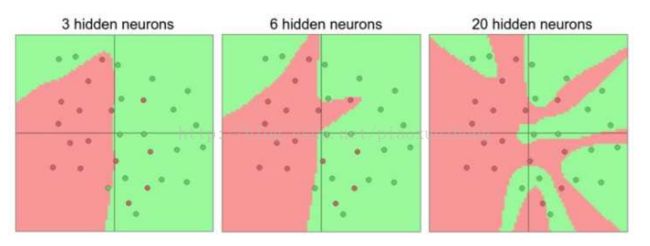
例如，在二维平面上的二分类问题, 链接的网页是该问题的demo。分别训练3个不同的神经网络，每个网络都只有一个隐层，但是每层的神经元数目不同。下图3是课程给出的不同数量神经元对应的分类结果：

当神经网络有更多的神经元时，可以表达更复杂的函数，但不足是可能造成对训练数据的过拟合。相反地，神经网络神经元数量太小会增加梯度下降的训练难度，另外最终的损失值可能展现出多变性。所以，在过拟合和泛化能力之间需要一个平衡，以及需要使用防止过拟合的方法以便可以运用多神经元结构。课中提到了正则化的方法，估计后面还会展开吧，留意一下。

参考：

http://cs231n.github.io/neural-networks-1/

https://zhuanlan.zhihu.com/p/21462488?refer=intelligentunit

https://zhuanlan.zhihu.com/p/21513367?refer=intelligentunit