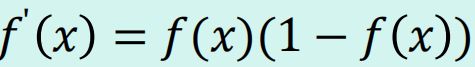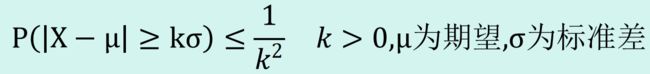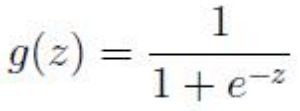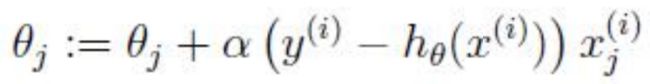福利网站！程序员面试——算法工程师面试大全第一部分

1. SGD,Momentum,Adagard,Adam 原理

SGD 为随机梯度下降,每一次迭代计算数据集的 mini-batch 的梯度,然后对参数进行跟新.

Momentum 参考了物理中动量的概念,前几次的梯度也会参与到当前的计算中,但是前几轮的 梯度叠加在当前计算中会有一定的衰减.

Adagard 在训练的过程中可以自动变更学习的速率,设置一个全局的学习率,而实际的学习 率与以往的参数模和的开方成反比.

Adam 利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率,在经过偏置的校正 后,每一次迭代后的学习率都有个确定的范围,使得参数较为平稳.

 

2.L1 不可导的时候该怎么办

当损失函数不可导,梯度下降不再有效,可以使用坐标轴下降法,梯度下降是沿着 当前点的负梯度方向进行参数更新,而坐标轴下降法是沿着坐标轴的方向,假设有 m 个特征个数, 坐标轴下降法进参数更新的时候,先固定 m-1 个值,然后再求另外一个的局部最优解,从而避免损 失函数不可导问题. 使用 Proximal Algorithm 对 L1 进行求解,此方法是去优化损失函数上界结果.

 

3.sigmoid 函数特性

定义域为( − ∞, + ∞)

值域为(-1,1)

函数在定义域内为连续和光滑的函数 处处可导,

导数为݂

 

4.切比雪夫不等式

 

5.最大似然估计和最大后验概率的区别?

最大似然估计提供了一种给定观察数据来评估模型参数的方法,而最大似然估计中的采样满 足所有采样都是独立同分布的假设.最大后验概率是根据经验数据获难以观察量的点估计,与最大似然估计最大的不同是最大后验概率融入了要估计量的先验分布在其中,所以最大后验概率可 以看做规则化的最大似然估计. 

 

6.概率和似然的区别

概率是指在给定参数θ的情况下,样本的随机向量 X=x 的可能性.而似然表示的是在给定样 本 X=x 的情况下,参数θ为真实值的可能性.一般情况,对随机变量的取值用概率表示.而在非贝叶斯统计的情况下,参数为一个实数而不是随机变量,一般用似然来表示.

 

7.频率学派和贝叶斯学派的区别

频率派认为抽样是无限的,在无限的抽样中,对于决策的规则可以很精确.贝叶斯派认为世界 无时无刻不在改变,未知的变量和事件都有一定的概率,即后验概率是先验概率的修正.频率派认为模型参数是固定的,一个模型在无数次抽样后,参数是不变的.而贝叶斯学派认为数据才是固定的而参数并不是.频率派认为模型不存在先验而贝叶斯派认为模型存在先验.

 

8.Lasso 的损失函数

 

9.Sfit 特征提取和匹配的具体步骤

生成高斯差分金字塔,尺度空间构建,空间极值点检测,稳定关键点的精确定位,稳定关键点，方向信息分配,关键点描述,特征点匹配 

 

10.欧拉公式

 

11.矩阵正定性的判断,Hessian 矩阵正定性在梯度下降中的应用

若矩阵所有特征值均不小于 0,则判定为半正定.若矩阵所有特征值均大于 0,则判定为正定. 在判断优化算法的可行性时Hessian矩阵的正定性起到了很大的作用,若Hessian正定,则函数的 二阶偏导恒大于 0,函数的变化率处于递增状态,在牛顿法等梯度下降的方法中,Hessian 矩阵的 正定性可以很容易的判断函数是否可收敛到局部或全局最优解.

 

12.讲一下 PCA

PCA 是比较常见的线性降维方法,通过线性投影将高维数据映射到低维数据中,所期望的是在投影的维度上,新特征自身的方差尽量大,方差越大特征越有效,尽量使产生的新特征间的相关性越小.PCA 算法的具体操作为对所有的样本进行中心化操作,计算样本的协方差矩阵,然后对协方差矩阵做特征值分解,取最大的 n 个特征值对应的特征向量构造投影矩阵.

 

13.拟牛顿法的原理

牛顿法的收敛速度快,迭代次数少,但是 Hessian 矩阵很稠密时,每次迭代的计算量很大,随 着数据规模增大,Hessian 矩阵也会变大,需要更多的存储空间以及计算量.拟牛顿法就是在牛顿 法的基础上引入了Hessian矩阵的近似矩阵,避免了每次都计算Hessian矩阵的逆,在拟牛顿法中, 用Hessian矩阵的逆矩阵来代替Hessian矩阵,虽然不能像牛顿法那样保证最优化的方向,但其逆 矩阵始终是正定的,因此算法始终朝最优化的方向搜索.

 

14.交叉熵公式

交叉熵：设 p(x),q(x)是 X 中取值的两个概率分布,则 p 对 q 的相对熵是：

在一定程度上,相对熵可以度量两个随机变量的“距离”,且有 D(p||q) ≠D(q||p).另外, 值得一提的是,D(p||q)是必然大于等于 0 的.

互信息：两个随机变量 X,Y 的互信息定义为 X,Y 的联合分布和各自独立分布乘积的相对熵, 用 I(X,Y)表示：

且有 I(X,Y)=D(P(X,Y)||P(X)P(Y)).下面,咱们来计算下 H(Y)-I(X,Y)的结果,如下： 

 

15.LR 公式

逻辑回归本质上是线性回归,只是在特征到结果的映射中加入了一层逻辑函数 g(z),即先 把特征线性求和,然后使用函数 g(z)作为假设函数来预测.g(z)可以将连续值映射到 0 和 1. g(z)为 sigmoid function.

则

sigmoid function 的导数如下：

 

 逻辑回归用来分类 0/1 问题,也就是预测结果属于 0 或者 1 的二值分类问题.这里假设了 二值满足伯努利分布,也就是

其也可以写成如下的形式：

对于训练数据集,特征数据 x={x1, x2, … , xm}和对应的分类标签 y={y1, y2, … , ym}, 假设 m 个样本是相互独立的,那么,极大似然函数为：

log 似然为：

如何使其最大呢?与线性回归类似,我们使用梯度上升的方法(求最小使用梯度下降),那 么 

 如果只用一个训练样例(x,y),采用随机梯度上升规则,那么随机梯度上升更新规则为：