Dijkstra算法及其堆优化
- 前言
- 算法作用
- 算法原理
- 算法结果
- 算法实现
- 朴素方法
- 堆优化
- 例题
- P3371 模板单源最短路径
- 题目描述
- 输入输出格式
- 输入格式
- 输出格式
- 输入输出样例
- 输入样例1
- 输出样例1
- 说明
- 时空限制
- 数据规模
- 样例说明
- P3371 模板单源最短路径
- 后记
前言
欢迎来到NOIP考前复习系列。。。。。。今天要讲的是Dijkstra。。。
当然,如果有任何错误的话,欢迎留言指出哟。。。
算法作用
Dijkstra算法用于解决单源最短路问题,即求取从一个给定的起点出发到其他节点的最短距离。
算法原理
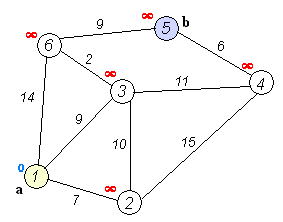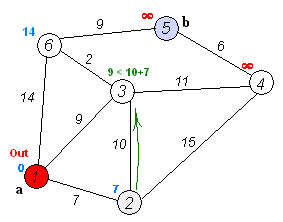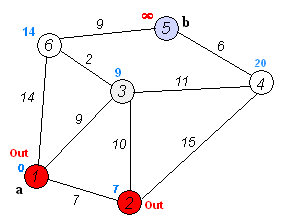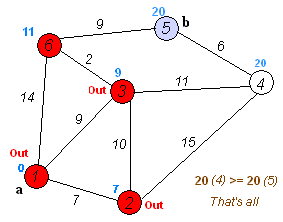
如图:
【上图转载自华山大师兄 最短路径—Dijkstra算法和Floyd算法】
我们首先定义一个数组 d ,代表我们选定的起点到其他各个点的距离最小值。
然后,将 d 数组中除了起点以外的所有的元素都赋成INF(无限大)。
然后开始扫描起点所连接的点,找出一个直接距离最短的点,加入已生成的树中,并将连接它们的这条边加入最小生成树中。
然后继续,从已有的最小生成树中的所有点出发,找到一个距离最近的,继续加入生成树。
算法结果
算法运行结束后,将会得到一个处理好的数组 d ,其中 d[i] 代表从起点出发到节点 i 的最短路长度。
算法实现
朴素方法
这个普通的写法我并不想过多介绍,因为这样做太过于普通,效率非常低。
你可以使用邻接矩阵来存储整个图,然后每次枚举对应的行或列来找到一个距离最近的。
代码也比较简单,这里并不想过多描述。事实上,我一开始就写的堆优化,因此再把它改成朴素算法将会比较多余。
堆优化
堆优化的主要思想就是使用一个优先队列(就是每次弹出的元素一定是整个队列中最小的元素)来代替最近距离的查找,用邻接表代替邻接矩阵,这样可以大幅度节约时间开销。
在这里有几个细节需要处理:
- 首先来讲,优先队列的数据类型应该是怎样的呢?
我们知道优先队列应该用于快速寻找距离最近的点。由于优先队列只是将最小的那个元素排在前面,因此我们应该定义一种数据类型,使得它包含该节点的编号以及该节点当前与起点的距离。
- 我们应该在什么时候对队列进行操作呢?
队列操作的地方,首先就是搜索刚开始,要为起点赋初始值,此时必须将起点加入优先队列中。该队列元素的节点编号为起点的编号,该节点当前与起点的距离为 0 。
- 那么如果一个节点到起点的最短距离通过其他的运算流程发生了变化,那么如何处理队列中的那个已经存入的元素?
事实上,你不需要理会队列中的元素,而是再存入一个就行了。因为如果要发生变化,只能将节点与起点之间的距离变得更小,而优先队列恰好是先让最小的那个弹出。
因此,轮到某一个队列元素弹出的时候,如果有多个元素的节点编号相同,那么被弹出的一定是节点编号最小的一个。等到后面再遇到这个节点编号的时候,我们只需要将它忽略掉就行了。
例题
洛谷P3371 【模板】单源最短路径
P3371 【模板】单源最短路径
题目描述
如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
输入输出格式
输入格式:
第一行包含三个整数N、M、S,分别表示点的个数、有向边的个数、出发点的编号。
接下来M行每行包含三个整数Fi、Gi、Wi,分别表示第i条有向边的出发点、目标点和长度。
输出格式:
一行,包含N个用空格分隔的整数,其中第i个整数表示从点S出发到点i的最短路径长度(若S=i则最短路径长度为0,若从点S无法到达点i,则最短路径长度为2147483647)
输入输出样例
输入样例#1:
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4输出样例#1:
0 2 4 3
说明
时空限制:
1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=15
对于40%的数据:N<=100,M<=10000
对于70%的数据:N<=1000,M<=100000
对于100%的数据:N<=10000,M<=500000
样例说明:
这个题就是模板题,直接打好Dijkstra就行了。
#includeq;
bool vis[MAXN+5];
void process()
{
for(int i=1;i<=n;i++) dist[i]=INF;
dist[s]=0;
q.push((qbase){s,0});
while(!q.empty())
{
qbase h=q.top();q.pop();
int hk=h.key,hv=h.value;
if(vis[hk]) continue;
vis[hk]=true;
for(int i=head[hk];i>0;i=edge[i].next)
{
int v=edge[i].v,w=edge[i].w;
if(!vis[v]&&dist[v]>hv+w)
{
dist[v]=hv+w;
q.push((qbase){v,dist[v]});
}
}
}
}
};
Dijkstra content;
int dist[MAXN+5];
int main()
{
int n,m,s;
scanf("%d%d%d",&n,&m,&s);
content.init(n,m,s,dist);
for(int i=1;i<=m;i++)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
content.credge(u,v,w);
}
content.process();
for(int i=1;i<=n;i++) printf("%d ",dist[i]==INF?2147483647:dist[i]);
return 0;
} 后记
坑已填。【理直气壮】