二、基于MATLAB的数字图像处理————空间滤波
（二）、基于MATLAB的数字图像处理————空间滤波
空间滤波也叫领域处理，空间卷积。
步骤：a，选择中心点f（x,y）;
b, 对该点领域内的像素进行计算；
c，计算的结果即为该点的响应
d，移动中心点，实现对像素的每个点的处理
根据计算方法的线性与非线性，分为线性空间滤波和非线性空间滤波两种。
1,线性空间滤波
对于步骤b，我们可以定义一个m*n的w矩阵，称之为滤波器，或者滤波模板。在整个图像f中逐点移动滤波器，滤波器在该点的响应就是滤波模板限定的领域内元素与滤波器的系数乘积之和。数学公式表示为：
其中a=(m-1)/2,b=(n-1)/2;一般吗，m,n为了计算方便都取奇数。
上述公式是相关计算，相应的还有卷积运算。区别在于，只不过在w通过f之前先将其旋转180°。公式如下：
MTLAB中的相关函数：
（1）imfilter//实现相关以及卷积运算
语法为：
g=imfilter(f,w,filtering_mode,boundary_options,size_options)
其中filtering_mode默认为相关，对卷积的规定为*‘conv’*；boundary_options是处理边界填充问题,默认为输入图像的边界用值0来填充，'replicate’复制图像边界外的值来扩展，'symmetric’通过边界镜像反射来扩展；size_options存在两种情况，‘same’,‘full’。
空间线性平均滤波的例子：
clear all
>> w=ones(31);
>> w=w./(31*31);
>> f=imread('C:/experiment/test5.jpg');
>> gd=imfilter(f,w);
>> imshow(gd,[]);
>> figure,imshow(f);
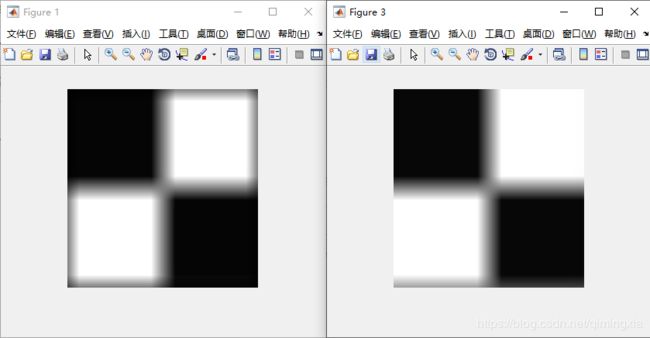
运行结果如下：
我们发现经过滤波过后，图像黑白边缘被模糊了，并且填充的边界是黑色的。这时改变boundary_options的状态，选择’replicate’。
gk=imfilter(f,w,'replicate');
>> figure,imshow(gk);
观察对比图像，我们会发现外围边界情况得到了改善。
（2）fspecial//构建滤波器
正常滤波工作中我们需要实现各种各样的效果，所以需要有各种各样的滤波器，我们可以借助fspecial函数来完成。
语法为：
w=fspecial(‘type’,parameters)
其中*‘type’*为滤波器的类型，parameters指相应的参数。
type=‘average’，为均值滤波，参数为n，代表模版尺寸，用向量表示，默认值为[3,3]。
type= ‘gaussian’，为高斯低通滤波器，参数有两个，n表示模版尺寸，默认值为[3,3]，sigma表示滤波器的标准差，单位为像素，默认值为 0.5。
type= ‘laplacian’，为拉普拉斯算子，参数为alpha，用于控制拉普拉斯算子的形状，取值范围为[0,1]，默认值为0.2。
type= ‘log’，为拉普拉斯高斯算子，参数有两个，n表示模版尺寸，默认值为[3,3]，sigma为滤波器的标准差，单位为像素，默认值为0.5
type= ‘prewitt’，为prewitt算子，用于边缘增强，无参数。
type= ‘sobel’，为著名的sobel算子，用于边缘提取，无参数。
type= ‘unsharp’，为对比度增强滤波器，参数alpha用于控制滤波器的形状，范围为[0,1]，默认值为0.2。
上个例子中，我们使用函数ones（31）来生成一个3131的二维矩阵，再将w除以(3131)得到平均滤波器。这里我们直接使用fspecial函数来得到平均滤波器。
w=fspecial('average',[31,31]);
>> f=imread('C:/experiment/test5.jpg');
>> gd=imfilter(f,w);
>> imshow(gd,[]);
很显然，两者的结果是一样的。我们可以使用fspecial 生成各种我们需要的线性空间滤波器。
2，非线性空间滤波
非线性滤波与线性滤波的区别在于，步骤b中的运算是非线性的。这里我们做一个统计排序滤波器的实验。
MATLAB的相关函数：
ordfilt2//计算统计排序滤波器的函数
语法：g=ordfilt2(f,order,domain)
函数通过使用领域的排序集合中第order个元素去代替f中的每个元素，来得到图像g，其中邻域由domain内的非0元素指定。domain是一个由0和1组成的mn的矩阵。
实现一个大小为mn的最小滤波器（一个排序集合中的第一个样本值）：
g=ordfilt2(f,1,ones(m,n))
实现一个大小为m*n的最大滤波器（一个排序集合中的最后一个样本值）：
g=ordfilt2(f,m*n,ones(m,n))
实现中值滤波器：
g=ordfilt2(f,(m*n+1)/2,ones(m,n))
中值滤波器还有一种实现方式：
g=medfilt2(f,[m n],padopt)
其中，[m n]为定义的m*n邻域，默认为3乘3领域；
padopt为指定三种可能的边界填充方式：默认’zeros’用0填充，'symmetric’按照原图像的镜像反射方式填充，'indexed’表示若f是double类就用1填充，否则用0。
中值滤波能够有效抑制椒盐噪声，试用中值滤波器对椒盐噪声进行处理实验。
f=imread('C:/experiment/test6.jpg');
>> f=rgb2gray(f);
>> imshow(f);
>> g=medfilt2(f);
>> figure,imshow(g);
实验结果显示，中值滤波确实能够抑制一定程度的椒盐噪声。