图形学笔记（八）——针孔照相机模型与照相机标定

python图像处理笔记-八-针孔照相机模型与照相机标定

前几天去忙别的事情了，大概有一个周没有更新了，周末有时间了赶紧学一手。这里对应的是书中的第四章
，能坚持到这里的话，就已经啃完了书的三分之一了。

参考教材：

• python计算机视觉编程
• 视觉SLAM十四讲，从理论到实践

针孔照相机模型

针孔摄像机模型（有时称作摄影照相机模型），是计算机视觉中广泛应用的照相机模型。原因是：

• 简单
• 精度足够

这个名字来源于一种简单的照相机，他利用小孔成像原理进行成像，换句话说就是：在光线投影到图像平面前，从唯一一个点经过，这个经过的点就叫做：照相机中心，记做C，如下图所示：

（这张图来自于他人博客：https://blog.csdn.net/Dujing2019/article/details/91691202）

不同之处在于，在现实世界中，我们的图像平面在相机中心之后，而这里，我们为了方便理解，将
点放在了成像平面之前。如果图像坐标轴和三维坐标系中中x、y轴对齐、平行的话，可以得出针孔照相机的投影性质。照相机的光学坐标轴和z轴一致，该投影几何可以简化成相似三角形。在头硬质前通过旋转和平移变换，对该坐标系加入三维点，会出现完整的投影变换。

在针孔照相机中，三维点X为图像点x，它们之间的关系如下所示（都是其次坐标）：
$$\lambda x=PX$$
这里，3*4的矩阵P是照相机矩阵（投影矩阵），齐次坐标中，三维点X的坐标由四个元素组成，$X=[X,Y,Z,W]$，这里的标量$\lambda$为三维点的逆深度。如果我们想要在齐次坐标中将最后一个值归一化为1那么我们需要他。

照相机矩阵

也就是上面说的P，这个P可以再一步分解：
$$P=K[R|t]$$
在上一个章节中我们对此也有所接触，我们知道，在射影变换矩阵中，左上角四个元素负责控制图像的旋转、缩放等，而右边的两个元素负责控制图像的平移。这里也是同理。

但不同的是，这里同的是，这里多出了一个矩阵K，这个矩阵K叫做内标定矩阵，它描述的是照相机投影的性质，标定矩阵仅和照相机自身的情况有关，通常可以写作：
$$K=\left[\begin{array}{ccc}af& s& c_x\\ 0& f& c_y\\ 0& 0& 1\end{array}\right]$$

图像平面和照相机之间的焦距为f，当像素数组在传感器上偏斜的时候，需要用到倾斜参数s。大多数情况下，s可以设置为0，也就是说:
$$K=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$
其中，s被我们定成了0，$f_x=a{f}_y$，那么话再说回来，$f_x,f_y$的不同是用a来度量的，它叫做：纵横比例参数。a是在像素元素非正方形的时候使用的，通常情况下，我们可以设置$a=1$，经过了这些假设，矩阵变成了：
$$K=\left[\begin{array}{ccc}f& 0& c_x\\ 0& f& c_y\\ 0& 0& 1\end{array}\right]$$
除了焦距之外，标定矩阵中剩余的唯一参数为光心（也叫主点），他的坐标是：$(c_x,c_y)$，它代表着光线坐标轴和图像平面的交点。因为光心通常在图像的中心，并且图像的坐标是从左上角开始的，所以光心的坐标非常接近于图像宽度和高度的一半。

三维点的投影

from scipy import linalg
from numpy import *
from pylab import *

class Camera(object):
    """
    表示针孔照相机的类
    """

    def __init__(self, P):
        """
        初始化照相机模型
        :param P: P = K[R| t]
        """
        self.P = P
        self.K = None # 标定矩阵
        self.R = None # 旋转
        self.t = None # 平移
        self.c = None # 照相机中心
    
    def project(self, X):
        """
        返回投影到图像视图的点
        :param X:X (4*n数组)的投影点
        :return:并且进行坐标归一化
        """
        x = dot(self.P, X)
        for i in range(3):
            x[i] /= x[2]
        return x

if __name__ == "__main__":

    # 载入点
    points = loadtxt("house.p3d")
    # 交换维度以读取
    points = points.swapaxes(0,1)
    # 齐次坐标
    points = vstack((points,ones(points.shape[1])))
    # 设置照相机参数
    P = hstack((eye(3), array([[0],[0],[-10]])))
    cam = Camera(P)
    x = cam.project(points)

    # 绘制投影
    figure()
    plot(x[0], x[1], 'k.')
    show()

我们使用牛津多视图数据集中的ModelHousing数据集来运行，原书中的下载地址已经过时，如果想要下载，可以在：http://www.robots.ox.ac.uk/~vgg/data/mview/ 进行下载。

为了研究照相机的移动会如何改变投影效果，我们围绕一个随机的三维向量进行增量旋转的投影：

from scipy import linalg
import numpy as np
import matplotlib.pyplot as plt

class Camera(object):
    """
    表示针孔照相机的类
    """

    def __init__(self, P):
        """
        初始化照相机模型
        :param P: P = K[R| t]
        """
        self.P = P
        self.K = None # 标定矩阵
        self.R = None # 旋转
        self.t = None # 平移
        self.c = None # 照相机中心
    
    def project(self, X):
        """
        返回投影到图像视图的点
        :param X:X (4*n数组)的投影点
        :return:并且进行坐标归一化
        """
        x = np.dot(self.P, X)
        for i in range(3):
            x[i] /= x[2]
        return x

    def rotationMatrix(self, a):
        """
        用于描述围绕a轴旋转的三维旋转矩阵
        :param a: 旋转轴
        """
        R = np.eye(4)
        R[:3, :3] = linalg.expm([[0, -a[2], a[1]], [a[2], 0, -a[0]], [-a[1], a[0], 0]])
        return R


if __name__ == "__main__":

    # 载入点
    points = np.loadtxt("house.p3d")
    # 交换维度以读取
    points = points.swapaxes(0,1)
    # 齐次坐标
    points = np.vstack((points,np.ones(points.shape[1])))
    # 设置照相机参数
    P = np.hstack((np.eye(3), np.array([[0],[0],[-10]])))
    cam = Camera(P)
    x = cam.project(points)

    # 绘制投影
    plt.figure()
    plt.plot(x[0], x[1], 'k.')
    plt.show()

    # 创建变换
    r = 0.05 * np.random.random(3)
    rot = cam.rotationMatrix(r)

    # 旋转矩阵和投影
    plt.figure()
    for t in range(100):
        cam.P = np.dot(cam.P, rot)
        x = cam.project(points)
        plt.plot(x[0], x[1], 'k.')
        plt.show()

最终模拟出的图片如下：

上面这张图代表点的运动轨迹，想画它非常简单：

plt.figure()
for t in range(20):
    cam.P = np.dot(cam.P, rot)
    x = cam.project(points)
    plt.plot(x[0], x[1], 'k.')
plt.show()

相当于我们每次都画，但是都不show，最后再一起show出来就可以了。

照相机矩阵的分解

没啥好讲的，贴代码

from scipy import linalg
import numpy as np
import matplotlib.pyplot as plt

class Camera(object):
    """
    表示针孔照相机的类
    """

    def __init__(self, P):
        """
        初始化照相机模型
        :param P: P = K[R| t]
        """
        self.P = P
        self.K = None # 标定矩阵
        self.R = None # 旋转
        self.t = None # 平移
        self.c = None # 照相机中心
    
    def project(self, X):
        """
        返回投影到图像视图的点
        :param X:X (4*n数组)的投影点
        :return:并且进行坐标归一化
        """
        x = np.dot(self.P, X)
        for i in range(3):
            x[i] /= x[2]
        return x

    def rotationMatrix(self, a):
        """
        用于描述围绕a轴旋转的三维旋转矩阵
        :param a: 旋转轴
        """
        R = np.eye(4)
        R[:3, :3] = linalg.expm([[0, -a[2], a[1]], [a[2], 0, -a[0]], [-a[1], a[0], 0]])
        return R


    def factor(self):
        """
        将矩阵分解为kRt，P = K[R|t]
        :return:KRt
        """
        # 分解前半部分
        K, R = linalg.rq(self.P[:,:3])
        # 将K的对角线元素设为正值
        T = np.diag(np.sign(np.diag(K)))
        if(linalg.det(T)<0):
            T[1, 1] *= -1
        self.K = np.dot(K, T)
        self.R = np.dot(T, R)
        self.t = np.dot(linalg.inv(self.K), self.P[:, 3])
        return self.K, self.R, self.t


if __name__ == "__main__":

    # 载入点
    points = np.loadtxt("house.p3d")
    # 交换维度以读取
    points = points.swapaxes(0,1)
    # 齐次坐标
    points = np.vstack((points,np.ones(points.shape[1])))
    # 设置照相机参数
    P = np.hstack((np.eye(3), np.array([[0],[0],[-10]])))
    cam = Camera(P)
    x = cam.project(points)

    # 绘制投影
    plt.figure()
    plt.plot(x[0], x[1], 'k.')
    plt.show()

    # 创建变换
    r = 0.05 * np.random.random(3)
    rot = cam.rotationMatrix(r)
    # 旋转矩阵和投影
    plt.figure()
    for t in range(20):
        cam.P = np.dot(cam.P, rot)
        x = cam.project(points)
        plt.plot(x[0], x[1], 'k.')
    plt.show()

    # 测试新写的函数
    K = np.array([[1000, 0, 500], [0, 1000, 300], [0, 0, 1]])
    tmp = cam.rotationMatrix([0, 0, 1])[:3, :3]
    Rt = np.hstack((tmp, np.array([[50], [40], [30]])))
    cam = Camera(np.dot(K, Rt))

    print(K,Rt)
    print(cam.factor())

你可以观测到，结果与输入并不相同，这是由于为了避免符号的二义性而导致的。

计算中心

照相机的中心是一个三维点，满足约束：$PC=0$，又因为$P=K[R|t]$，所以有:

KaTeX parse error: No such environment: align at position 9: \begin{̲a̲l̲i̲g̲n̲}̲ K [R|t] C = K…

实现起来就很简单了，当然我们也可以看出来照相机的中心和照相机的标定矩阵是无关的：

def center(self):
    """
        计算、返回摄像机的中心
        """
    if(self.c is not None):
        return self.c
    self.factor()
    self.c = -np.dot(self.R.T, self.t)
    return self.c

相机标定（张正友标定法）

标定是非常重要的一步，它起到了减少误差的作用。

传统的标定方法虽然可以用于任意的摄像机模型，并且精度较高。但其不足之处在于：过程过于复杂，需要高精度的已知结构信息，在实际应用中的很多场景下无法使用标定块，而基于主动视觉的摄像机自标定技术不能用于摄像机运动未知和无法控制的场景。

张正友标定法是一种介于传统标定方法和自标定方法之间的一种简易标定方法。它的标定方法简单易做，只需要我们打印一张棋盘格就可以了。并且在标定过程中只需要将平面模板按任意角度在摄像机前放置即可。

研究的坐标系

我们主要研究四个坐标系：

• 世界坐标系
• 相机坐标系
• 图像坐标系
• 像素坐标系

其中图像坐标系和像素坐标系非常相似，图像坐标系的原点是相机光轴与成像平面的角点，单位是毫米，而像素坐标系的原点是图像的左上角，像素坐标系的单位是像素。

世界坐标系到相机坐标系的变换

$$\left[\begin{array}{c}{X}_C\\ Y_C\\ Z_C\\ 1\end{array}\right]==\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$

这个就很简单了，就是一个旋转平移

相机坐标系下的点转换到图像坐标系下

$$x=\frac{f}{Z_c}{X}_c$$

$$y=\frac{f}{Z_c}{Y}_c$$

这个也非常的简单，我们可以用矩阵的形式来进行表达：
$$\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=.\left[\begin{array}{cccc}\frac{f}{Z_C}& 0& 0& 0\\ 0& \frac{f}{Z_C}& 0& 0\\ 0& 0& \frac{f}{Z_C}& 0\end{array}\right]\left[\begin{array}{c}{X}_C\\ Y_C\\ Z_C\\ 1\end{array}\right]$$

图像坐标系到像素坐标系的变换

$$u=c_x+x{f}_x$$

$$v=c_y+y{f}_y$$

$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=.\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

相机畸变模型

$$\begin{gathered} x_{distorted}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+2p_{1}xy+p_2(r^2+2x^2) \\ {y}_{distorted}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+2p_{2}xy+p_1(r^2+2y^2) \end{gathered}$$

想要知道是枕型畸变的话，那么离中心点越远，偏移量越大，反之则反。

标定了什么？

标定了两个部分：

• 内参：
  • $f_x,f_y$：相机焦距
  • $c_x,c_y$：图像中心点
  • $k_1,k_2,k_3,p_1,p_2$：畸变参数
• 外参：
  • $Rt$：反映了相机和世界坐标的关系

标定任务

我们可以将我们的标定结果用一个函数来衡量：
$${\Sigma }_{i=1}^n{\Sigma }_{j=1}^m||m_{ij}-\hat{m}(A,R_i,t_i,M_j)|{|}^2$$
说人话就是，我们计算出来的参数得到的像素坐标与真实像素坐标的差的平方的和。但是非常遗憾的是我们无法直接对该目标函数进行优化，因为需要优化的参数过多，非常容易陷入局部最优。于是张正友便提出了张正友标定法，该方法通过数值方法找到了一个很好的起始点。

标定原理

我们假设我们的平面处于世界坐标系下$Z=0$的平面内。需要注意的是：如果想用张正友标定法，那么就必须尽量保证标定板（也就是那个棋盘格的纸）必须在一个平面上，这样才能满足假设，标定板（标定平面）在世界坐标系下$Z=0$平面内。

当然，在满足这个条件的时候，我们就有如下公式：
$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=.A\left[\begin{array}{cccc}{r}_1& r_2& r_3& t\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 0\\ 1\end{array}\right]$$
其中:
$$A=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$
因为这个Z恒为0，所以r3是不会影响结果的，所以我们可以把式子写为：
$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=.A\left[\begin{array}{ccc}{r}_1& r_2& t\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]$$
在前面的学习中我们知道，如果知道两个平面上的点的映射关系，我们是可以把两个平面之间的单应性变换关系求出来的（如果你不懂可以看看之前的博客，有专门讲单应性变换的）

现在我们可以把式子写为：
$$sm=A\left[\begin{array}{ccc}{r}_1& r_2& t\end{array}\right]M$$
可以将右边的式子合并成：
$$sm=HM$$
其中,$H=A\left[\begin{array}{ccc}{r}_1& r_2& t\end{array}\right]$这里的H代表内参和外参的乘积构成的矩阵。我们可以通过反推单应性变换将H求出，那么现在的问题在于，如何通过已知的H反求出内参和外参。

我们知道，内参、外参、H之间是知二推一的关系，所以我们就想，如果能将内参求出来，那么就可以很自然的知道外参了。
$$\left[\begin{array}{ccc}{h}_1& h_2& h_3\end{array}\right]=\lambda A\left[\begin{array}{ccc}{r}_1& r_2& r_t\end{array}\right]$$
有以下约束条件：

• $r_1,r_2$正交，也就是$r_1{r}_2=0$。因为$r_1,r_2$是分别绕$x,y$轴得到的，而$x,y$轴垂直$z$轴。
• 旋转向量的模为1，也就是说$|r_1|,|r_2|=1$，这是因为旋转不改变尺度。

根据这两个约束条件，经过数学变换，可以得到:
$$h_1^T{A}^{-T}{A}^{-1}{h}_2=0$$

$$h_1^T{A}^{-T}{A}^{-1}{h}_1=h_2^T{A}^{-T}{A}^{-1}{h}_2$$

实际上这两个式子在表达：
$$\begin{gathered} r_1{r}_2=0 \\ {r}_1{r}_1=r_2{r}_2 \end{gathered}$$
我们用B来表示$A^{-T}{A}^{-1}$，可以写作：

可以看出来B是一个对称矩阵，所以B的有效元素只有六个：
$$b={\left[\begin{array}{cccccc}{B}_{11}& B_{12}& B_{22}& B_{13}& B_{23}& B_{33}\end{array}\right]}^T$$
我们可以将b理解为有关于相机内参的未知量，进一步化简可以得到：
$$h_i^{T}B{h}_j=v_{ij}^{T}b$$
通过计算可以得到：
$$v_{ij}={\left[\begin{array}{ccccc}{h}_{i1}hj1& h_{i1}{h}_{j2}+h_{i2}{h}_{j1}& h_{i2}{h}_{j2}& h_{i3}{h}_{j2}+h_{i2}{h}_{j3}& h_{i3}{h}_{j3}\end{array}\right]}^T$$
那么综合上面的信息，我们现在的任务就变成解方程：
$$\left[\begin{array}{c}{v}_{12}^T\\ (V_{11}-v_{22}{)}^T\end{array}\right]b=0$$
那么我们至少需要拍三张照片才能将内参矩阵确定出来，当然我们拍的照片越多，我们的抗噪声的能力也就越强。最后，我们根据结果，将内参的值提取出来就可。

然后也可以获得外部参数:

标定工具

有两种：

• 棋盘格
• 圆靶

理想状态下圆形的检测精度较高，因为它能避免特征检测时候的错误。也就是说：中心拟合精度高。但是圆形却存在着偏心差，如下图：

但是相比之下，棋盘格却不存在偏心差。

标定的摄像机位置和数量

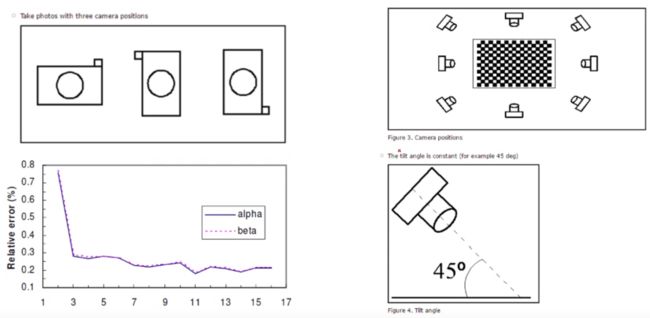
可以从这张图中看出来：

• 拍十张以上是比较好的，但是最少要拍三张
• 正常角度、旋转拍
• 从不同视角去拍标定板
• 尽量将标定板放在相机中心

等我写个程序再写一个标定的实操博客。