视频分析——Harris角点检测
文章目录
- 一、角点概念
- 1. 角点定义
- 2. 角点意义
- 3. 角点应用
- 4. 角点检测算法分类
- 4.1 基于灰度图像的角点检测
- 4.1.1 基于梯度
- 4.1.2基于模板
- ➰ Kitchen-Rosenfeld角点检测算法,
- ➰ Harris角点检测算法、
- ➰ KLT角点检测算法、
- ➰ SUSAN角点检测算法。
- 4.1.3 基于模板梯度组合
- 4.2 基于二值图像的角点检测
- 4.3 基于轮廓曲线的角点检测
- 4.3.1 计算角点强度k
- 4.3.2 计算曲线曲率的极值
- 4.3.3 多尺寸角点检测
- 二、工作原理
- 2.1 核心算法
- 2.2 数学表示
- 三、OpenCV的API
- 1. CornerHarris
- 2. C++实现
- 3. Python实现
一、角点概念
1. 角点定义
从图像分析的角度来定义角点可以有以下两种定义:
-
角点可以是两个边缘的角点;
角点通常被定义为两条边的交点。往往需要对图像边缘进行编码,这在很大程度上依赖于图像的分割与边缘提取,具有相当大的难度和计算量,且一旦待检测目标局部发生变化,很可能导致操作的失败。
-
角点是邻域内具有两个主方向的特征点;
角点的局部邻域应该具有两个不同区域的不同方向的边界。
2. 角点意义
角点是图像很重要的特征,对图像图形的理解和分析有很重要的作用。
角点在保留图像图形重要特征的同时,可以有效地减少信息的数据量,使其信息的含量很高,有效地提高了计算的速度,有利于图像的可靠匹配,使得实时处理成为可能。
3. 角点应用
在现实世界中,角点对应于物体的拐角,道路的十字路口、丁字路口等。
角点检测(Corner Detection)是计算机视觉系统中获取图像特征的一种方法,广泛应用于:
- 运动检测、
- 图像匹配、
- 视频跟踪、
- 三维重建、
- 目标识别等。
也可称为特征点检测。
4. 角点检测算法分类
百度百科
目前的角点检测算法可归纳为3类:
4.1 基于灰度图像的角点检测
基于灰度图像的角点检测又可分为:
-
4.1.1 基于梯度
基于梯度的方法是通过计算边缘的曲率来判断角点的存在性,角点计算数值的大小不仅与边缘强度有关,而且与边缘方向的变化率有关,该方法对噪声比基于模板的角点检测方法对噪声更为敏感。
通过计算基于梯度的算法来确定的角点是不合理的。
-
4.1.2基于模板
其中基于模板的方法主要考虑像素领域点的灰度变化,即图像亮度的变化,将与邻点亮度对比足够大的点定义为角点。
常见的基于模板的角点检测算法有:
➰ Kitchen-Rosenfeld角点检测算法,
➰ Harris角点检测算法、
➰ KLT角点检测算法、
➰ SUSAN角点检测算法。
和其他角点检测算法相比,SUSAN角点检测算法具有算法简单、位置准确、抗噪声能力强等特点。
-
4.1.3 基于模板梯度组合
除了直接对灰度图像的像素操作以外,采用变换的方法,用电磁场理论中矢势的鞍点检测来代替角点的检测,是一种综合了模板角点检测和灰度曲率角点检测的方法。
通过高斯模板和图像的卷积获得Canny边缘映射图,再计算梯度和边缘矢量就得到了矢势。对于矢势计算高斯曲率和平均曲率来判定是否是鞍点,对应的应该是图像的角点。因为涉及到了曲率的计算,也有人将该方法归到边缘曲线的角点检测。
4.2 基于二值图像的角点检测
刘文予等人提出一种基于形态骨架的角点检测方法,该方法将原始图像看作一个多边形,则多边形的角点一定在骨架的延长线上,且角点所对应的骨架点的最大圆盘半径应该趋于0,检测骨架中的最大圆盘为0的点,即为角点。
因为在二值图像阶段处理,计算量并不是很大,所以保证了计算的实时性。
应该指出的是,虽然将二值图像作为一个单独的检测目标列出来,但是基于灰度图像的各种处理方法对此仍然有效。
二值图像处于灰度和边缘轮廓图像的中间步骤,所以专门针对此类图像的角点检测方法并不多见。
4.3 基于轮廓曲线的角点检测
-
4.3.1 计算角点强度k
通过计算角点强度k来提取角点,这种方法虽然简单,但容易受噪声干扰,效果不是很理想。
为了将干扰去除,减少边缘毛刺干扰,Asada等人提出首先对边缘采用高斯平滑,即减少了将局部弯曲度突然增大而误判为角点的概率。但角点强度k是预先确定还是根据曲线的弯曲度自适应调节,对于检测的结果影响很大。
-
4.3.2 计算曲线曲率的极值
对于曲线曲率的计算,一种是直接对离散的曲线进行计算,另一种是用某类函数对原始曲线分段拟合,然后根据拟合后的曲线分段方程,计算曲线曲率极值得到角点的位置。
-
4.3.3 多尺寸角点检测
在曲线尺度空间中,随着曲线尺度由小变大,一直保持较高弯曲度的点必定是所要求取的角点。
二、工作原理
Harris 角点检测子
2.1 核心算法
因为角点是两个边缘的连接点,它代表了两个边缘变化的方向上的点。图像渐变有很高的变化。这种变化是可以帮助检测角点的。
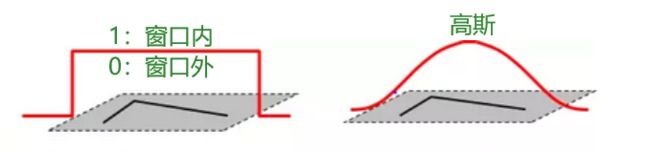
算法核心:
利用局部窗口在图像上进行移动判断灰度发生较大的变化,如果在各个方向上移动这个特征的小窗口,窗口内区域的灰度发生了较大的变化,那么就认为在窗口内遇到了角点。
根据下面三幅图可以清晰理解角点检测的过程:
⭕平坦区域
窗口在各个方向上移动,梯度都没有变化。
⭕边缘区域
窗口在某个方向上没有变化,另一个方向上有明显变化,那么,这块区域可能存在边缘。
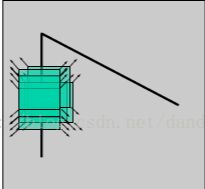
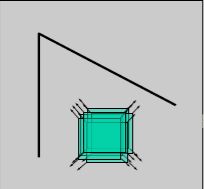
⭕角度边缘
窗口在各个方向上灰度发生了较大的变化,那么,这块区域可能存在角点。
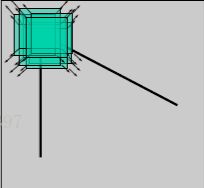
Harris角点检测正是利用了这个直观的物理现象,通过窗口在各个方向上的变化程度,决定是否为角点。
2.2 数学表示
根据算法思想,构建数学模型,计算移动窗口的的灰度差值。
由于角点代表了图像像素梯度变化,我们将寻找这个”变化”。
-
将窗口向各个方向 移动 [ u , v ] [u , v] [u,v],计算所有差异的总和,即灰度的变化 E ( u , v ) E(u,v) E(u,v)。
E ( u , v ) = ∑ x , y w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] 2 E(u,v)= \sum_{x,y}w(x,y)[I(x + u,y + v)-I(x,y)] ^ {2} E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2
其中:
w ( x , y ) w(x,y) w(x,y) 表示窗口函数
I ( x , y ) I(x,y) I(x,y) 表示 [ x , y ] [x,y] [x,y]处的图像灰度
I ( x + u , y + v ) I(x+u,y+v) I(x+u,y+v)是窗口平移到 [ x + u , y + v ] [x+u,y+v] [x+u,y+v]处的图像灰度 -
为了寻找带角点的窗口,我们搜索像素灰度变化较大的窗口。于是, 我们期望最大化以下式子:
∑ x , y [ I ( x + u , y + v ) − I ( x , y ) ] 2 \sum_{x,y}[ I(x+u,y+v) - I(x,y)]^{2} x,y∑[I(x+u,y+v)−I(x,y)]2 -
为了减小计算量,使用 泰勒(Taylor)展开式:
E ( u , v ) ≈ ∑ x , y [ I ( x , y ) + u I x + v I y − I ( x , y ) ] 2 E(u,v) \approx \sum_{x,y}[ I(x,y) + u I_{x} + vI_{y} - I(x,y)]^{2} E(u,v)≈x,y∑[I(x,y)+uIx+vIy−I(x,y)]2 -
式子可以展开为:
E ( u , v ) ≈ ∑ x , y u 2 I x 2 + 2 u v I x I y + v 2 I y 2 E(u,v) \approx \sum_{x,y} u^{2}I_{x}^{2} + 2uvI_{x}I_{y} + v^{2}I_{y}^{2} E(u,v)≈x,y∑u2Ix2+2uvIxIy+v2Iy2 -
一个举证表达式可以写为:
E ( u , v ) ≈ [ u v ] ( ∑ x , y w ( x , y ) [ I x 2 I x I y I x I y I y 2 ] ) [ u v ] E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} \left ( \displaystyle \sum_{x,y} w(x,y) \begin{bmatrix} I_x^{2} & I_{x}I_{y} \\ I_xI_{y} & I_{y}^{2} \end{bmatrix} \right ) \begin{bmatrix} u \\ v \end{bmatrix} E(u,v)≈[uv](x,y∑w(x,y)[Ix2IxIyIxIyIy2])[uv] -
对于局部微小的移动量 [ u , v ] [u,v] [u,v],可以近似得到:
E ( u , v ) ≈ [ u v ] M [ u v ] E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} M \begin{bmatrix} u \\ v \end{bmatrix} E(u,v)≈[uv]M[uv] -
其中M是一个2×2矩阵,由图像的导数表示为:
M = ∑ x , y w ( x , y ) [ I x 2 I x I y I x I y I y 2 ] M = \displaystyle \sum_{x,y} w(x,y) \begin{bmatrix} I_x^{2} & I_{x}I_{y} \\ I_xI_{y} & I_{y}^{2} \end{bmatrix} M=x,y∑w(x,y)[Ix2IxIyIxIyIy2]
I x I_x Ix 和 I y I_y Iy 是图像在 x 和 y 方向的导数(可以用函数cv2.Sobel()计算得到)。矩阵M又称为Harris矩阵。
-
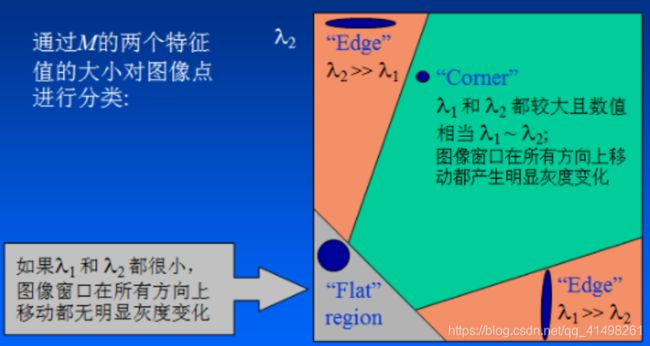
忽略余项之后的表达式为一个二项式函数,然而二项式函数的本质上就是一个椭圆函数,椭圆的扁率和尺寸是由M(x,y)的特征值λ1、λ2决定的,
椭圆的方向是由M(x,y)的特征矢量决定的,如下图所示,椭圆方程为:
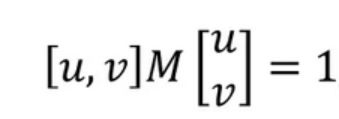

椭圆函数特征值与图像中的角点、直线(边缘)和平面之间的关系如下图所示。共可分为三种情况:- a. 图像中的直线。一个特征值大,另一个特征值小,λ1>λ2或λ2>λ1。自相关函数值在某一方向上大,在其他方向上小。
- b. 图像中的平面。两个特征值都小,且近似相等;自相关函数数值在各个方向上都小。
- c. 图像中的角点。两个特征值都大,且近似相等,自相关函数在所有方向都增大。
-
M为梯度的协方差矩阵 ,在实际应用中为了能够应用更好的编程,定义了角点响应函数R,通过判定R大小来判断像素是否为角点。R取决于M的特征值,对于角点|R|很大,平坦的区域|R|很小,边缘的R为负值。Harris角点检测算法就是对角点响应函数R进行阈值处理:R > threshold,即提取R的局部极大值。
R = d e t ( M ) − k ( t r a c e ( M ) ) 2 R = det(M) - k(trace(M))^{2} R=det(M)−k(trace(M))2
其中:
λ 1 和 λ 2 λ_1 和 λ_2 λ1和λ2是矩阵 M 的特征值。
d e t ( M ) = λ 1 λ 2 det(M) = \lambda_{1}\lambda_{2} det(M)=λ1λ2
t r a c e ( M ) = λ 1 + λ 2 trace(M) = \lambda_{1}+\lambda_{2} trace(M)=λ1+λ2
k为经验常数,一般取k=0.04~0.06。为了去除加权常数κ,我们通常使用商数 d e t M ( t r a c e M ) 2 \frac{detM}{(traceM)^2} (traceM)2detM作为指示器。

三、OpenCV的API
1. CornerHarris
-
说明
函数在图像上运行Harris角点检测。类似于 cornerMinEigenVal 和cornerEigenValsAndVecs函数,对于每一个像素 ( x , y ) (x,y) (x,y),它在块大小为blockSize×blockSize的邻域内计算出一个2×2的梯度协方差矩阵 M ( x , y ) M(x,y) M(x,y)。然后计算如下特征:
dst ( x , y ) = d e t M ( x , y ) − k ⋅ ( t r M ( x , y ) ) 2 \texttt{dst} (x,y) = \mathrm{det} M^{(x,y)} - k \cdot \left ( \mathrm{tr} M^{(x,y)} \right )^2 dst(x,y)=detM(x,y)−k⋅(trM(x,y))2
图像中的角点可以作为此响应映射的局部最大值。 -
函数
CV_EXPORTS_W void cornerHarris( InputArray src, OutputArray dst, int blockSize, int ksize, double k, int borderType = BORDER_DEFAULT ); Python: dst=cv.cornerHarris(src, blockSize, ksize, k[, dst[, borderType]] ) -
参数
src 输入的8位单通道灰度 或者 浮点型的图像。 dst 用于保存Harris角点检测结果。它的通道类型是CV_32FC1,大小和输入图像相同。 blockSize 滑块窗口的大小。 (详细参考 cornerEigenValsAndVecs).ksize Sobel边缘检测滤波器大小 k Harris角点检测自由参数。一般设置为0.04~0.06 borderType 插值类型,具体:BorderTypes
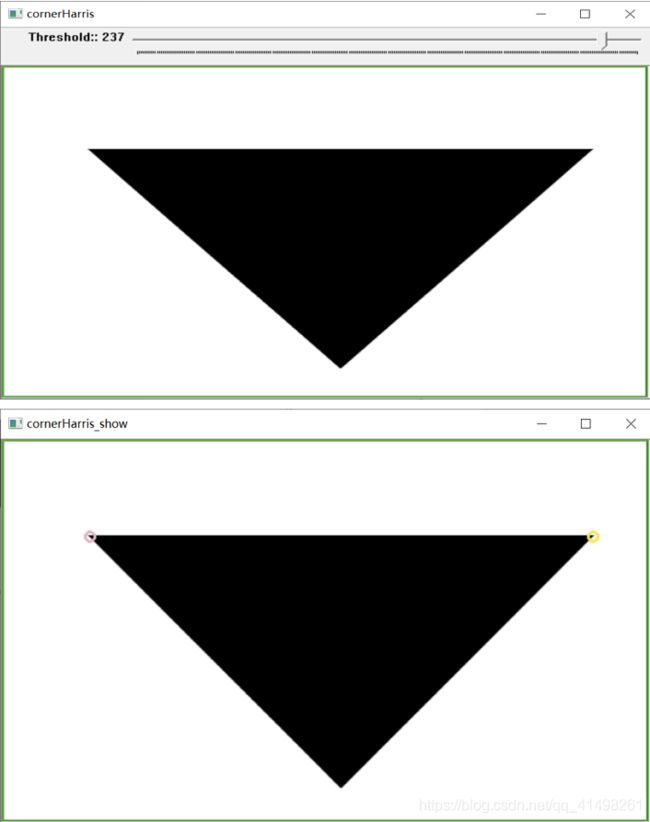
2. C++实现
Mat src_cornerHarris, gray_cornerHarris;
Mat copySrc;
int thresh = 200;
int max_thresh = 255;
RNG rng(12345);
String src_name = "cornerHarris";
String dst_name = "cornerHarris_show";
void cornerHarrisTest(int,void*){
src_cornerHarris = copySrc.clone();
//转化为灰度图像
Mat gray;
if (src_cornerHarris.channels() == 3) {
cvtColor(src_cornerHarris, gray, COLOR_BGR2GRAY);
}
else
{
gray = src_cornerHarris.clone();
}
//设置滑块窗口的大小
int blockSize = 2;
//设置Sobel边缘检测滤波器大小
int apertureSize = 3;
//Harris角点检测自由参数。一般设置为0.04~0.06
double k = 0.04;
//返回值其实就是R值构成的灰度图像,灰度图像坐标会与原图像对应
//存放的像素值R表示角点分数,当R值很大的时候,就可以认为这个点是一个角点
Mat dst = Mat::zeros(src_cornerHarris.size(), CV_32FC1);
//角点检测
cornerHarris(gray, dst, blockSize, apertureSize, k);
Mat dst_norm = Mat::zeros(dst.size(), dst.type());
//将角点分数值归一化到0—255范围内
normalize(dst, dst_norm, 0, 255, NORM_MINMAX,CV_32FC1,Mat());
convertScaleAbs(dst_norm, dst_norm);
//遍历每一个角点分数
for (size_t i = 0; i <dst.rows; i++)
{
for (size_t j= 0; j < dst.cols; j++)
{
//存放的R值就是角点分数,当R值很大的时候,就可以认为这个点是一个角点
int rsp = dst_norm.at<uchar>(i, j);
//当大于这个阈值分数的都可以判定为角点
if (rsp > thresh) {
int b = rng.uniform(0, 256);
int g = rng.uniform(0, 256);
int r = rng.uniform(0, 256);
circle(src_cornerHarris, Point(j, i), 5, Scalar(b, g, r), 2);
}
}
}
namedWindow(dst_name, WINDOW_AUTOSIZE);
imshow(dst_name, src_cornerHarris);
}
int main(){
src_cornerHarris=imread("D:/test/src9102.PNG");
copySrc = src_cornerHarris.clone();
if (src_cornerHarris.empty())
{
cout << "src is error" << endl;
return -1;
}
namedWindow(src_name, WINDOW_AUTOSIZE);
createTrackbar("Threshold:", src_name, &thresh, max_thresh, cornerHarrisTest);
imshow(src_name, src_cornerHarris);
cornerHarrisTest(0,0);
waitKey(0);
return 0;
}
3. Python实现
import cv2 as cv
import numpy as np
def cornerHarrisTest(src, opt=1):
blockSize = 2
apertureSize = 3
k = 0.04
gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
dst = cv.cornerHarris(gray, blockSize, apertureSize, k)
# normalize
dst_norm = np.empty(dst.shape, dtype=np.float32)
cv.normalize(dst, dst_norm, alpha=0, beta=255, norm_type=cv.NORM_MINMAX)
dst_norm_scale = cv.convertScaleAbs(dst_norm)
# draw circle
for i in range(dst_norm_scale.shape[0]):
for j in range(dst_norm_scale.shape[1]):
if int(dst_norm_scale[i, j]) > 97:
cv.circle(src, (j, i), 3, (0, 0, 255), 3)
return src
srcHarris = cv.imread("D:/test/src9102.PNG")
cv.imshow("src", srcHarris)
result = cornerHarrisTest(srcHarris)
cv.imshow("dst", result)
cv.waitKey(0)
cv.destroyAllWindows()
学习:
Harris 角点检测子
OpenCV图像处理- 角点检测
OpenCV之角点检测 – Harris角点检测
cv2.cornerHarris()详解 python+OpenCV 中的 Harris 角点检测
Harris角点算法
OpenCV——角点检测原理分析(Harris,Shi-Tomasi、亚像素级角点检测)