Python基础----NumPy
文章目录
- NumPy - 简介
- NumPy 操作
- 1、创建ndarray数组
- 1.1、基本的ndarray是使用 NumPy 中的数组函数创建
- 1.2、其他创建方法说明
- 1.3、numpy中的随机数生成
- 1.4、numpy.linspace使用详解
- 1.5、数组的元素重复操作
- 2、ndarray数组的操作
- 2.1、索引和切片
- 2.2、ndarray数组的转置和轴对换
- 2.3、ndarray数组的拆分与合并
- 2.4、ndarray数组重塑
- 2.5、ndarray数组的去重
- 2.6、numpy.where() 用法详解
- 3、数组的算数和逻辑运算
- 3.1、实例属性和方法
- 3.2、一元ufunc
- 3.3、多元ufunc
- 3.4、np.multiply()、np.dot()和星号(*)三种乘法运算的区别
- 4、numpy线性代数有关的操作
- 4.1、矩阵的转置
- 4.2、方阵的迹:方阵的迹就是主对角元素之和,使用trace()函数获得方阵的迹
- 4.3、计算行列式:np.linalg.det(A)
- 4.4、逆矩阵/伴随矩阵:若A存在逆矩阵(满足det(A) != 0,或者A满秩),使用linalg.inv求得方阵A的逆矩阵
- 4.5、解一元线性方程:使用np.linalg.solve()解一元线性方程组
- 4.6、计算矩阵距离:矩阵的距离,这里是的是欧几里得距离,说一下如何计算两个形状相同矩阵之间的距离
- 4.7、矩阵的秩:linalg.matrix_rank方法计算矩阵的秩
- 4.8、求方阵的特征值特征向量:a,b = np.linalg.eig(x)#特征值保存在a中,特征向量保存在b中
- 4.9、判断正定矩阵
NumPy - 简介
NumPy 是一个 Python 包。 它代表 “Numeric Python”。 它是一个由多维数组对象和用于处理数组的例程集合组成的库。
NumPy 操作
使用NumPy,开发人员可以执行以下操作:
- 数组的算数和逻辑运算。
- 与线性代数有关的操作。
- 傅立叶变换和用于图形操作的例程。
1、创建ndarray数组
1.1、基本的ndarray是使用 NumPy 中的数组函数创建
numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)
| 参数 | 说明 |
|---|---|
| object | 任何暴露数组接口方法的对象都会返回一个数组或任何(嵌套)序列。 |
| dtype | 数组的所需数据类型,可选。 |
| copy | 可选,默认为true,对象是否被复制。 |
| order | 按照C语言的行优先’C’,还是按照Fortran形式的列优先‘F’或A(任意,默认)存储在内存中 |
| subok | 默认情况下,返回的数组被强制为基类数组。 如果为true,则返回子类。 |
| ndimin | 指定返回数组的最小维数。 |
1.2、其他创建方法说明
| 方法 | 说明 |
|---|---|
| np.arange | 类似于内置的range,但返回的是ndarray不是list |
| np.zeros | 根据指定形状和数据类型创建一个全0数组 |
| np.ones | 根据指定形状和数据类型创建一个全1数组 |
| np.empty | 创建一个新数组,只分配内存空间但不填充任何值 |
| np.identity(n,dtype=None) | 创建一个正方的N*N方正,对角线为1,其他全为0 |
| np.eye | 默认参数为创建一个正方的N*N方正,对角线为1,其他全为0 |
np.eye(N,M=None,k=0,dtype=
| 参数 | 说明 |
|---|---|
| N | int型,表示的是输出的行数 |
| M | int型,可选项,输出的列数,如果没有就默认为N |
| k | int型,可选项,对角线的下标,默认为0表示的是主对角线,负数表示的是低对角,正数表示的是高对角。 |
| dtype | 数据的类型,可选项,返回的数据的数据类型 |
| order | {‘C’,‘F’},可选项,也就是输出的数组的形式是按照C语言的行优先’C’,还是按照Fortran形式的列优先‘F’存储在内存中 |
import numpy as np
print (np.version.version)
1.15.0
n1 = np.array([1,2,3])
print (n1)
print (n1.dtype,'\n',type(n1))
n2 = np.arange(10)
print (n2)
print (type(n2))
n3 = np.zeros((3,2),dtype= 'i8')
print (n3)
n4 = np.ones((2,3),dtype= 'i2')
print (n4)
n5 = np.empty((2,2))
print (n5.dtype,type(n5))
n6 = np.identity(3)
print (n6)
[1 2 3]
int32
[0 1 2 3 4 5 6 7 8 9]
[[0 0]
[0 0]
[0 0]]
[[1 1 1]
[1 1 1]]
float64
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
# np.eye与np.identity的区别
n7 = np.eye(3)
print (n7)
n71 = np.eye(3,2)
print (n71)
n72 = np.eye(3,k=-1)
print (n72)
n73 = np.eye(3,k=1)
print (n73)
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
[[1. 0.]
[0. 1.]
[0. 0.]]
[[0. 0. 0.]
[1. 0. 0.]
[0. 1. 0.]]
[[0. 1. 0.]
[0. 0. 1.]
[0. 0. 0.]]
指定ndarray数组元素的类型
| 类型 | 类型代码 | 说明 |
|---|---|---|
| int8、uint8 | i1、u1 | 有符号和无符号8位整型(1字节) |
| int16、uint16 | i2、u2 | 有符号和无符号16位整型(2字节) |
| int32、uint32 | i4、u4 | 有符号和无符号32位整型(4字节) |
| int64、uint64 | i8、u8 | 有符号和无符号64位整型(8字节) |
| float16 | f2 | 半精度浮点数 |
| float32 | f4、f | 单精度浮点数 |
| float64 | f8、d | 双精度浮点数 |
| float128 | f16、g | 扩展精度浮点数 |
| complex64 | c8 | 分别用两个32位表示的复数 |
| complex128 | c16 | 分别用两个64位表示的复数 |
| complex256 | c32 | 分别用两个128位表示的复数 |
| bool | ? | 布尔型 |
| object | O | python对象 |
| string | Sn | 固定长度字符串,每个字符1字节,如S10 |
| unicode | Un | 固定长度Unicode,字节数由系统决定,如U10 |
n1 = np.array([1,2,3],dtype = np.float64)
print (n1)
n11 = np.array([1,2,3],dtype = 'f8')
print (n11)
n2 = np.array([1,2,3],dtype = 'c8')
print (n2)
[1. 2. 3.]
[1. 2. 3.]
[1.+0.j 2.+0.j 3.+0.j]
1.3、numpy中的随机数生成
| 函数 | 说明 |
|---|---|
| np.random.seed() | 确定随机数生成种子 |
| np.random.seed(int) | 确定随机数生成种子 |
| np.random.seed(ndarray) | 确定随机数生成种子 |
| np.random.permutation(int) | 返回一个一维arange(int)的序列的随机排列 |
| np.random.permutation(ndarray) | 返回一个序列的随机排列 |
| np.random.shuffle(ndarray) | 对一个序列就地随机排列 |
| np.random.rand(d0,d1,…,dn) | 根据给定维度生成[0,1)之间的均匀数据,包含0,不包含1 |
| np.random.randint(begin,end,num=1) | 从给定的begin和end随机选取num个整数 |
| np.random.randn(N, M, …) | 生成一个NM…的正态分布(平均值为0,标准差为1)的ndarray |
| numpy.random.normal(loc=0,scale=1e-2,size=shape) | 生成一个大小size,均值loc,标准差scale的正态(高斯)分布的ndarray |
| numpy.random.uniform(low,high,size) | 从一个均匀分布[low,high)中随机采样size大小的ndarray |
permutation与shuffle比较,在达到 10^9级别以前,两者速度几乎没有差别,但是在 达到 10^9 以后两者速度差距明显拉大,shuffle 的用时明显短于 permutation。
所以在 array 很大的时候还是使用 shuffle 速度更快些,但要注意其不返回打乱后的 array,是 inplace 修改
np.random.seed(0)
n1 = np.random.permutation(16)
print (n1)
n2 = np.random.permutation(n1)
print (n2)
n3 = np.random.shuffle(n1)
print (n3)
print (n1)
'''
shuffle 速度更快些,但要注意其不返回打乱后的 array,是 inplace 修改
'''
n4 = np.random.rand(5)
print (n4)
n41 = np.random.rand(2,3)
print (n41)
n5 = np.random.randint(2,6,3)
print (n5)
n6 = np.random.randn(3,4)
print (n6)
n7 = np.random.uniform(3,6,(2,3))
print (n7)
[ 1 6 8 9 13 4 2 14 10 7 15 11 3 0 5 12]
[ 8 5 3 7 1 9 13 15 11 4 12 10 0 14 2 6]
None
[ 4 0 14 13 15 5 2 11 7 3 6 10 9 8 1 12]
[0.75861562 0.10590761 0.47360042 0.18633234 0.73691818]
[[0.21655035 0.13521817 0.32414101]
[0.14967487 0.22232139 0.38648898]]
[2 3 4]
[[-0.88778575 -1.98079647 -0.34791215 0.15634897]
[ 1.23029068 1.20237985 -0.38732682 -0.30230275]
[-1.04855297 -1.42001794 -1.70627019 1.9507754 ]]
[[5.96512151 3.30613443 3.62663027]
[3.48392855 4.95932498 3.75987481]]
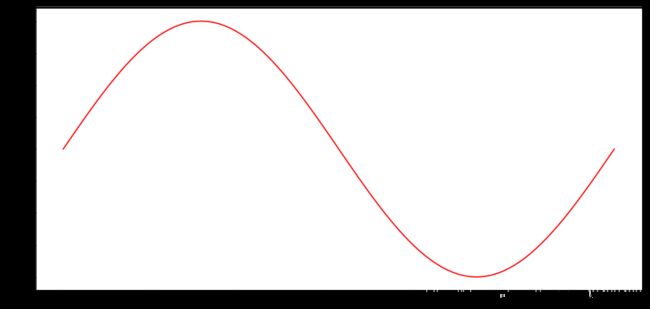
1.4、numpy.linspace使用详解
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
在指定的间隔内返回均匀间隔的数字。返回num均匀分布的样本,在[start, stop]。
from numpy import pi
x = np.linspace(0, 2*pi, 100)
print(x)
print ('*-'*40)
y = np.sin(np.linspace(0, 2*pi, 100))
print (y)
[0. 0.06346652 0.12693304 0.19039955 0.25386607 0.31733259
0.38079911 0.44426563 0.50773215 0.57119866 0.63466518 0.6981317
0.76159822 0.82506474 0.88853126 0.95199777 1.01546429 1.07893081
1.14239733 1.20586385 1.26933037 1.33279688 1.3962634 1.45972992
1.52319644 1.58666296 1.65012947 1.71359599 1.77706251 1.84052903
1.90399555 1.96746207 2.03092858 2.0943951 2.15786162 2.22132814
2.28479466 2.34826118 2.41172769 2.47519421 2.53866073 2.60212725
2.66559377 2.72906028 2.7925268 2.85599332 2.91945984 2.98292636
3.04639288 3.10985939 3.17332591 3.23679243 3.30025895 3.36372547
3.42719199 3.4906585 3.55412502 3.61759154 3.68105806 3.74452458
3.8079911 3.87145761 3.93492413 3.99839065 4.06185717 4.12532369
4.1887902 4.25225672 4.31572324 4.37918976 4.44265628 4.5061228
4.56958931 4.63305583 4.69652235 4.75998887 4.82345539 4.88692191
4.95038842 5.01385494 5.07732146 5.14078798 5.2042545 5.26772102
5.33118753 5.39465405 5.45812057 5.52158709 5.58505361 5.64852012
5.71198664 5.77545316 5.83891968 5.9023862 5.96585272 6.02931923
6.09278575 6.15625227 6.21971879 6.28318531]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[ 0.00000000e+00 6.34239197e-02 1.26592454e-01 1.89251244e-01
2.51147987e-01 3.12033446e-01 3.71662456e-01 4.29794912e-01
4.86196736e-01 5.40640817e-01 5.92907929e-01 6.42787610e-01
6.90079011e-01 7.34591709e-01 7.76146464e-01 8.14575952e-01
8.49725430e-01 8.81453363e-01 9.09631995e-01 9.34147860e-01
9.54902241e-01 9.71811568e-01 9.84807753e-01 9.93838464e-01
9.98867339e-01 9.99874128e-01 9.96854776e-01 9.89821442e-01
9.78802446e-01 9.63842159e-01 9.45000819e-01 9.22354294e-01
8.95993774e-01 8.66025404e-01 8.32569855e-01 7.95761841e-01
7.55749574e-01 7.12694171e-01 6.66769001e-01 6.18158986e-01
5.67059864e-01 5.13677392e-01 4.58226522e-01 4.00930535e-01
3.42020143e-01 2.81732557e-01 2.20310533e-01 1.58001396e-01
9.50560433e-02 3.17279335e-02 -3.17279335e-02 -9.50560433e-02
-1.58001396e-01 -2.20310533e-01 -2.81732557e-01 -3.42020143e-01
-4.00930535e-01 -4.58226522e-01 -5.13677392e-01 -5.67059864e-01
-6.18158986e-01 -6.66769001e-01 -7.12694171e-01 -7.55749574e-01
-7.95761841e-01 -8.32569855e-01 -8.66025404e-01 -8.95993774e-01
-9.22354294e-01 -9.45000819e-01 -9.63842159e-01 -9.78802446e-01
-9.89821442e-01 -9.96854776e-01 -9.99874128e-01 -9.98867339e-01
-9.93838464e-01 -9.84807753e-01 -9.71811568e-01 -9.54902241e-01
-9.34147860e-01 -9.09631995e-01 -8.81453363e-01 -8.49725430e-01
-8.14575952e-01 -7.76146464e-01 -7.34591709e-01 -6.90079011e-01
-6.42787610e-01 -5.92907929e-01 -5.40640817e-01 -4.86196736e-01
-4.29794912e-01 -3.71662456e-01 -3.12033446e-01 -2.51147987e-01
-1.89251244e-01 -1.26592454e-01 -6.34239197e-02 -2.44929360e-16]
import matplotlib.pyplot as plt
plt.figure
plt.figure(figsize = (30,6.5))
plt.subplot(1,2,1)
plt.plot(x,y,'r');
1.5、数组的元素重复操作
arr1.repeat、np.tile
print ('数组的元素重复操作:')
x = np.array([[1,2],[3,4]])
print (x.repeat(2)) # 按元素重复
print (x.repeat(2,axis=0)) # 按行重复
print (x.repeat(2,axis=1)) # 按列重复
print ('*-'*20)
x = np.array([[1,2],[3,4]])
print (np.tile(x,2))
print (np.tile(x, (2, 1))) # 指定从低维到高维依次复制的次数。
数组的元素重复操作:
[1 1 2 2 3 3 4 4]
[[1 2]
[1 2]
[3 4]
[3 4]]
[[1 1 2 2]
[3 3 4 4]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[1 2 1 2]
[3 4 3 4]]
[[1 2]
[3 4]
[1 2]
[3 4]]
2、ndarray数组的操作
此处的操作不包含改变数组中的值大小,指改变形状大小,改变元素位置的一些列操作
2.1、索引和切片
-
一维数组的索引:与Python的列表索引功能相似
-
多维数组的索引:
arr[r1:r2, c1:c2]
arr[1,1] 等价 arr[1][1]
[:] 代表某个维度的数据
- 布尔索引:使用布尔数组作为索引。arr[condition],condition为一个条件/多个条件组成的布尔数组。
切片不会复制原数组,而是生成原数组的视图,对视图的更改会反映到原数组上。一般的函数都是直接在原数组上进行操作,这样不用复制数组,节省大量时间
n1 = np.arange(15).reshape(3,5)
print (n1)
n11 = n1[0:2,1:4]
print (n11) # 左开右闭区间
print ('*-'*20)
n11[1,2] = 6
print (n11)
print (n1)
print ('*-'*20)
print (n1[2,2],n1[2][2])
cd = np.array([True,False,True])
print (n1[cd])
cd1 = (n1 >= 5)
print (cd1)
print (n1[cd1])
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
[[1 2 3]
[6 7 8]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[1 2 3]
[6 7 6]]
[[ 0 1 2 3 4]
[ 5 6 7 6 9]
[10 11 12 13 14]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
12 12
[[ 0 1 2 3 4]
[10 11 12 13 14]]
[[False False False False False]
[ True True True True True]
[ True True True True True]]
[ 5 6 7 6 9 10 11 12 13 14]
2.2、ndarray数组的转置和轴对换
数组的转置/轴对换只会返回源数据的一个视图,不会对源数据进行修改
- 转置(矩阵)数组T
- 轴变换 transpose 参数:由轴编号组成的元组
- 轴交换 swapaxes (axes:轴),参数:一对轴编号
# 转置(矩阵)数组
n1 = np.arange(6).reshape(2,3)
print (n1)
print (n1.T)
print (np.dot(n1,n1.T))
n2 = np.arange(24).reshape(4,3,2)
print (n2)
print ('*-'*20)
print (n2[1,:,:])
print ('*-'*20)
print (n2[:,1,:])
print ('*-'*20)
print (n2[:,:,1])
# 轴变换 transpose
print ('*-'*20)
n3 = n2.transpose((1,0,2))
print (n3)
# 轴交换 swapaxes
print ('*-'*20)
n4 = n2.swapaxes(1,0)
print (n4)
[[0 1 2]
[3 4 5]]
[[0 3]
[1 4]
[2 5]]
[[ 5 14]
[14 50]]
[[[ 0 1]
[ 2 3]
[ 4 5]]
[[ 6 7]
[ 8 9]
[10 11]]
[[12 13]
[14 15]
[16 17]]
[[18 19]
[20 21]
[22 23]]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[ 6 7]
[ 8 9]
[10 11]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[ 2 3]
[ 8 9]
[14 15]
[20 21]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[ 1 3 5]
[ 7 9 11]
[13 15 17]
[19 21 23]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[[ 0 1]
[ 6 7]
[12 13]
[18 19]]
[[ 2 3]
[ 8 9]
[14 15]
[20 21]]
[[ 4 5]
[10 11]
[16 17]
[22 23]]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[[ 0 1]
[ 6 7]
[12 13]
[18 19]]
[[ 2 3]
[ 8 9]
[14 15]
[20 21]]
[[ 4 5]
[10 11]
[16 17]
[22 23]]]
2.3、ndarray数组的拆分与合并
| 函数 | 说明 |
|---|---|
| numpy.split(A,2,axis=1) | 对矩阵数组分割分成两块,axis=1是列分割,axis=0是行分割。等量分割,必须能整除 |
| numpy.hsplit(A,3) | 横向分割 对于多维,只分割最外维的,等量分割,必须能整除 |
| numpy.vsplit(A,3) | 纵向分割,等量分割,必须能整除 |
| numpy.dsplit() | 深度分割 |
| numpy.concatenate((A,B,B,A),axis=0) | 合并矩阵,axis=1表示水平合并,axis=0表示垂直合并 |
| numpy.hstack((A,B,C)) | 左右合并矩阵数组A,B,C |
| numpy.vstack((A,B,C)) | 上下合并矩阵数组A,B,C。 |
arr1 = np.arange(8).reshape(2,4)
print (arr1)
arr1_1,arr1_2 = np.split(arr1,2,axis=1)
print (arr1_1)
print (arr1_2)
arr2 = np.hsplit(arr1,2)
print (arr2)
arr3 = np.vsplit(arr1,2)
print (arr3)
print ('*-'*30)
arr4 = np.concatenate((arr1_1,arr1_2),axis = 1)
print (arr4)
arr41 = np.concatenate(arr2,axis = 1)
print (arr41)
print ('*-'*30)
arr5 = np.hstack(arr2)
print (arr5)
arr6 = np.vstack(arr3)
print (arr6)
[[0 1 2 3]
[4 5 6 7]]
[[0 1]
[4 5]]
[[2 3]
[6 7]]
[array([[0, 1],
[4, 5]]), array([[2, 3],
[6, 7]])]
[array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]])]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[0 1 2 3]
[4 5 6 7]]
[[0 1 2 3]
[4 5 6 7]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[0 1 2 3]
[4 5 6 7]]
[[0 1 2 3]
[4 5 6 7]]
2.4、ndarray数组重塑
| 函数 | 说明 |
|---|---|
| numpy.reshape(N,M) | 转换数组阵维数为N行M列 |
| numpy.ravel() | 输出一个多维数组被抹平成一维数组的视图 |
| ndarray.flatten() | 返回数组元素形成的列表,flat()返回迭代对象。 |
numpy.flatten()返回一份拷贝,对拷贝所做的修改不会影响(reflects)原始矩阵,而numpy.ravel()返回的是视图view,会影响(reflects)原始矩阵
arr1 = np.arange(6)
print (arr1)
arr2 = arr1.reshape(2,3)
print (arr2)
arr3 = arr1.ravel()
print (arr3)
arr4 = arr2.flatten()
print (arr4)
print ('*-'*20)
arr3[1] = 0
# arr3 和arr2 只是视图,若被修改都会被修改
print (arr4,type(arr4),id(arr4))
print (arr3,type(arr4),id(arr3))
print (arr2,type(arr2),id(arr2))
print (arr1,type(arr1),id(arr1))
[0 1 2 3 4 5]
[[0 1 2]
[3 4 5]]
[0 1 2 3 4 5]
[0 1 2 3 4 5]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[0 1 2 3 4 5] 1668353215664
[0 0 2 3 4 5] 1668353215344
[[0 0 2]
[3 4 5]] 1668361038544
[0 0 2 3 4 5] 1668357589152
2.5、ndarray数组的去重
去重np.unique(A, return_index=True, return_inverse=True)
| 函数 | 说明 |
|---|---|
| a = np.unique(A) | 对于一维数组或者列表,unique函数去除其中重复的元素,并返回一个新的无元素重复的列表 |
| return_index=True | 表示返回新列表元素在旧列表中的位置,并以列表形式储存 |
| return_inverse=True | 表示返回旧列表元素在新列表中的位置,并以列表形式储存 |
A = [1, 2, 2, 5,3, 4, 3,5]
a = np.unique(A)
B= (1, 2, 2,5, 3, 4, 3,5)
b= np.unique(B)
print (a,type(a))
print (b)
print ('*-'*20)
_,d,e = np.unique(A, return_index=True, return_inverse=True)
print (d)
print (e)
print ('*-'*20)
arr1 = np.array(A).reshape(2,4)
print (arr1)
arr2,f,g = np.unique(arr1, return_index=True, return_inverse=True)
print (arr2,type(arr1))
print (f)
print (g)
[1 2 3 4 5]
[1 2 3 4 5]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[0 1 4 5 3]
[0 1 1 4 2 3 2 4]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[1 2 2 5]
[3 4 3 5]]
[1 2 3 4 5]
[0 1 4 5 3]
[0 1 1 4 2 3 2 4]
2.6、numpy.where() 用法详解
np.where(condition, x, y),第一个参数为一个布尔数组,第二个参数和第三个参数可以是标量也可以是数组
numpy.where() 有两种用法:
-
np.where(condition, x, y)满足条件(condition),输出x,不满足输出y
-
np.where(condition)只有条件 (condition),没有x和y,则输出满足条件 (即非0) 元素的坐标
arr1 = np.arange(10)
arr2 = np.where(arr1 > 5,1,-1)
print (arr2)
arr3 = np.where(arr1 > 5)
print (arr3)
print ('*-'*20)
print ('where函数的嵌套使用')
y1 = np.array([-1,-2,-3,-4,-5,-6])
y2 = np.array([1,2,3,4,5,6])
y3 = np.zeros(6)
cond = np.array([1,2,3,4,5,6])
x = np.where(cond>5,y3,np.where(cond>2,y1,y2))
print (x)
[-1 -1 -1 -1 -1 -1 1 1 1 1]
(array([6, 7, 8, 9], dtype=int64),)
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
where函数的嵌套使用
[ 1. 2. -3. -4. -5. 0.]
3、数组的算数和逻辑运算
3.1、实例属性和方法
| 函数 | 说明 |
|---|---|
| ndarray.astype(dtype) | 转换类型,若转换失败则会出现TypeError |
| ndarray.copy() | 复制一份ndarray(新的内存空间) |
| ndarray.reshape((N,M,…)) | 将ndarray转化为N X M…的多维ndarray(非copy) |
| ndarray.transpose((xIndex,yIndex,…)) | 根据维索引xIndex,yIndex…进行矩阵转置,依赖于shape,不能用于一维矩阵(非copy) |
| ndarray.swapaxes(xIndex,yIndex) | 交换维度(非copy) |
| ndarray.mean( axis=0 ) | 求平均值 |
| ndarray.sum( axis= 0) | 求和 |
| ndarray.cumsum( axis=0) | 累加 |
| ndarray.cumprod( axis=0) | 累乘 |
| ndarray.std() | 标准差 |
| ndarray.var() | 方差 |
| ndarray.max() | 最大值 |
| ndarray.min() | 最小值 |
| ndarray.argmax() | 最大值索引 |
| ndarray.argmin() | 最小值索引 |
| ndarray.any() | 是否至少有一个True |
| ndarray.all() | 是否全部为True |
| ndarray.dot( ndarray) | 计算矩阵内积 |
| ndarray.sort(axis=0) | 排序,返回源数据 |
arr1 = np.array([1,2,3,4])
print (arr1.dtype)
arr11 = arr1.astype(np.float32)
print (arr11.dtype)
arr2 = arr11.copy()
print (id(arr11),id(arr2))
arr21 = arr2.reshape(2,2)
print (arr21)
print ('*-'*20)
arr3 = arr21.transpose(1,0)
print (arr3)
arr4 = arr21.swapaxes(1,0)
print (arr4)
arr3[1,1] = -1
print (arr21)
print ('arr4:')
print (arr4)
# transpose/swapaxes产生的只是视图
print ('*-'*20)
print (arr4.mean())
print (arr4.mean(axis=0))
print (arr4.sum())
print ('累加和累积:')
print (arr4.cumsum())
print (arr4.cumprod())
print ('*-'*20)
print ('标准差与方差:')
print (arr4.std())
print (arr4.var())
print (arr4.argmax())
print (arr4.argmin())
arr4.sort(axis=0)
print (arr4)
int32
float32
1668353214384 1668347963392
[[1. 2.]
[3. 4.]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[1. 3.]
[2. 4.]]
[[1. 3.]
[2. 4.]]
[[ 1. 2.]
[ 3. -1.]]
arr4:
[[ 1. 3.]
[ 2. -1.]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
1.25
[1.5 1. ]
5.0
累加和累积:
[1. 4. 6. 5.]
[ 1. 3. 6. -6.]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
标准差与方差:
1.47902
2.1875
1
3
[[ 1. -1.]
[ 2. 3.]]
ndarray通用函数,通用函数(ufunc)是一种对ndarray中的数据执行元素级运算的函数。
3.2、一元ufunc
| 函数 | 说明 |
|---|---|
| np.abs(ndarray) | 计算绝对值 |
| np.fabs(ndarray) | 计算绝对值(非复数) |
| np.mean(ndarray) | 求平均值 |
| np.sqrt(ndarray) | 计算x^0.5 |
| np.square(ndarray) | 计算x^2 |
| np.exp(ndarray) | 计算e^x |
| log、log10、log2、log1p | 计算自然对数、底为10的log、底为2的log、底为(1+x)的log |
| np.sign(ndarray) | 计算正负号:1(正)、0(0)、-1(负) |
| np.ceil(ndarray) | 计算大于等于该值的最小整数 |
| np.floor(ndarray) | 计算小于等于该值的最大整数 |
| np.rint(ndarray) | 四舍五入到最近的整数,保留dtype |
| np.modf(ndarray) | 将数组的小数和整数部分以两个独立的数组方式返回 |
| np.isnan(ndarray) | 返回一个判断是否是NaN的bool型数组 |
| np.isfinite(ndarray) | 返回一个判断是否是有穷(非inf,非NaN)的bool型数组 |
| np.isinf(ndarray) | 返回一个判断是否是无穷的bool型数组 |
| cos、cosh、sin、sinh、tan、tanh | 普通型和双曲型三角函数 |
| arccos、arccosh、arcsin、arcsinh、arctan、arctanh | 反三角函数和双曲型反三角函数 |
| np.logical_not(ndarray) | 计算各元素not x的真值,相当于-ndarray |
arr1 = np.array([[1,-3,4,-4],[2,4,-1,2]])
arr11 = np.abs(arr1)
print (arr11)
print (arr11.mean())
print (arr11.mean(axis=1))
print (arr11.mean(axis=0))
arr2 = np.square(arr1)
print (arr2)
arr21 = np.sqrt(arr2)
print (arr21)
print (np.exp(arr21))
arr3 = arr1/2
print (arr3)
# 将小数和整数拆分分别组成一个数组
arr31,arr32 = np.modf(arr3)
print (arr31)
print (arr32)
print ('*-'*20)
arr4 = arr1/4
print (arr4)
arr41 = np.arccos(arr4)
print (arr41)
arr42 = np.cos(arr41)
print (arr42)
print (np.logical_not(arr42==1))
print (np.isfinite(arr42))
[[1 3 4 4]
[2 4 1 2]]
2.625
[3. 2.25]
[1.5 3.5 2.5 3. ]
[[ 1 9 16 16]
[ 4 16 1 4]]
[[1. 3. 4. 4.]
[2. 4. 1. 2.]]
[[ 2.71828183 20.08553692 54.59815003 54.59815003]
[ 7.3890561 54.59815003 2.71828183 7.3890561 ]]
[[ 0.5 -1.5 2. -2. ]
[ 1. 2. -0.5 1. ]]
[[ 0.5 -0.5 0. -0. ]
[ 0. 0. -0.5 0. ]]
[[ 0. -1. 2. -2.]
[ 1. 2. -0. 1.]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[ 0.25 -0.75 1. -1. ]
[ 0.5 1. -0.25 0.5 ]]
[[1.31811607 2.41885841 0. 3.14159265]
[1.04719755 0. 1.82347658 1.04719755]]
[[ 0.25 -0.75 1. -1. ]
[ 0.5 1. -0.25 0.5 ]]
[[ True True False True]
[ True False True True]]
[[ True True True True]
[ True True True True]]
3.3、多元ufunc
| 函数 | 说明 |
|---|---|
| np.add(ndarray, ndarray) | 相加 |
| np.subtract(ndarray, ndarray) | 相减 |
| np.multiply(ndarray, ndarray) | 乘法 |
| np.divide(ndarray, ndarray) | 除法 |
| np.floor_divide(ndarray, ndarray) | 圆整除法(丢弃余数) |
| np.power(ndarray, ndarray) | 次方 |
| np.mod(ndarray, ndarray) | 求模 |
| np.maximum(ndarray, ndarray) | 求最大值 |
| np.fmax(ndarray, ndarray) | 求最大值(忽略NaN) |
| np.minimun(ndarray, ndarray) | 求最小值 |
| np.fmin(ndarray, ndarray) | 求最小值(忽略NaN) |
| np.copysign(ndarray, ndarray) | 将参数2中的符号赋予参数1 |
| np.greater(ndarray, ndarray) | > |
| np.greater_equal(ndarray, ndarray) | >= |
| np.less(ndarray, ndarray) | < |
| np.less_equal(ndarray, ndarray) | <= |
| np.equal(ndarray, ndarray) | == |
| np.not_equal(ndarray, ndarray) | != |
| logical_and(ndarray, ndarray) | & |
| logical_or(ndarray, ndarray) | |
| logical_xor(ndarray, ndarray) | ^ |
| np.dot( ndarray, ndarray) | 计算两个ndarray的矩阵内积 |
arr1 = np.array([[9,8],[7,6]])
arr2 = np.array([[1,2],[3,4]])
arr12 = np.add(arr1,arr2)
print (arr12)
arr3 = np.subtract(arr12 ,arr2)
print (arr3)
arr4 = np.multiply(arr1,arr2)
print (arr4)
arr5 = np.divide(arr4,arr1)
print (arr5)
print (np.floor_divide(arr1,arr2))
print (np.power(arr1,arr2))
print ('求模与矩阵内积:')
print (np.mod(arr1,arr2))
print (np.dot(arr1,arr2))
[[10 10]
[10 10]]
[[9 8]
[7 6]]
[[ 9 16]
[21 24]]
[[1. 2.]
[3. 4.]]
[[9 4]
[2 1]]
[[ 9 64]
[ 343 1296]]
求模与矩阵内积:
[[0 0]
[1 2]]
[[33 50]
[25 38]]
3.4、np.multiply()、np.dot()和星号(*)三种乘法运算的区别
3.4.1、np.multiply()函数:
数组和矩阵对应位置相乘,输出与相乘数组/矩阵的大小一致
3.4.2、np.dot()函数:
数组场景
- 对于秩为1的数组,执行对应位置相乘,然后再相加;
- 对于秩不为1的二维数组,执行矩阵乘法运算;
矩阵场景
np.dot(np.mat(A),np.mat(B)),执行矩阵乘法运算
3.4.3、星号(*)乘法运算:
对数组执行对应位置相乘,对矩阵执行矩阵乘法运算
np.random.seed(41)
a = np.arange(1,5).reshape(2,2)
print (a,type(a))
A = np.mat(a)
print (A,type(A))
b = np.random.randint(1,5,(2,2))
print (b)
B = np.mat(b)
print ('*-'*20)
print (np.multiply(a,b))
print (np.multiply(A,B))
[[1 2]
[3 4]]
[[1 2]
[3 4]]
[[1 4]
[1 3]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[ 1 8]
[ 3 12]]
[[ 1 8]
[ 3 12]]
print (np.dot(a,b))
print (np.dot(A,B))
a1 = np.array([2,3])
b1 = np.array([3,4])
print (np.dot(a1,b1))
print (a*b)
print (A*B)
[[ 3 10]
[ 7 24]]
[[ 3 10]
[ 7 24]]
18
[[ 1 8]
[ 3 12]]
[[ 3 10]
[ 7 24]]
4、numpy线性代数有关的操作
4.1、矩阵的转置
- 验证矩阵转置的性质:(A±B)’=A’±B’
- 验证矩阵转置的性质:(KA)’=KA’
- 验证矩阵转置的性质:(A×B)’= B’×A’
import numpy.linalg as nla
np.random.seed(3)
a = np.random.randint(1,5,(2,2))
print (a)
print (a.T)
print (a.T.T)
b = np.random.randint(3,8,(2,2))
print (b)
print ('*-'*20)
print ((a + b).T)
print (a.T + b.T)
print ('*-'*20)
print ((10*a).T)
print (10*a.T)
print ('*-'*20)
print ((a*b).T)
print (b.T * a.T)
[[3 1]
[2 4]]
[[3 2]
[1 4]]
[[3 1]
[2 4]]
[[3 3]
[3 6]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[ 6 5]
[ 4 10]]
[[ 6 5]
[ 4 10]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[30 20]
[10 40]]
[[30 20]
[10 40]]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[[ 9 6]
[ 3 24]]
[[ 9 6]
[ 3 24]]
4.2、方阵的迹:方阵的迹就是主对角元素之和,使用trace()函数获得方阵的迹
- A的迹等于A.T的迹
- 和的迹等于迹的和
print (np.trace(a + b))
print (np.trace(a) + np.trace(b))
16
16
4.3、计算行列式:np.linalg.det(A)
print (nla.det(a))
print (nla.det(b))
10.000000000000002
9.000000000000002
4.4、逆矩阵/伴随矩阵:若A存在逆矩阵(满足det(A) != 0,或者A满秩),使用linalg.inv求得方阵A的逆矩阵
- A_det = np.linalg.det(A) #求A的行列式,不为零则存在逆矩阵
- A_inverse = np.linalg.inv(A) #求A的逆矩阵
- np.dot(A, A_inverse) #A与其逆矩阵的乘积为单位阵
- A_companion = A_inverse * A_det #求A的伴随矩阵
a_inverse = nla.inv(a)
print (a_inverse)
print (np.dot(a,a_inverse))
# 伴随矩阵
a_companion = a_inverse * nla.det(a)
print (a_companion)
[[ 0.4 -0.1]
[-0.2 0.3]]
[[1. 0.]
[0. 1.]]
[[ 4. -1.]
[-2. 3.]]
4.5、解一元线性方程:使用np.linalg.solve()解一元线性方程组
np.allclose(a, b) 判断a,b两个矩阵是否相等
x + y - 3z = 8
2x - 3y + 4z = 20
-3x + 5y + z = 12
# 系数矩阵
A = np.array([[1,1,-3],[2,-3,4],[-3,5,1]])
print (A)
B = np.array([8,20,12])
print (B)
print ('*-'*20)
x = nla.solve(A, B)
print (x)
print (np.allclose(np.dot(A, x), B))
print (np.dot(A,x))
[[ 1 1 -3]
[ 2 -3 4]
[-3 5 1]]
[ 8 20 12]
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
[14.1 9.8 5.3]
True
[ 8. 20. 12.]
4.6、计算矩阵距离:矩阵的距离,这里是的是欧几里得距离,说一下如何计算两个形状相同矩阵之间的距离
np.random.seed(3)
a = np.random.randint(1,5,(2,2))
print (a)
b = np.random.randint(3,8,(2,2))
print (b)
# 距离矩阵c
c = a - b
print (c)
# 距离矩阵的平方
d = np.dot(c,c)
print (d)
# 计算矩阵的迹
e = np.trace(d)
print (e)
print (e**0.5)
[[3 1]
[2 4]]
[[3 3]
[3 6]]
[[ 0 -2]
[-1 -2]]
[[2 4]
[2 6]]
8
2.8284271247461903
4.7、矩阵的秩:linalg.matrix_rank方法计算矩阵的秩
arr1 = np.eye(4)
print (arr1)
print (nla.matrix_rank(arr1))
arr1[1,1] = 0
print (nla.matrix_rank(arr1))
[[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
4
3
4.8、求方阵的特征值特征向量:a,b = np.linalg.eig(x)#特征值保存在a中,特征向量保存在b中
- 根据公式 Ax = λx 检验特征值与特征向量是否正确
np.random.seed(3)
arr1 = np.diag((1, 2, 3))
print (arr1)
a,b = nla.eig(arr1) # 特征值保存在a中,特征向量保存在b中
print (a)
print (b)
print (nla.eigvals(arr1))
for i in range(3): # 方法一
if np.allclose(np.dot(a[i], b[:, i]), arr1[:, i]): # np.allclose()方法在第七节提到过
print ('Right')
else:
print ('Error')
for i in range(3): # 方法二
if (np.dot(a[i], b[:, i]) == arr1[:, i]).all():
print ('Right')
else:
print ('Error')
[[1 0 0]
[0 2 0]
[0 0 3]]
[1. 2. 3.]
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
[1. 2. 3.]
Right
Right
Right
Right
Right
Right
4.9、判断正定矩阵
- 设M是n阶方阵,如果对任何非零向量z,都有z’Mz> 0,其中z’ 表示z的转置,就称M正定矩阵。
判定定理1:对称阵A为正定的充分必要条件是:A的特征值全为正。
判定定理2:对称阵A为正定的充分必要条件是:A的各阶顺序主子式都为正。
判定定理3:任意阵A为正定的充分必要条件是:A合同于单位阵。
- 对对称阵进行cholesky分解,如果像这样没有提示出错,就说明它是正定的。如果提示出错,就说明它不是正定矩阵,你可以使用try函数捕获错误值
A = np.arange(16).reshape(4, 4)
# A = np.diag((1, 2, 3))
A = A + A.T
print (A)
try:
B = np.linalg.cholesky(A)
except :
print ('不是正定矩阵,不能进行cholesky分解。')
[[ 0 5 10 15]
[ 5 10 15 20]
[10 15 20 25]
[15 20 25 30]]
不是正定矩阵,不能进行cholesky分解。
内容有部分是参考以下2篇博客,非常感谢博主做的贡献:
https://blog.csdn.net/cxmscb/article/details/54583415#commentBox
https://blog.csdn.net/JavaMoo/article/details/77887141